Leetcode 119. Pascal's Triangle II (Easy)

이번 문제를 풀기 전에 118번 문제를 먼저 풀면 도움이 된다.

118번 문제는 아래 글에 정리해 놓았다.

 

https://coronasdk.tistory.com/1150

Leetcode 118. Pascal's Triangle (Easy)

Pascal's Triangle에 대한 패턴은 118번을 다룬 글에 정리해 두었다.

 

그 패턴들을 기반으로 구한 공식은 아래와 같다.

Triangle[row][col] = triangle[row-1][col-1] + triangle[row-1][col-1]

 

자세히 알기를 원하면 위에 있는 링크를 따라 가면 된다.

 

우선 이 결과를 얻으려면 아래와 같은 코딩으로 할 수 있다.

 

class Solution {
    
    private int getNum(int row, int col) {
        if(row == 0 || col == 0 || row == col) {
            return 1;
        }
        
        return getNum(row -1, col -1) + getNum(row-1, col);
    }
    
    public List<Integer> getRow(int rowIndex) {
        List<Integer> ans = new ArrayList<>();
        
        for(int i=0; i<= rowIndex; i++) {
            ans.add(getNum(rowIndex, i));
        }
        
        return ans;
    }
}

 

getNum() 메소드를 보면 첫번째 row 이거나 첫번째 col이거나 row와 col이 같다면 즉 맨 마지막 row 이면 값이 1이 주어진다.

getRow() 메소드에서 위 함수를 콜 한 부분을 보면 ans.add(getNum(rowIndex,i)); 이다.

즉 해당 값을 ans 에 넣는 것이다.

위에 설명한 1이 되는 경우 즉 맨 처음과 맨 마지막을 제외하면 getNum(row -1, col -1) + getNum(row-1, col) 로 계산된 값이 들어간다.

이는 재귀 함수 호출로 for 문과 같은 효과를 내는 방식인데 getNum() 함수 내에서 다시 getNum() 함수를 호출하는 방식이다.

 

이렇게 하면 원하는 답을 얻을 수 있다.

 

 

조금 다른 방법도 있다.

 

매번 재귀 함수를 호출하는 것이 아니라 이전에 호출했다 값은 미리 저장해 두고 계속 사용하는 것이다.

 

class Solution {
  private final class RowCol {
    private int row, col;

    public RowCol(int row, int col) {
      this.row = row;
      this.col = col;
    }

    @Override
    public int hashCode() {
      int result = (int) (row ^ (row >>> 32));
      return (result << 5) - 1 + (int) (col ^ (col >>> 32)); // 31 * result == (result << 5) - 1
    }

    @Override
    public boolean equals(Object o) {
      if (this == o) return true;
      if (o == null) return false;
      if (this.getClass() != o.getClass()) return false;

      RowCol rowCol = (RowCol) o;
      return row == rowCol.row && col == rowCol.col;
    }
  }

  private Map<RowCol, Integer> cache = new HashMap<>();

  private int getNum(int row, int col) {
    RowCol rowCol = new RowCol(row, col);

    if (cache.containsKey(rowCol)) {
      return cache.get(rowCol);
    }

    int computedVal =
        (row == 0 || col == 0 || row == col) ? 1 : getNum(row - 1, col - 1) + getNum(row - 1, col);

    cache.put(rowCol, computedVal);

    return computedVal;
  }

  public List<Integer> getRow(int rowIndex) {
    List<Integer> ans = new ArrayList<>();

    for (int i = 0; i <= rowIndex; i++) {
      ans.add(getNum(rowIndex, i));
    }

    return ans;
  }
}

 

But, it is worth noting that generating a number for a particular row requires only two numbers from the previous row. Consequently, generating a row only requires numbers from the previous row.

Thus, we could reduce our memory footprint by only keeping the latest row generated, and use that to generate a new row.

그러나 특정 행에 대한 숫자를 생성하려면 이전 행에서 두 개의 숫자만 필요하다는 점에 유의할 가치가 있습니다. 결과적으로 행을 생성하려면 이전 행의 숫자만 필요합니다.

따라서 생성된 최신 행만 유지하여 메모리 공간을 줄이고 이를 사용하여 새 행을 생성할 수 있습니다.

 

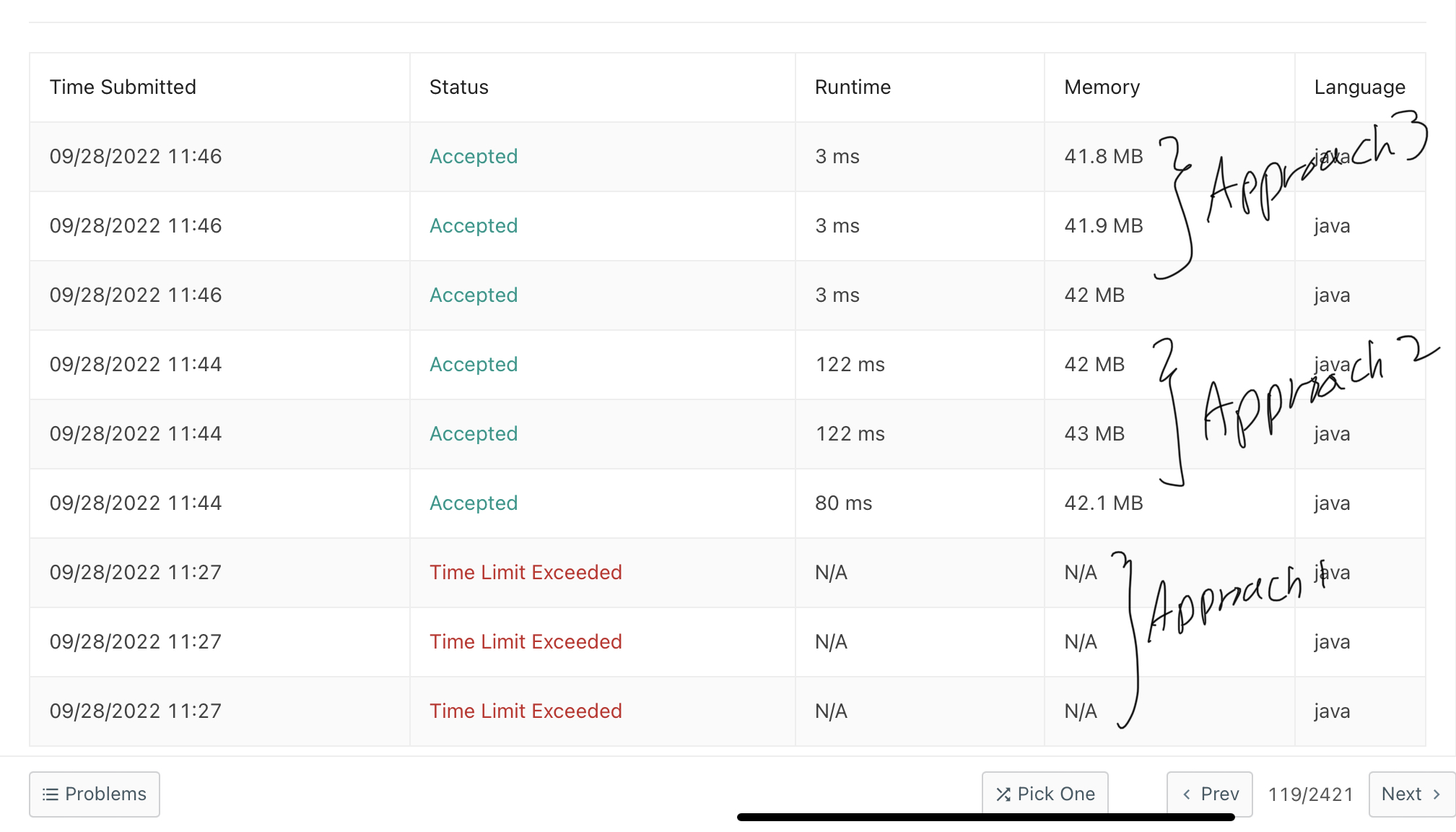
이 세가지 코드로 돌린 결과 입니다. 속도 면에서 아주 현격한 차이를 볼 수 있습니다.

 

이와는 아주 다른 접근법이 있을 수 있습니다.

이는 메모리를 절약할 수 있는 방법인데요.

 

여기서 행이 바뀔때마다 생기는 변화에 어떤 규칙성을 찾을 수 있습니다.

세번째줄 1,3,3,1에서 네번째 줄 1,4,6,4,1로 변화할 때의 규칙성을 보죠.

 

4번째 줄 맨 오른쪽은 1이 들어갑니다.

오른쪽에서 두번째 숫자는 3+1인 4가 됩니다.

그리고 오른쪽에서 세번째 숫자는 3+3 인 6이 됩니다. 오른쪽에서 네번째 숫자는 1+3인 4가 되구요. 

맨 왼쪽은 1이되구요.

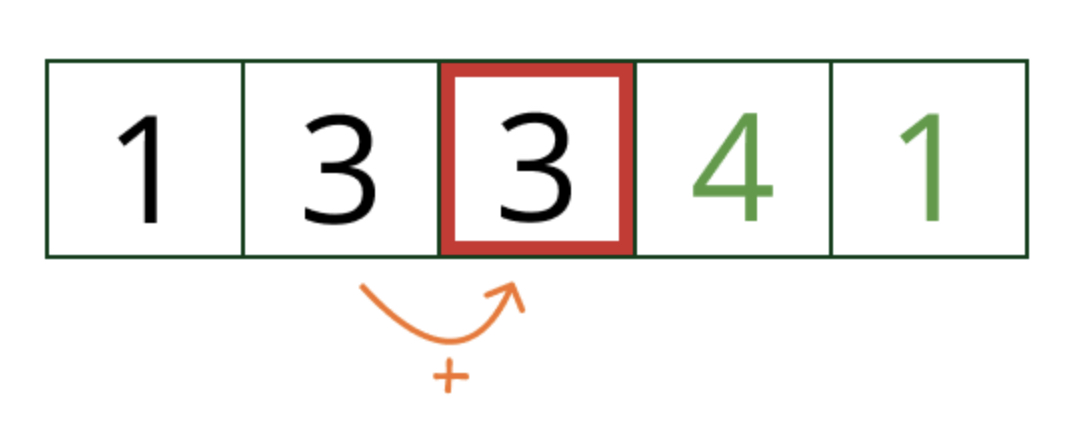
이 규칙을 가지고 코딩을 하면 아래와 같이 할 수 있습니다.

 

class Solution {
  public List<Integer> getRow(int rowIndex) {
    List<Integer> row =
        new ArrayList<>(rowIndex + 1) {
          {
            add(1);
          }
        };

    for (int i = 0; i < rowIndex; i++) {
      for (int j = i; j > 0; j--) {
        row.set(j, row.get(j) + row.get(j - 1));
      }
      row.add(1);
    }

    return row;
  }
}

 

그 다음은 수학인데요.

이 부분은 제가 잘 이해를 못했습니다.

 

소스 코드는 아래와 같구요.

 

class Solution {
  public List<Integer> getRow(int n) {
    List<Integer> row =
        new ArrayList<>() {
          {
            add(1);
          }
        };

    for (int k = 1; k <= n; k++) {
      row.add((int) ((row.get(row.size() - 1) * (long) (n - k + 1)) / k));
    }

    return row;
  }
}

 

실행 결과를 보면 아래와 같습니다.

 

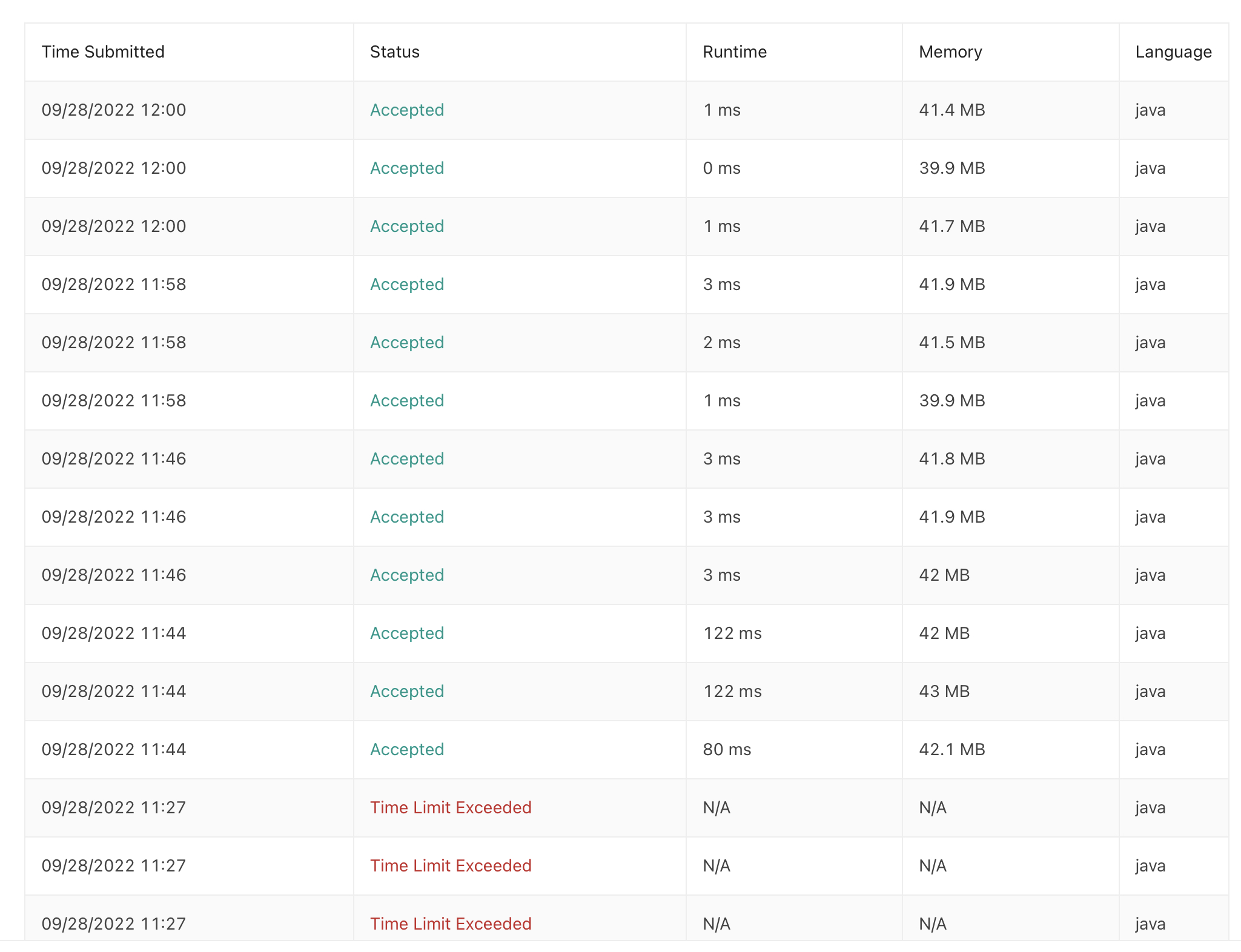
역시 수학 공식을 사용한 것이 Runtime과 메모리면에서 가장 효율적이네요.

 

20년동안 IT 분야에서 survival했지만 이렇게 까지 수학을 이용해서 코딩 해 본 적은 솔직히 없습니다.

 

좋은 걸 배웠지요.