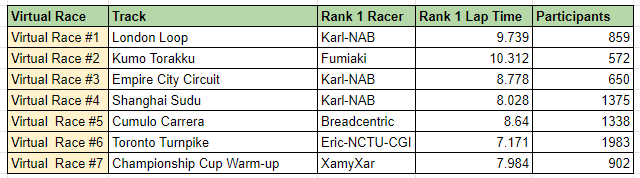
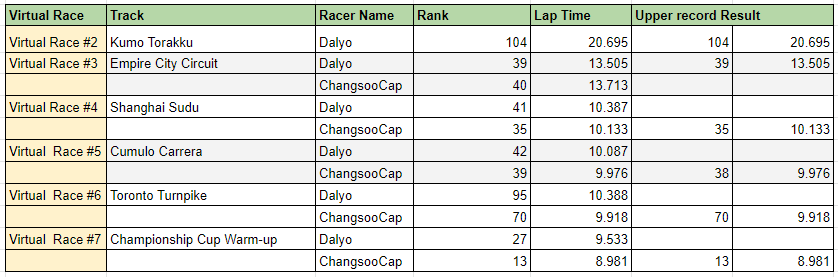
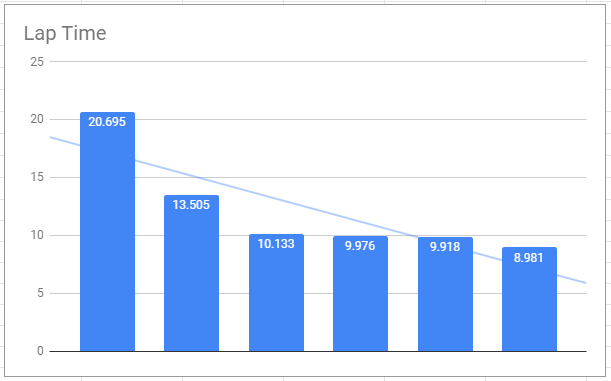
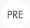Coursera에서 제공하는 Exam Prep: AWS Certified Solutions Architect-Associate 코스를 다 끝내고 테스트 문제를 풀었다.
총 31문제 중 첫번째 시도에서는 64.51점을 맞췄다.
두번째 시도에서는 90.32점.
세번째 시도에서야 100점을 맞았다.
왜 맞았는지, 왜 틀렸는지 찬찬히 한번 더 살펴봐야겠다.
Try again once you are ready
Grade received 64.51%
2nd Try
Your grade
90.32
3rd try
Grade received 100%
To pass 80% or higher
Benchmark Assessment
1.
Question 1
A company's application allows users to upload image files to an Amazon S3 bucket. These files are accessed frequently for the first 30 days. After 30 days, these files are rarely accessed, but need to be durably stored and available immediately upon request. A solutions architect is tasked with configuring a lifecycle policy that minimizes the overall cost while meeting the application requirements. Which action will accomplish this?
4.1 Identify cost-effective storage solutions
1 / 1 point
Configure a lifecycle policy to move the files to S3 Glacier after 30 days.
Configure a lifecycle policy to move the files to S3 Glacier Deep Archive after 30 days.
Configure a lifecycle policy to move the files to S3 Standard-Infrequent Access (S3 Standard-IA) after 30 days.
Configure a lifecycle policy to move the files to S3 One Zone-Infrequent Access (S3 One Zone-IA) after 30 days.
정답 3번
Correct
Correct. Using a lifecycle policy to move data to S3 Standard-IA satisfies all application requirements and provides the lowest-cost option. To learn more about S3 Standard-IA, see: Amazon S3 Storage Classes
Glacier는 available immediately라는 requirement를 충족할 수 없다..
S3 One Zone-IA는 to be durably stored 라는 requirement를 충족할 수 없다.
2.
Question 2
A company needs to implement a secure data encryption solution to meet regulatory requirements. The solution must provide security and durability in generating, storing, and controlling cryptographic data keys. Which action should be taken to provide the MOST secure solution?
3.3 Select appropriate data security options
1 / 1 point
Use AWS Key Management Service (AWS KMS) to generate AWS KMS keys and data keys. Use AWS KMS key policies to control access to the KMS keys.
Use AWS Key Management Service (AWS KMS) to generate cryptographic keys and import the keys to AWS Certificate Manager. Use IAM policies to control access to the keys.
Use a third-party solution from AWS Marketplace to generate the cryptographic keys and store them on encrypted instance store volumes. Use IAM policies to control access to the encryption key APIs.
Use OpenSSL to generate the cryptographic keys and upload the keys to an Amazon S3 bucket with encryption enabled. Apply AWS Key Management Service (AWS KMS) key policies to control access to the keys.
정답 1번
Correct
Correct. AWS KMS with customer controlled KMS keys meets all the requirements. To learn more about AWS KMS, see: AWS Key Management Service
AWS KMS를 사용하면 손쉽게 암호화 키를 생성 및 관리하고 다양한 AWS 서비스와 애플리케이션에서의 사용을 제어할 수 있다.
다른 보기들은 AWS KMS의 일체화된 서비스를 사용하는 것보다 secure 하지 않다.
3.
Question 3
A startup company is looking for a solution to cost-effectively run and access microservices without the operational overhead of managing infrastructure. The solution needs to be able scale quickly to accommodate rapid changes in the volume of requests and protect against common DDoS attacks. What is the MOST cost-effective solution that meets these requirements?
4.2 Identify cost-effective compute and database services
0 / 1 point
Run the microservices in containers using AWS Elastic Beanstalk.
Run the microservices in AWS Lambda behind an Amazon API Gateway.
Run the microservices on Amazon EC2 instances in an Auto Scaling group.
Run the microservices in containers using Amazon Elastic Container Service (Amazon ECS) backed by EC2 instances.
Incorrect
Incorrect. Amazon ECS is a highly scalable, fast, container management service that you can use to run, stop, and manage Docker containers on a cluster. However, you must manage the underlying EC2 instances unless you use AWS Fargate. Also, cluster scaling might not be fast enough to handle rapid changes in request volume. To learn more about Amazon ECS, see: What is Amazon Elastic Container Service?
ECS가 DDoS 공격도 관리할 줄 알았는데 아닌가 보다.
without operational overhead of managing infrastructure 가 있는거 보니 AWS Lambda 가 맞는것 같다.
Microservice는 소프트웨어가 잘 정의된API를 통해 통신하는 소규모의 독립적인 서비스로 구성되어 있는 경우의 소프트웨어 개발을 위한 아키텍처 및 조직적 접근 방식임. 독립적인 소규모 팀에서 보유 함.
정답 2번 – 두번째 시도에 맞춤
Correct
Correct. Lambda is a compute service that you can use to run code without provisioning or managing servers. Lambda runs code only when needed. It is a cost-effective solution because there is no charge for idle resources. To learn more about Lambda, see: What is AWS Lambda?
4.
Question 4
A solutions architect needs to design a secure environment for AWS resources that are being deployed to Amazon EC2 instances in a VPC. The solution should support for a three-tier architecture consisting of web servers, application servers, and a database cluster. The VPC needs to allow resources in the web tier to be accessible from the internet with only the HTTPS protocol. Which combination of actions would meet these requirements? (Select TWO.)
3.2 Design secure application tiers
1 / 1 point
Attach Amazon API Gateway to the VPC. Create private subnets for the web, application, and database tiers.
Private subnet을 적용하면 외부 접근이 안되서 Web은 Public을 해야 함.
Attach an internet gateway to the VPC. Create public subnets for the web tier. Create private subnets for the application and database tiers.
Correct
Correct. Only the web tier needs to be in public subnets. The application and database tiers should be in private subnets. To learn more about internet gateways, public subnets, and private subnets, see: VPCs and subnets
Attach a virtual private gateway to the VPC. Create public subnets for the web and application tiers. Create private subnets for the database tier.
application tier에 public을 적용할 필요가 없음. 비지니스 로직이 외부에 노출 될 우려가 있음
Create a web server security group that allows all traffic from the internet. Create an application server security group that allows requests from only the Amazon API Gateway on the application port. Create a database cluster security group that allows TCP connections from the application security group on the database port only.
Web server는 HTTPS 만 허용되어야 하기 때문에 requirement를 만족하지 못함.
Create a web server security group that allows HTTPS requests from the internet. Create an application server security group that allows requests from the web security group only. Create a database cluster security group that allows TCP connections from the application security group on the database port only.
정답 2, 5번
Correct
Correct. Putting the web tier in public subnets allows for greater access to the resource while protecting it from traffic on unrequired ports. Restricting traffic to the application and database tiers helps protect them from accidental and malicious access. It also helps ensure that each tier is accessed only through secure communication with the previous tier. To learn more about securing traffic in a VPC, see: Security groups for your VPC
5.
Question 5
A solutions architect has been given a large number of video files to upload to an Amazon S3 bucket. The file sizes are 100–500 MB. The solutions architect also wants to easily resume failed upload attempts. How should the solutions architect perform the uploads in the LEAST amount of time?
2.2 Select high-performing and scalable storage solutions for a workload
1 / 1 point
Split each file into 5-MB parts. Upload the individual parts normally and use S3 multipart upload to merge the parts into a complete object.
Using the AWS CLI, copy individual objects into the S3 bucket with the aws s3 cp command.
CLI를 사용하면 자동으로 multiuploading 기능을 제공 함
From the Amazon S3 console, select the S3 bucket. Upload the S3 bucket, and drag and drop items into the bucket.
Upload the files with SFTP and the AWS Transfer Family.
정답 2번
Correct
Correct. It is a best practice to use aws s3 commands (such as aws s3 cp) for multipart uploads and downloads. These aws s3 commands automatically perform multipart uploading and downloading based on the file size. To learn more about using the AWS CLI to perform multipart uploads, see: How do I use the AWS CLI to perform a multipart upload of a file to Amazon S3?
6.
Question 6
A gaming company is experiencing exponential growth. On multiple occasions, customers have been unable to access resources. To keep up with the increased demand, Management is considering deploying a cloud-based solution. The company is looking for a solution that can match the on-premises resilience of multiple data centers, and is robust enough to withstand the increased growth activity. Which configuration should a Solutions Architect implement to deliver the desired results?
1.2 Design highly available and/or fault-tolerant architectures
1 / 1 point
A VPC configured with an ELB Application Load Balancer targeting an EC2 Auto Scaling group consisting of Amazon EC2 instances in one Availability Zone è One AZ로는 fault-tolerant 를 보장할 수 없다.
Multiple Amazon EC2 instances configured within peered VPCs across two Availability Zones
A VPC configured with an ELB Network Load Balancer targeting an EC2 Auto Scaling group consisting of Amazon EC2 instances spanning two Availability Zones
Network LB는 다량의 request를 처리할 수 있다. Load balances at the transport layer (TCP/UDP Layer-4)
Network LB can handle traffic bursts, retain the source IP of the client and use a fixed IP for the life of the load balancer.
A VPC configured with an ELB Application Load Balancer targeting an EC2 Auto Scaling group consisting of Amazon EC2 instances spanning two AWS Regions
è load balances at the application layer (HTTP/HTTPS), path based routing.
정답 3번
Correct
Correct. The Network Load Balancer can handle millions of requests per second, while maintaining ultra-low latency. Combined with an Auto Scaling group, the Network Load Balancer can handle volatile traffic patterns. Setting the Auto Scaling group targets across multiple Availability Zones will make this highly available. To learn more about automatic scaling, see: Configure an Application Load Balancer or Network Load Balancer using the Amazon EC2 Auto Scaling console
7.
Question 7
A Solutions Architect must secure the network traffic for two applications running on separate Amazon EC2 instances in the same subnet. The applications are called Application A and Application B. Application A requires that inbound HTTP requests be allowed and all other inbound traffic be blocked. Application B requires that inbound HTTPS traffic be allowed and all other inbound traffic be blocked, including HTTP traffic. What should the Solutions Architect use to meet these requirements?
3.2 Design secure application tiers
0 / 1 point
Configure the access with network access control lists (network ACLs).
ACL은 subnet 단위에서 작용함. 두 EC2 instance들이 같은 subnet에 있기 때문에 이를 사용할 수 없다.
Configure the access with security groups. è 이게 답인가?
SG은 EC2 instance 단위로 적용 됨. Allow 만 허용되고 Deny는 설정 안 됨.
A security group acts as a virtual firewall, controlling the traffic that is allowed to reach and leave the resources that it is associated with. For example, after you associate a security group with an EC2 instance, it controls the inbound and outbound traffic for the instance.
Configure the network connectivity with VPC peering.
Region간 VPC를 프라이빗 주소(IPv4, IPv6)를 사용하여 라우팅 해 줌
Configure the network connectivity with route tables. è 두번째 시도 답 -틀림
The route table contains existing routes with targets other than a network interface, Gateway Load Balancer endpoint, or the default local route. The route table contains existing routes to CIDR blocks outside of the ranges in your VPC. Route propagation is enabled for the route table.
Incorrect
Incorrect. Though network ACLs can allow and block traffic, they operate at the subnet boundary. They use one set of rules for all traffic that enters or leaves a particular subnet. Because the EC2 instances for both applications are in the same subnet, they would use the same network ACL. However, the question requires different security requirements for each application. To learn more about securing traffic as it enters or leaves a subnet, see: Network ACLs
Incorrect
Incorrect. A route table contains a set of rules, called routes, that are used to determine where network traffic from your subnet or gateway is directed. It does not provide any ability to block traffic as requested for applications that are in the same subnet. To learn more about routing in Amazon VPC, see: Route tables for your VPC
두번째 시도 4번도 틀림
정답 2번
Correct
Correct. A security group acts as a virtual firewall for your instance to control inbound and outbound traffic. They support allow rules only, and they block all other traffic if a matching rule is not found. Security groups are applied specifically at the instance level, so different instances in the same subnet can have different rules applied to them. To learn more about securing traffic at the EC2 instance boundary, see: Security groups for your VPC
8.
Question 8
A data processing facility wants to move a group of Microsoft Windows servers to the AWS Cloud. Theses servers require access to a shared file system that can integrate with the facility's existing Active Directory infrastructure for file and folder permissions. The solution needs to provide seamless support for shared files with AWS and on-premises servers and allow the environment to be highly available. The chosen solution should provide added security by supporting encryption at rest and in transit. Which storage solution would meet these requirements?
4.1 Identify cost-effective storage solutions
0 / 1 point
An Amazon S3 File Gateway joined to the existing Active Directory domain
An Amazon FSx for the Windows File Server file system joined to the existing Active Directory domain
FSx for Windows File Server는 윈도우즈와 친화성이 매우 높다.
An Amazon Elastic File System (Amazon EFS) file system joined to an AWS Managed Microsoft AD domain
EFS는 리눅스 기반임
An Amazon S3 bucket mounted on Amazon EC2 instances in multiple Availability Zones running Windows Server
Incorrect
Incorrect. Amazon EFS is a scalable, elastic file system for Linux based workloads. It is not supported for the Windows based instances. To learn more about Amazon EFS, see: What is Amazon Elastic File System?
정답 2번 – 두번째 시도에 맞춤
Correct
Correct. Amazon FSx provides a fully managed native Microsoft Windows file system so you can easily move your Windows-based applications that require file storage to AWS. With Amazon FSx, there are no upfront hardware or software costs. You pay for only the resources used, with no minimum commitments, setup costs, or additional fees. To learn more about Amazon FSx, see: What is FSx for Windows File Server? To learn more about Using Microsoft Windows file shares, see: Using Microsoft Windows file shares
9.
Question 9
A Solutions Architect notices an abnormal amount of network traffic coming from an Amazon EC2 instance. The traffic is determined to be malicious and the destination needs to be determined. What tool can the Solutions Architect use to identify the destination of the malicious network traffic?
3.2 Design secure application tiers
1 / 1 point
Enable AWS CloudTrail and filter the logs.
Enable VPC Flow Logs and filter the logs.
Consult the AWS Personal Health Dashboard.
Filter the logs from Amazon CloudWatch.
정답 2번
Correct
Correct. VPC Flow Logs is a feature that you can use to capture information about the IP traffic going to and from network interfaces in a VPC. To learn more about flow log basics, see: VPC Flow Logs
10.
Question 10
A company is deploying an environment for a new data processing application. This application will be frequently accessed by 20 different departments across the globe seeking to run analytics. The company plans to charge each department for the cost of that department's access. Which solution will meet these requirements with the LEAST effort?
2.2 Select high-performing and scalable storage solutions for a workload
1 / 1 point
Amazon Aurora with global databases. Each department will query a database in a different Region, and the Region is tagged in the billing console.
PostgreSQL on Amazon RDS, with read replicas for each department. Each department will query the read replica tagged for their team in the billing console.
Amazon Redshift, with clusters set up for each department. Each department will query the cluster tagged for their team in the billing console.
Amazon Athena with workgroups set up for each department. Each department will query via the workgroup tagged for their team in the billing console.
정답 4번
Correct
Correct. Amazon Athena can query data in Amazon S3, and workgroups are purpose-built for cost allocation. For more information about Amazon Athena workgroups, see: Using Workgroups to Control Query Access and Costs
11.
Question 11
A company is migrating its on-premises application to Amazon Web Services and refactoring its design. The design will consist of frontend Amazon EC2 instances that receive requests, backend EC2 instances that process the requests, and a message queuing service to address decoupling the application. The Solutions Architect has been informed that a key aspect of the application is that requests are processed in the order in which they are received. Which AWS service should the Solutions Architect to decouple the application?
1.3 Design decoupling mechanisms using AWS services
1 / 1 point
Amazon Simple Queue Service (Amazon SQS) standard queue
Amazon Simple Notification Service (Amazon SNS)
Amazon Simple Queue Service (Amazon SQS) FIFO queue
Amazon Kinesis
정답 3번
Correct
Correct. Amazon SQS FIFO (First In First Out) queues process messages in the order they are received. To learn more about Amazon SQS queue types, see: Amazon SQS features
12.
Question 12
An API receives a high volume of sensor data. The data is written to a queue before being processed to produce trend analysis and forecasting reports. With the current architecture, some data records are being received and processed more than once. How can a solutions architect modify the architecture to ensure that duplicate records are not processed?
1.3 Design decoupling mechanisms using AWS services
1 / 1 point
Configure the API to send the records to Amazon Kinesis Data Streams.
Configure the API to send the records to Amazon Kinesis Data Firehose.
Configure the API to send the records to Amazon Simple Notification Service (Amazon SNS).
Configure the API to send the records to an Amazon Simple Queue Service (Amazon SQS) FIFO queue.
정답 4번
Correct
Correct: The FIFO queue improves on and complements the standard queue. The most important features of this queue type are FIFO (First-In-First-Out) delivery and exactly-once processing. The order that messages are sent and received in is strictly preserved. A message is delivered once, and remains available until a consumer processes and deletes it. Duplicates are not introduced into the FIFO queue. To learn more about Amazon SQS and FIFO queues, see: Message ordering
13.
Question 13
After reviewing the cost optimization checks in AWS Trusted Advisor, a team finds that it has 10,000 Amazon Elastic Block Store (Amazon EBS) snapshots in its account that are more than 30 days old. The team has determined that it needs to implement better governance for the lifecycle of its resources. Which actions should the team take to automate the lifecycle management of the EBS snapshots with the LEAST effort? (Select TWO.)
4.1 Identify cost-effective storage solutions
0 / 1 point
Create and schedule a backup plan with AWS Backup. è 이게 답인것 같음
AWS Backup을 사용하면 AWS 서비스 및 하이브리드 워크로드에서 데이터 보호를 중앙 집중화하고 자동화할 수 있습니다. AWS Backup은 정책을 기반으로 대규모 데이터 보호를 간편하고 비용 효율적으로 수행할 수 있는 완전관리형 서비스입니다.
Correct
Correct. The team wants to automate the lifecycle management of EBS snapshots. AWS Backup is a centralized backup service that automates backup processes for application data across AWS services in the AWS Cloud. It is designed to help you meet business and regulatory backup compliance requirements. AWS Backup provides a central place where you can configure and audit the AWS resources that you want to back up. You can also automate backup scheduling, set retention policies, and monitor all recent backup and restore activity. To learn more, see: What is AWS Backup?
Copy the EBS snapshots to Amazon S3, and then create lifecycle configurations in the S3 bucket.
좀 더 간단한 방법이 있다.
This should not be selected
Incorrect. Though this solution meets the technical requirement, it does not meet the requirement for the least effort. To copy EBS snapshots and set up lifecycle policies on the S3 bucket, the team would need to provide manual effort or create scripts that would need to be hosted somewhere. To learn more, see: Copy an Amazon EBS snapshot
Use Amazon Data Lifecycle Manager (Amazon DLM).
Correct
Correct. With Amazon DLM, you can manage the lifecycle of your AWS resources through lifecycle policies. Lifecycle policies automate operations on specified resources. The team requires lifecycle management for EBS snapshots, and Amazon DLM supports EBS volumes and snapshots. To learn more about Amazon DLM, see: Amazon Data Lifecycle Manager
Use a scheduled event in Amazon EventBridge (Amazon CloudWatch Events) and invoke AWS Step Functions to manage the snapshots.
Amazon EventBridge는 자체 애플리케이션, 통합 Software-as-a-Service(SaaS) 애플리케이션 및 AWS 서비스에서 생성된 이벤트를 사용하여 이벤트 기반 애플리케이션을 대규모로 손쉽게 구축할 수 있는 서버리스 이벤트 버스입니다.
Schedule and run backups in AWS Systems Manager.
정답 1,3 – 두번째 시도에 맞춤
14.
Question 14
A company is deploying a production portal application on AWS. The database tier runs on a MySQL database. The company requires a highly available database solution that maximizes ease of management. How can the company meet these requirements?
1.2 Design highly available and/or fault-tolerant architectures
1 / 1 point
Deploy the database on multiple Amazon EC2 instances that are backed by Amazon Elastic Block Store (Amazon EBS) across multiple Availability Zones. Schedule periodic EBS snapshots.
Use Amazon RDS with a Multi-AZ deployment. Schedule periodic database snapshots.
Use Amazon RDS with a Single-AZ deployment. Schedule periodic database snapshots.
Use Amazon DynamoDB with an Amazon DynamoDB Accelerator (DAX) cluster. Create periodic on-demand backups.
정답 2번
Correct
Correct. Amazon RDS with a Multi-AZ deployment provides automatic failover with minimum manual intervention and it is highly available. To learn more, see: High availability (Multi-AZ) for Amazon RDS
15.
Question 15
A company requires operating system permissions on a relational database server. What should a solutions architect suggest as a configuration for a highly available database architecture?
1.2 Design highly available and/or fault-tolerant architectures
0 / 1 point
Multiple Amazon EC2 instances in a database replication configuration that uses two Availability Zones è 이게 답인가?
A database installed on a single Amazon EC2 instance in an Availability Zone
Amazon RDS in a Multi-AZ configuration with Provisioned IOPS
Multiple Amazon EC2 instances in a replication configuration that uses a placement group
Incorrect
Incorrect. This solution meets the requirement for high availability, but it does not provide access to the operating system. To learn more about when to use EC2 instances, see: Amazon EC2 for Oracle - When to choose Amazon EC2
정답 1 – 두번째 시도에 맞춤
Correct
Correct. EC2 instances allow access to the operating system. In addition, spanning two Availability Zones helps ensure high availability. To learn more about best practices for databases, see: Web Application Hosting in the AWS Cloud
16.
Question 16
A company has developed an application that processes photos and videos. When users upload photos and videos, a job processes the files. The job can take up to 1 hour to process long videos. The company is using Amazon EC2 On-Demand Instances to run web servers and processing jobs. The web layer and the processing layer have instances that run in an Auto Scaling group behind an Application Load Balancer. During peak hours, users report that the application is slow and that the application does not process some requests at all. During evening hours, the systems are idle. What should a solutions architect do so that the application will process all jobs in the MOST cost-effective manner?
2.1 Identify elastic and scalable compute solutions for a workload
1 / 1 point
Use a larger instance size in the Auto Scaling groups of the web layer and the processing layer.
Use Spot Instances for the Auto Scaling groups of the web layer and the processing layer.
Use an Amazon Simple Queue Service (Amazon SQS) standard queue between the web layer and the processing layer. Use a custom queue metric to scale the Auto Scaling group in the processing layer.
Use AWS Lambda functions instead of EC2 instances and Auto Scaling groups. Increase the service quota so that sufficient concurrent functions can run at the same time.
정답 3번
Correct
Correct. The Auto Scaling group can scale in response to changes in system load in an SQS queue. Even if the Auto Scaling group is at its maximum capacity, jobs will be saved in the queue and they will be processed when compute resources become available. To learn more, see: Scaling based on Amazon SQS
17.
Question 17
A company is developing an application that runs on Amazon EC2 instances in a private subnet. The EC2 instances use a NAT gateway to access the internet. A solutions architect must provide a secure option so that developers can log in to the instances. Which solution meets these requirements MOST cost-effectively?
4.3 Design cost-optimized network architectures
0 / 1 point
Configure AWS Systems Manager Session Manager for the EC2 instances to enable login. è 이게 답인가?
Configure a bastion host in a public subnet to log in to the EC2 instances in a private subnet.
Use the existing NAT gateway to log in to the EC2 instances in a private subnet. è 두번째 시도 답
A NAT gateway is a Network Address Translation (NAT) service. You can use a NAT gateway so that instances in a private subnet can connect to services outside your VPC but external services cannot initiate a connection with those instances.
Configure AWS Site-to-Site VPN to log in directly to the EC2 instances.
Incorrect
Incorrect. Bastion hosts solve the functional requirement, but they increase costs because one or more instances would be required. To learn more, see: AWS Quick Starts - Linux Bastion Hosts on AWS
Incorrect
Incorrect. You cannot use NAT gateways to log in to EC2 instances because NAT gateways are gateways that handle only outbound traffic. To learn more, see: NAT gateways
두번째 시도에 3번 – 틀림
정답 1번
Correct
Correct. Session Manager provides secure and auditable instance management without the need to open inbound ports, maintain bastion hosts, or manage SSH keys. There is no additional charge for accessing EC2 instances by using Session Manager. To learn more about Session Manager, see: AWS Systems Manager Session Manager To learn more about Session Manager pricing, see: AWS Systems Manager pricing
18.
Question 18
A company is using an Amazon S3 bucket to store archived data for audits. The company needs long-term storage for the data. The data is rarely accessed and must be available for retrieval the next business day. After a quarterly review, the company wants to reduce the storage cost for the S3 bucket. A solutions architect must recommend the most cost-effective solution to store the archived data. Which solution will meet these requirements?
4.1 Identify cost-effective storage solutions
1 / 1 point
Store the data on an Amazon EC2 instance that uses Amazon Elastic Block Store (Amazon EBS).
Use an S3 Lifecycle configuration rule to move the data to S3 Standard-Infrequent Access (S3 Standard-IA).
Store the data in S3 Glacier.
Store the data in another S3 bucket in a different AWS Region.
정답 3번
Correct
Correct. Out of these options, S3 Glacier is the most cost-effective solution. S3 Glacier is a good fit for archival data that does not need to be frequently accessed or modified. For more information about S3 Glacier, see: What Is S3 Glacier? To learn more about retrieval options for S3 Glacier, see: Retrieving S3 Glacier Archives
19.
Question 19
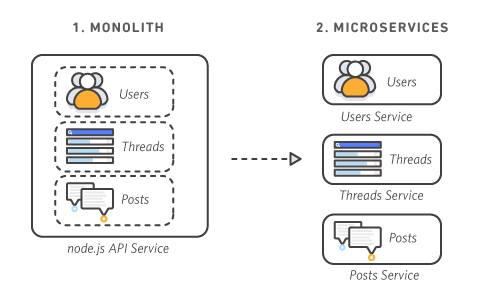
A solutions architect must create a disaster recovery (DR) solution for a company's business-critical applications. The DR site must reside in a different AWS Region than the primary site. The solution requires a recovery point objective (RPO) in seconds and a recovery time objective (RTO) in minutes. The solution also requires the deployment of a completely functional, but scaled-down version of the applications. Which DR strategy will meet these requirements?
1.2 Design highly available and/or fault-tolerant architectures
0 / 1 point
Multi-site active-active
Backup and restore
Pilot light
Warm standby è 이게 답인 것 같음
Incorrect
Incorrect. Multi-site active-active has an RPO and an RTO in real time and is considered a hot standby. Though this strategy will meet the RPO and RTO requirements, it is not a scaled down version of the applications (a stated requirement), and it will be more expensive than other options. To learn more about various DR strategies, see: Plan for Disaster Recovery (DR) - Use defined recovery strategies to meet the recovery objectives
정답 4번 – 두번째 시도에 맞춤
Correct
Correct. With warm standby (fully working at low capacity), all components run at a low capacity. The RPO is in seconds, and the RTO is in minutes. To learn more about various DR strategies, see: Plan for Disaster Recovery (DR) - Use defined recovery strategies to meet the recovery objectives
20.
Question 20
A financial services company is migrating its multi-tier web application to AWS. The application architecture consists of a fleet of web servers, application servers, and an Oracle database. The company must have full control over the database's underlying operating system, and the database must be highly available. Which approach should a solutions architect use for the database tier to meet these requirements?
1.2 Design highly available and/or fault-tolerant architectures
1 / 1 point
Migrate the database to an Amazon RDS for Oracle DB Single-AZ DB instance.
Migrate the database to an Amazon RDS for Oracle Multi-AZ DB instance.
Migrate to Amazon EC2 instances in two Availability Zones. Install Oracle Database and configure the instances to operate as a cluster.
Migrate to Amazon EC2 instances in a single Availability Zone. Install Oracle Database and configure the instances to operate as a cluster.
정답 3번
Correct
Correct. This solution provides the company with full control of the database operating system. The solution also provides high availability. To learn more about when Amazon EC2 is a good option, see: Amazon EC2 for Oracle
21.
Question 21
A hospital client is migrating from another cloud provider to AWS and is looking for advice on modernizing as they migrate. They have containerized applications that run on tablets. During spikes caused by increases in patient visits, the communications from the applications to the central database occasionally fail. As a result, the client currently has the applications try to write to the central database once, and if that write fails, it writes to a dedicated application PostgreSQL database run by the hospital IT team on premises. Each of those PostgreSQL databases then sends batch information on to the central database. The client is asking for recommendations for migrating or refactoring the database write process to decrease operational overhead. What should the solutions architect recommend? (Select TWO.)
4.2 Identify cost-effective compute and database services
1 / 1 point
Migrate the containerized applications to AWS Fargate.
Migrate the local databases to Aurora Serverless for PostgreSQL.
Correct
Correct. PostgreSQL has been turned into a kind of messaging service (holding all of the data until the batch job runs), and that is better handled by a queuing service. However, moving to Aurora Serverless will still decrease overhead for running the database, and it is a valid answer. To learn more, see: Amazon Aurora Serverless
Migrate the PostgreSQL databases to an RDS instance with a read replica that replaces each of the local databases.
Refactor the applications to use Amazon Simple Queue Service and eliminate the local PostgreSQL databases.
Correct
Correct. The client can decouple the messaging aspect of the application and remove the databases (which are effectively a workaround messaging service). To learn more about, see: How Amazon SQS works
Refactor the central database to add an Amazon ElastiCache lazy loading cache in front of the database.
정답 2,4 번
22.
Question 22
A large international company has a management account in AWS Organizations, and over 50 individual accounts for each country they operate in. Each of the country accounts has least four VPCs set up for functional divisions. There is a high amount of trust across the accounts, and communication among all of the VPCs should be allowed. Each of the individual VPCs throughout the entire global organization will need to access an account and VPC that provide shared services to all the other accounts. How can the member accounts access the shared services VPC with the LEAST operational overhead?
2.3 Select high-performing networking solutions for a workload
1 / 1 point
Create an Application Load Balancer, with a target of the private IP address of the shared services VPC. Add a Certification Authority Authorization (CAA) record for the Application Load Balancer to Amazon Route 53. Point all requests for shared services in the routing tables of the VPCs to the CAA record.
Create a peering connection between each of the VPCs and the shared services VPC.
Create a Network Load Balancer across the Availability Zones in the shared services VPC. Create service consumer roles in IAM, and set endpoint connection acceptance to automatically accept. Create consumer endpoints in each division VPC and point to the Network Load Balancer.
Create a VPN connection between each of the VPCs and the shared service VPC.
정답 3번
Correct
Correct. This solution provides the general flow of how an AWS PrivateLink connection is established. To learn more, see: Interface VPC endpoints (AWS PrivateLink)
23.
Question 23
A SysOps administrator is looking into a way to automate the deployment of new SSL/TLS certificates to their web servers, and a centralized way to track and manage the deployed certificates. Which AWS service can the administrator use to fulfill the above-mentioned needs?
3.2 Design secure application tiers
1 / 1 point
AWS Key Management Service
AWS Certificate Manager
Configure AWS Systems Manager Run Command
AWS Systems Manager Parameter Store
정답 2번
Correct
Correct. AWS Certificate Manager (ACM) is a service that you can use to provision, manage, and deploy public and private Secure Sockets Layer/Transport Layer Security (SSL/TLS) certificates for use with AWS services and your internal, connected resources. SSL/TLS certificates are used to secure network communications and establish the identity of websites over the internet, in addition to resources on private networks. ACM reduces the time-consuming manual process of purchasing, uploading, and renewing SSL/TLS certificates. To learn more, see: AWS Certificate Manager
24.
Question 24
A client has created a website (www.example.com), with an Application Load Balancer in a public subnet. The load balancer targets an application hosted on EC2 instances in private subnets, which rely on an Amazon Aurora PostgreSQL-Compatible Edition DB instance in separate private subnets. When testing the website, static content from the EC2 instance is displayed, but any content driven by database queries fails to load. What should the administrator check?
1.1 Design a multi-tier architecture solution
0 / 1 point
Check the Amazon Route 53 CNAME record to ensure that www.example.com points to the top-level domain (example.com).
Check the network access control list (network ACL) of the application subnets for an outbound allow statement.
è 두번째 시도 답 틀림
Check that the route table for the database subnets includes a default route to the internet gateway for the VPC.
è 첫번째 시도 답 틀림
Check if the security group of the database subnet allows inbound traffic from the EC2 subnets. è 이게 답인가?
Incorrect
Incorrect. The database should be interacting with the EC2 subnet, which should return information to the Application Load Balancer. Providing access to the internet gateway could make the database subnet public instead of private. To learn more, see: Internet gateways
Incorrect
Incorrect. The EC2 instances are able to return information to the Application Load Balancer and out to the browser, so the network ACL is not blocking anything at the VPC level. To learn more, see: Security Groups and Network Access Control Lists (Network ACLs) (BP5)
두번째 시도 2번 – 틀림
정답 4번
Correct. The database security group is likely not configured for inbound traffic from the EC2 layer. To learn more, see: Security Groups and Network Access Control Lists (Network ACLs) (BP5)
25.
Question 25
A solutions architect has been tasked with designing a three-tier application for deployment in AWS. There will be a web tier as the frontend, a backend application tier for data processing, and a database that will be hosted on Amazon RDS. The application frontend will be distributed to end users by CloudFront. Following best practices, it is decided that there should not be any point-to-point dependencies between the different layers of the infrastructure. How many Elastic Load Balancing load balancers should the architect deploy in the architecture so that this application's design follows best practices?
1.1 Design a multi-tier architecture solution
0 / 1 point
Zero. Use the load balancer that is automatically enabled when CloudFront is deployed.
One load balancer. This load balancer would be between the web tier and the application tier.
Two load balancers. One public load balancer would direct traffic to the web tier, and one private load balancer would direct traffic to the application tier. è 이게 답인가?
Three load balancers. One public load balancer would direct traffic to the web tier. One private load balancer would direct traffic to the application tier. Another private load balancer would direct traffic to the Amazon RDS database.
Incorrect
Incorrect. Though deploying one load balancer is better than deploying none, the application might experience reliability issues between the tiers that do not have a load balancer in place. To learn more about best practices for deploying a web hosting environment, see: An AWS Cloud architecture for web hosting
정답 3번 – 두번째 시도에 맞춤
Correct
Correct.One load balancer will be deployed between CloudFront and the web tier. Another load balancer would be deployed between the web tier and the application tier. To learn more about best practices for deploying a web hosting environment, see: An AWS Cloud architecture for web hosting
26.
Question 26
The CIO of a company is concerned about the security of the account root user of their AWS account. How can the CIO ensure that the AWS account follows the best practices for logging in securely? (Select TWO.)
3.1 Design secure access to AWS resources
1 / 1 point
Enforce the use of an access key ID and secret access key for the account root user logins.
Enforce the use of MFA for the account root user logins.
Correct
Correct. For increased security, we recommend that you configure multi-factor authentication (MFA) to help protect your AWS resources. You can enable MFA for IAM users or the AWS account root user. When you enable MFA for the root user, it affects only the root user credentials. IAM users in the account are distinct identities with their own credentials, and each identity has its own MFA configuration. To learn more about using MFA for accounts in AWS Organizations, see: Best practices for member accounts To learn more about enabling MFA for the account root user, see: Using multi-factor authentication (MFA) in AWS
Enforce the account root user to assume a role to access the root user's own resources.
Enforce the use of complex passwords for member account root user logins.
Correct
Correct. The security of your account root user depends on the strength of its password. We recommend that you use a password that is long, complex, and not used anywhere else. To learn more about using complex passwords for accounts in AWS Organizations, see: Best practices for member accounts
Enforce the deletion of the AWS account so that it cannot be used.
정답 2,4번
27.
Question 27
A Solutions Architect has been tasked with creating a data store location that will be able to handle different file formats of unknown sizes. It is required that this data be highly available and protected from being accidentally deleted. What solution meets the requirements and is the MOST cost-effective?
3.3 Select appropriate data security options
1 / 1 point
Deploy an Amazon S3 bucket and enable Cross-Region Replication.
Deploy an Amazon DynamoDB table and enable Global Tables.
Deploy an Amazon S3 bucket and enable Object Versioning.
Deploy a database using Amazon RDS and configure a Multi-AZ deployment for that database.
정답 3번
Correct
Correct. Versioning-enabled buckets can help you recover objects from accidental deletion or overwrite. For example, if you delete an object, Amazon S3 inserts a delete marker instead of removing the object permanently. The delete marker becomes the current object version. If you overwrite an object, it results in a new object version in the bucket. A user can always restore the previous version. To learn more about object versioning, see: Using versioning in S3 buckets
28.
Question 28
An organization is planning to migrate from an on-premises data center to an AWS environment that spans multiple Availability Zones. A migration engineer has been tasked to plan how to transfer the home directories and other shared network attached storage from the data center to AWS. The migration design should support connections from multiple Amazon EC2 instances running the Linux operating system to this common shared storage platform. What storage option best fits their design?
1.4 Choose appropriate resilient storage
1 / 1 point
Transfer the files to Amazon S3 and access that data from the EC2 instances.
Transfer the files to the EC2 Instance Store attached to the EC2 instances.
Transfer the files to Amazon EFS and mount that file system to the EC2 instances.
Transfer the files to one EBS volume and mount that volume to the EC2 instances.
정답 3번
Correct
Correct. Amazon EFS is well suited to support a broad spectrum of use cases from home directories to business-critical applications. Amazon EFS is designed to provide massively parallel shared access to thousands of EC2 instances. To learn more, see: Amazon Elastic File System
29.
Question 29
A company is designing a human genome application using multiple Amazon EC2 Linux instances. The high performance computing (HPC) application requires low latency and high performance network communication between the instances. Which solution provides the LOWEST latency between the instances?
1.1 Design a multi-tier architecture solution
0 / 1 point
Launch the EC2 instances in a cluster placement group. è 이게 답인가?
Launch the EC2 instances in a spread placement group.
Launch the EC2 instances in an Auto Scaling group spanning multiple Regions.
Launch the EC2 instances in an Auto Scaling group spanning multiple Availability Zones within a Region.
Incorrect
Incorrect. Because a HPC platform would require packing instances close together, instances that span Availability Zones would not provide the lowest network latency. To learn more, see: What is Amazon EC2 Auto Scaling?
정답 1번 – 두번째 시도에 맞춤
Correct
Correct. In an EC2 cluster placement group, instances are physically close together inside an Availability Zone. With this strategy, workloads can achieve the low-latency network performance that is needed for tightly coupled, node-to-node communication that is typical of HPC applications. To learn more, see: Placement groups
30.
Question 30
A company has a web application in which customers can log in and read near-real-time status updates about their orders. The company hosts the application on Amazon EC2 instances and is expanding the application from the eu-west-1 Region into the us-east-1 Region. The application relies on an Amazon RDS for MySQL database. The company already has provisioned the necessary EC2 instances in the new Region. The company needs to deploy the application in us-east-1 with the least possible change to the application. The company also needs fast, local database queries in both Regions. Which modification of the database will meet these requirements?
2.4 Choose high-performing database solutions for a workload.
1 / 1 point
Migrate the RDS database to an Amazon Aurora global database. Add a secondary cluster in us-east-1.
Migrate the RDS database to an Amazon Aurora Serverless database. Configure automatic scaling in us-east-1.
Migrate the RDS database to an Amazon DynamoDB table. Create global tables for us-east-1.
Place an accelerator from AWS Global Accelerator in front of the RDS database to reduce the network latency from us-east-1.
정답 1번
Correct
Correct. This solution meets the requirements, and is designed for a replica latency of approximately 1 second. By using the global database, users receive a low-read latency, with writes occurring on the primary database cluster in eu-west-1. The current application can continue to use existing code that points to the local Aurora instance. To learn more, see: Using Amazon Aurora global databases
31.
Question 31
A company is building a distributed application, which will send sensor IoT data-- including weather conditions and wind speed from wind turbines--to the AWS Cloud for further processing. Because the nature of the data is spiky, the application needs to be able to scale. It is important to store the streaming data in a key-value database and then send it over to a centralized data lake, where it can be transformed, analyzed, and combined with diverse organizational datasets to derive meaningful insights and make predictions. Which combination of solutions would accomplish the business need with minimal operational overhead? (Select TWO.)
2.4 Choose high-performing database solutions for a workload.
0 / 1 point
Configure Amazon Kinesis to deliver streaming data to an Amazon S3 data lake. è 이게 답인가?
Correct
Correct. Kinesis can send streaming data to an Amazon S3 data lake. To learn more, see: Build a data lake using Amazon Kinesis Data Streams for Amazon DynamoDB and Apache Hudi
Use Amazon DocumentDB to store IoT sensor data.
Write AWS Lambda functions to deliver streaming data to Amazon S3.
Use Amazon DynamoDB to store the IoT sensor data, and enable DynamoDB Streams.
Correct
Correct. DynamoDB Streams can be used to start Lambda functions. Lambda could then be used to send an Amazon SNS notification, or take corrective measures if the threshold is breached. To learn more about DynamoDB Streams, see: Change Data Capture for DynamoDB Streams To learn more about use cases for DynamoDB Streams, see: DynamoDB Streams Use Cases and Design Patterns
Use Amazon Kinesis to deliver streaming data to Amazon Redshift, and enable Amazon Redshift Spectrum.
This should not be selected
Incorrect. Amazon Kinesis Data Firehose can deliver streaming data to Amazon Redshift. However, S3 is better choice for a data lake where data can be transformed, analyzed, and combined with diverse organizational datasets to derive meaningful insights and make predictions.
정답 1,4번 – 두번째 시도에 맞춤
'IoT > AWS Certificate' 카테고리의 다른 글
| Udemy - Amazon Web Services (AWS) Certified - 4 Certifications! (0) | 2020.04.03 |
|---|---|
| AWS Practitioner Certificate - Free Braindumps (0) | 2020.02.18 |
| AWS Certified Cloud Practitioner - BackSpace Academy - Udemy course (0) | 2020.02.13 |
| AWS Cloud Practitioner Essentials (Digital) (Korean) - 03 (0) | 2020.01.05 |
| AWS Cloud Practitioner Essentials (Digital) (Korean) - 02 (0) | 2020.01.02 |
| AWS Cloud Practitioner Essentials (Digital) (Korean) - 01 (0) | 2019.12.29 |
| AWS Certified developer associate exam samples 2 (0) | 2018.02.15 |
| AWS Certified developer associate exam samples (2) | 2018.01.26 |
| [AWS Certificate] Developer - VPC memo (1) | 2017.11.29 |
| [AWS Certificate] Developer - Route53 memo (0) | 2017.11.25 |