D2L - 5. Multilayer Perceptrons

5. Multilayer Perceptrons — Dive into Deep Learning 1.0.0-beta0 documentation (d2l.ai)

5. Multilayer Perceptrons — Dive into Deep Learning 1.0.0-beta0 documentation

 

5. Multilayer Perceptrons

 

In this chapter, we will introduce your first truly deep network. The simplest deep networks are called multilayer perceptrons, and they consist of multiple layers of neurons each fully connected to those in the layer below (from which they receive input) and those above (which they, in turn, influence). Although automatic differentiation significantly simplifies the implementation of deep learning algorithms, we will dive deep into how these gradients are calculated in deep networks. Then we will be ready to discuss issues relating to numerical stability and parameter initialization that are key to successfully training deep networks. When we train such high-capacity models we run the risk of overfitting. Thus, we will revisit regularization and generalization for deep networks. Throughout, we aim to give you a firm grasp not just of the concepts but also of the practice of using deep networks. At the end of this chapter, we apply what we have introduced so far to a real case: house price prediction. We punt matters relating to the computational performance, scalability, and efficiency of our models to subsequent chapters.

 

이 장에서는 최초의 진정한 딥 네트워크를 소개합니다. 가장 단순한 딥 네트워크는 다층 퍼셉트론(multilayer perceptrons)이라고 하며, 이들은 각각 아래 계층(입력을 받는)과 위(그들이 영향을 주는) 계층에 완전히 연결된 여러 계층의 뉴런으로 구성됩니다. 자동 미분(automatic differentiation)은 딥 러닝 알고리즘의 구현을 상당히 단순화하지만 딥 네트워크에서 이러한 그래디언트(기울기)를 계산하는 방법에 대해 자세히 알아볼 것입니다. 그런 다음 딥 네트워크를 성공적으로 교육하는 데 중요한 수치적 안정성 및 매개변수 초기화와 관련된 문제를 논의할 준비가 될 것입니다. 이러한 고용량 모델을 교육할 때 과적합의 위험이 있습니다. 따라서 딥 네트워크에 대한 정규화 및 일반화를 다시 살펴보겠습니다. 전반적으로 개념뿐만 아니라 심층 네트워크 사용 실습에 대한 확고한 이해를 제공하는 것을 목표로 합니다. 이 장의 끝에서는 지금까지 소개한 내용을 실제 사례인 주택 가격 예측에 적용합니다. 모델의 계산 성능, 확장성 및 효율성과 관련된 문제는 다음 장에서 다루겠습니다.

 

 

 

https://youtu.be/XG73maPwDl8

 

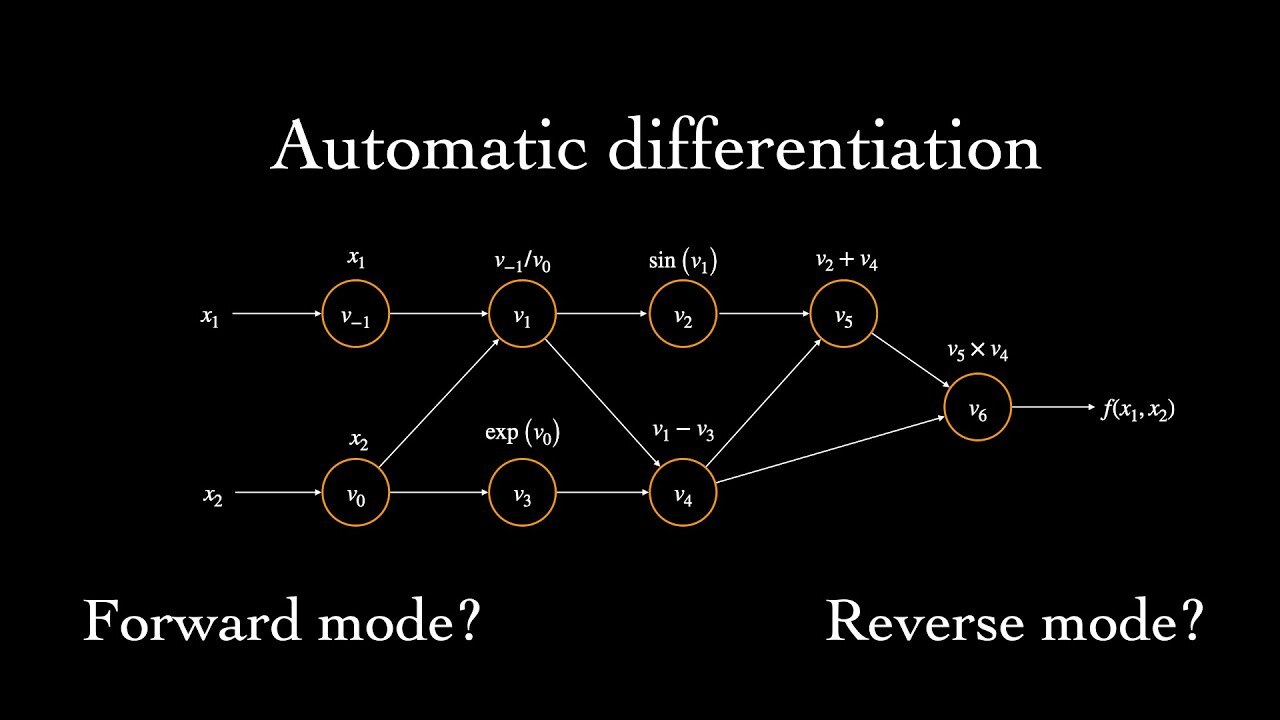
What does Automatic Differentiation (AutoDiff, AD) mean?

 

Automatic differentiation is a technique used in computational mathematics and computer science to automatically and efficiently compute the derivatives of mathematical functions. It enables the calculation of exact gradients of functions with respect to their input variables.

 

자동 미분(Automatic differentiation)은 수치 계산 및 컴퓨터 과학에서 사용되는 기술로, 수학 함수의 도함수(derivatives of mathematical functions)를 자동으로 효율적으로 계산하는 방법입니다. 이는 입력 변수에 대한 함수의 정확한 그레이디언트(기울기)를 계산하는 데 사용됩니다.

 

In traditional manual differentiation, the derivatives of functions are computed by hand using mathematical rules and formulas. This process can be tedious and error-prone, especially for complex functions. Automatic differentiation, on the other hand, automates the process by breaking down complex functions into a series of elementary operations, such as addition, subtraction, multiplication, and division.

 

전통적인 수동 미분에서는 함수의 도함수(derivatives)를 수학적인 규칙과 공식을 사용하여 수동으로 계산합니다. 이 과정은 복잡한 함수에 대해서는 지루하고 실수할 가능성이 높습니다. 그에 반해 자동 미분은 복잡한 함수를 덧셈, 뺄셈, 곱셈, 나눗셈 등의 기본 연산들로 분해하여 처리합니다.

 

During the forward pass of automatic differentiation, the values of the input variables are evaluated and stored. Then, during the backward pass, the derivatives of the output variables with respect to the input variables are computed by applying the chain rule of calculus to the elementary operations. This process allows for the efficient computation of gradients without the need for manual derivation.

 

자동 미분의 순방향 패스에서는 입력 변수의 값들이 계산되고 저장됩니다. 그리고 역방향 패스에서는 계산된 출력 변수에 대한 입력 변수의 도함수를 기본 연산들에 대해 미분 체인 규칙을 적용하여 계산합니다. 이 과정을 통해 도함수를 수동으로 계산하지 않고도 효율적으로 그레이디언트(기울기)를 계산할 수 있습니다.

 

Automatic differentiation is widely used in machine learning and deep learning algorithms, where gradients play a crucial role in optimizing models through techniques like gradient descent. It enables efficient gradient computation in complex models with a large number of parameters, making it a fundamental tool for training neural networks and solving optimization problems.

 

자동 미분은 머신 러닝과 딥 러닝 알고리즘에서 널리 사용되며, 그레이디언트(기울기)가 경사하강법과 같은 기법을 통해 모델을 최적화하는 데 중요한 역할을 합니다. 이를 통해 많은 파라미터를 가진 복잡한 모델에서도 효율적인 그레이디언트 계산이 가능하며, 신경망의 학습과 최적화 문제 해결에 핵심적인 도구로 사용됩니다

 

 

Multilayer Perceptron

 

https://youtu.be/2ZFUlEFAbBk

 

https://youtu.be/z2NN1QQabQs

 

https://youtu.be/s1QIaDV-oOI

 

 

Multilayer Perceptron 이란?

 

Multilayer Perceptrons (MLPs) are a type of artificial neural network that consists of multiple layers of perceptron units. Perceptrons, also known as artificial neurons, are the fundamental building blocks of neural networks. MLPs are called "multilayer" because they have an input layer, one or more hidden layers, and an output layer.

 

다중 계층 퍼셉트론(Multilayer Perceptrons, MLP)은 여러 개의 퍼셉트론 유닛으로 구성된 인공 신경망의 한 종류입니다. 퍼셉트론은 인공 신경망의 기본 구성 요소로서, MLP는 입력층, 하나 이상의 은닉층, 그리고 출력층으로 구성된 "다중 계층"을 가지고 있어서 이렇게 불립니다.

 

Each perceptron in an MLP receives inputs, applies a linear transformation to the inputs using weights, and passes the transformed values through an activation function to produce an output. The output of one layer serves as the input to the next layer, and this process continues until the final output layer is reached.

 

MLP의 각 퍼셉트론은 입력을 받고, 가중치를 사용하여 입력에 선형 변환을 적용한 후, 활성화 함수를 통해 출력을 생성합니다. 한 계층의 출력은 다음 계층의 입력으로 사용되며, 이 과정은 최종 출력층에 도달할 때까지 계속됩니다.

 

The hidden layers in MLPs allow for the learning of complex, nonlinear relationships between inputs and outputs. The weights and biases of the perceptrons in each layer are adjusted during the training process using optimization algorithms like gradient descent, allowing the network to learn the optimal parameters for making accurate predictions or classifications.

 

MLP의 은닉층은 입력과 출력 간의 복잡하고 비선형적인 관계를 학습할 수 있도록 합니다. 각 계층의 퍼셉트론의 가중치와 편향은 경사 하강법과 같은 최적화 알고리즘을 사용하여 학습 과정에서 조정되어, 네트워크가 정확한 예측이나 분류를 위한 최적의 매개변수를 학습할 수 있습니다.

 

MLPs have been widely used in various machine learning tasks, including image recognition, natural language processing, and regression problems. Their ability to model complex relationships makes them effective in capturing intricate patterns in data.

 

MLP는 이미지 인식, 자연어 처리, 회귀 문제 등 다양한 기계 학습 작업에서 널리 사용되고 있습니다. 복잡한 관계를 모델링할 수 있는 능력을 가지고 있어서 데이터의 복잡한 패턴을 잘 포착할 수 있습니다.

 

• 5.1. Multilayer Perceptrons
  • 5.1.1. Hidden Layers
  • 5.1.2. Activation Functions
  • 5.1.3. Summary and Discussion
  • 5.1.4. Exercises
• 5.2. Implementation of Multilayer Perceptrons
  • 5.2.1. Implementation from Scratch
  • 5.2.2. Concise Implementation
  • 5.2.3. Summary
  • 5.2.4. Exercises
• 5.3. Forward Propagation, Backward Propagation, and Computational Graphs
  • 5.3.1. Forward Propagation
  • 5.3.2. Computational Graph of Forward Propagation
  • 5.3.3. Backpropagation
  • 5.3.4. Training Neural Networks
  • 5.3.5. Summary
  • 5.3.6. Exercises
• 5.4. Numerical Stability and Initialization
  • 5.4.1. Vanishing and Exploding Gradients
  • 5.4.2. Parameter Initialization
  • 5.4.3. Summary
  • 5.4.4. Exercises
• 5.5. Generalization in Deep Learning
  • 5.5.1. Revisiting Overfitting and Regularization
  • 5.5.2. Inspiration from Nonparametrics
  • 5.5.3. Early Stopping
  • 5.5.4. Classical Regularization Methods for Deep Networks
  • 5.5.5. Summary
  • 5.5.6. Exercises
• 5.6. Dropout
  • 5.6.1. Dropout in Practice
  • 5.6.2. Implementation from Scratch
  • 5.6.3. Concise Implementation
  • 5.6.4. Summary
  • 5.6.5. Exercises
• 5.7. Predicting House Prices on Kaggle
  • 5.7.1. Downloading Data
  • 5.7.2. Kaggle
  • 5.7.3. Accessing and Reading the Dataset
  • 5.7.4. Data Preprocessing
  • 5.7.5. Error Measure
  • 5.7.6. \(K\)-Fold Cross-Validation
  • 5.7.7. Model Selection
  • 5.7.8. Submitting Predictions on Kaggle
  • 5.7.9. Summary
  • 5.7.10. Exercises

 

.