5.4. Numerical Stability and Initialization — Dive into Deep Learning 1.0.0-beta0 documentation
d2l.ai
5.4. Numerical Stability and Initialization
Thus far, every model that we have implemented required that we initialize its parameters according to some pre-specified distribution. Until now, we took the initialization scheme for granted, glossing over the details of how these choices are made. You might have even gotten the impression that these choices are not especially important. To the contrary, the choice of initialization scheme plays a significant role in neural network learning, and it can be crucial for maintaining numerical stability.
지금까지 우리가 구현한 모든 모델은 미리 지정된 분포에 따라 매개변수를 초기화해야 했습니다. 지금까지 우리는 초기화 체계를 당연하게 여겼고 이러한 선택이 어떻게 이루어지는지에 대한 세부 사항을 얼버무렸습니다. 이러한 선택이 특별히 중요하지 않다는 인상을 받았을 수도 있습니다. 반대로 초기화 방식의 선택은 신경망 학습에서 중요한 역할을 하며 수치적 안정성을 유지하는 데 중요할 수 있습니다.
Moreover, these choices can be tied up in interesting ways with the choice of the nonlinear activation function. Which function we choose and how we initialize parameters can determine how quickly our optimization algorithm converges. Poor choices here can cause us to encounter exploding or vanishing gradients while training. In this section, we delve into these topics with greater detail and discuss some useful heuristics that you will find useful throughout your career in deep learning.
또한 이러한 선택은 비선형 활성화 함수의 선택과 함께 흥미로운 방식으로 연결될 수 있습니다. 어떤 함수를 선택하고 매개변수를 초기화하는 방법에 따라 최적화 알고리즘이 수렴하는 속도가 결정됩니다. 잘못된 선택으로 인해 훈련하는 동안 그라디언트가 폭발하거나 사라지는 문제가 발생할 수 있습니다. 이 섹션에서는 이러한 주제를 더 자세히 살펴보고 딥 러닝 경력 전반에 걸쳐 유용한 휴리스틱에 대해 논의합니다.
heuristics 란?
Heuristics refers to problem-solving or decision-making strategies that are based on practical experience and common sense, rather than relying on exhaustive analysis or optimization algorithms. Heuristics are often used in situations where finding an optimal solution is computationally expensive or time-consuming.
휴리스틱(heuristics)은 철학적으로 최적화 알고리즘의 철저한 분석이나 최적해를 찾는 데에 의존하지 않고, 실용적인 경험과 상식을 기반으로 하는 문제 해결이나 의사 결정 전략을 의미합니다. 휴리스틱은 최적해를 찾는 것이 계산적으로 매우 비용이 들거나 시간이 오래 걸리는 상황에서 주로 사용됩니다.
Heuristics can be thought of as "rules of thumb" or practical guidelines that help guide decision-making in complex or uncertain situations. They are often derived from past experience, intuition, or expert knowledge in a particular domain. Heuristics provide shortcuts or approximations that allow individuals or systems to make reasonably good decisions quickly and efficiently, even in the absence of complete information.
휴리스틱은 "두뇌의 지식이론"이라고 생각할 수 있으며, 복잡하거나 불확실한 상황에서 의사 결정을 돕는 실용적인 지침이나 규칙을 말합니다. 이러한 휴리스틱은 과거의 경험, 직관 또는 특정 분야의 전문 지식에서 유도될 수 있습니다. 휴리스틱은 완전한 정보가 없는 상황에서도 개인이나 시스템이 상당히 좋은 결정을 빠르고 효율적으로 내릴 수 있도록 해주는 근사치나 단축된 방법을 제공합니다.
Heuristics are commonly employed in various fields, including problem-solving, decision-making, optimization, artificial intelligence, and cognitive psychology. They serve as practical problem-solving techniques that balance efficiency and accuracy by trading off optimality for speed and simplicity.
휴리스틱은 문제 해결, 의사 결정, 최적화, 인공지능, 인지 심리학 등 다양한 분야에서 흔히 사용됩니다. 이들은 속도와 간단함을 위해 최적성을 희생함으로써 효율성과 정확성을 균형있게 조절하는 실용적인 문제 해결 기술로서 사용됩니다.
%matplotlib inline
import torch
from d2l import torch as d2l위 코드는 주피터 노트북(Jupyter Notebook)에서 그래프를 인라인으로 표시하기 위한 매직 커맨드입니다. 이 매직 커맨드는 주피터 노트북 환경에서 그래프를 생성한 셀 아래에 결과를 바로 출력하는 역할을 합니다.
또한, torch 모듈과 d2l 라이브러리의 torch 모듈을 가져옵니다. torch는 파이토치(PyTorch)의 기본 라이브러리이며, d2l의 torch 모듈은 "Dive into Deep Learning" 책의 예제와 유틸리티 함수를 포함하고 있습니다. 이러한 모듈들을 임포트하여 파이토치와 관련된 작업을 수행할 수 있습니다.
따라서, 이 코드는 주피터 노트북 환경에서 그래프를 인라인으로 표시하기 위한 설정을 하고, 파이토치와 관련된 모듈을 가져오는 역할을 합니다.
5.4.1. Vanishing and Exploding Gradients
Consider a deep network with L layers, input x and output o. With each layer l defined by a transformation f1 parameterized by weights W(l), whose hidden layer output is ℎ(l) (let ℎ(0)=x), our network can be expressed as:
L 레이어, 입력 x 및 출력 o가 있는 심층 네트워크를 고려하십시오. 가중치 W(l)에 의해 매개변수화된 변환 f1에 의해 정의된 각 레이어 l은 숨겨진 레이어 출력이 ℎ(l)(let ℎ(0)=x)인 네트워크를 다음과 같이 표현할 수 있습니다.
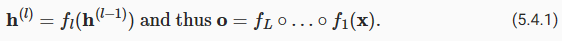
If all the hidden layer output and the input are vectors, we can write the gradient of o with respect to any set of parameters W(l) as follows:
숨겨진 레이어의 모든 출력과 입력이 벡터인 경우 다음과 같이 매개변수 세트 W(l)에 대한 o의 그래디언트를 작성할 수 있습니다.
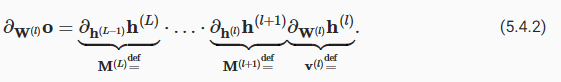
In other words, this gradient is the product of L−l matrices M(l)⋅…⋅M(l+1) and the gradient vector v(l). Thus we are susceptible to the same problems of numerical underflow that often crop up when multiplying together too many probabilities. When dealing with probabilities, a common trick is to switch into log-space, i.e., shifting pressure from the mantissa to the exponent of the numerical representation. Unfortunately, our problem above is more serious: initially the matrices M(l) may have a wide variety of eigenvalues. They might be small or large, and their product might be very large or very small.
즉, 이 그래디언트는 L-l 행렬 M(l)⋅…⋅M(l+1)과 그래디언트 벡터 v(l)의 곱입니다. 따라서 우리는 너무 많은 확률을 함께 곱할 때 종종 발생하는 동일한 수치적 언더플로 문제에 취약합니다. 확률을 다룰 때 일반적인 트릭은 로그 공간으로 전환하는 것입니다. 즉, 가수에서 숫자 표현의 지수로 압력을 이동하는 것입니다. 불행히도 위의 문제는 더 심각합니다. 처음에는 행렬 M(l)이 다양한 고유값을 가질 수 있습니다. 그들은 작거나 클 수 있으며 그들의 제품은 매우 크거나 매우 작을 수 있습니다.
The risks posed by unstable gradients go beyond numerical representation. Gradients of unpredictable magnitude also threaten the stability of our optimization algorithms. We may be facing parameter updates that are either (i) excessively large, destroying our model (the exploding gradient problem); or (ii) excessively small (the vanishing gradient problem), rendering learning impossible as parameters hardly move on each update.
불안정한 기울기로 인한 위험은 수치 표현을 넘어선다. 예측할 수 없는 크기의 경사도 최적화 알고리즘의 안정성을 위협합니다. 우리는 (i) 과도하게 커서 모델을 파괴하는(폭발하는 그래디언트 문제) 매개변수 업데이트에 직면할 수 있습니다. 또는 (ii) 지나치게 작아서(기울기 소실 문제) 각 업데이트에서 매개변수가 거의 움직이지 않아 학습이 불가능해집니다.
5.4.1.1. Vanishing Gradients
One frequent culprit causing the vanishing gradient problem is the choice of the activation function σ that is appended following each layer’s linear operations. Historically, the sigmoid function 1/(1+exp(−x)) (introduced in Section 5.1) was popular because it resembles a thresholding function. Since early artificial neural networks were inspired by biological neural networks, the idea of neurons that fire either fully or not at all (like biological neurons) seemed appealing. Let’s take a closer look at the sigmoid to see why it can cause vanishing gradients.
Vanishing Gradient 문제를 일으키는 흔한 원인 중 하나는 각 레이어의 선형 연산 다음에 추가되는 활성화 함수 σ (sigma)의 선택입니다. 역사적으로 시그모이드 함수 1/(1+exp(−x))(섹션 5.1에서 소개됨)는 임계값 함수와 유사하기 때문에 널리 사용되었습니다. 초기 인공 신경망은 생물학적 신경망에서 영감을 받았기 때문에 (생물학적 뉴런과 같이) 완전히 또는 전혀 발화하지 않는 뉴런에 대한 아이디어가 매력적으로 보였습니다. 시그모이드를 자세히 살펴보고 기울기가 사라지는 이유를 살펴보겠습니다.
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.sigmoid(x)
y.backward(torch.ones_like(x))
d2l.plot(x.detach().numpy(), [y.detach().numpy(), x.grad.numpy()],
legend=['sigmoid', 'gradient'], figsize=(4.5, 2.5))
위 코드는 시그모이드 함수(sigmoid)를 사용하여 입력 x에 대한 출력 y와 그래디언트를 계산하고, 그 결과를 그래프로 나타내는 역할을 합니다.
먼저, torch.arange 함수를 사용하여 -8.0부터 8.0까지 0.1 간격으로 등간격의 텐서 x를 생성합니다. requires_grad=True 옵션을 사용하여 이 텐서가 연산 그래프에서 역전파를 통해 그래디언트를 계산할 수 있도록 설정합니다.
다음으로, torch.sigmoid 함수를 사용하여 입력 x에 대한 시그모이드 값을 계산하여 출력 y를 얻습니다. 시그모이드 함수는 0과 1 사이의 값을 출력하는 활성화 함수입니다.
그리고 나서 y.backward(torch.ones_like(x))를 호출하여 y를 기준으로 역전파를 수행하여 그래디언트를 계산합니다. 이때, torch.ones_like(x)는 x와 같은 모양(shape)의 1로 채워진 텐서를 생성하여 역전파에 사용됩니다.
마지막으로, d2l.plot 함수를 사용하여 그래프를 그립니다. x.detach().numpy()를 통해 x 텐서를 넘파이 배열로 변환하여 x축으로 사용하고, [y.detach().numpy(), x.grad.numpy()]를 통해 y와 그래디언트 값을 리스트로 전달합니다. legend 인자를 통해 그래프의 범례를 지정하고, figsize를 통해 그래프의 크기를 설정합니다.
이 코드는 입력 x에 대한 시그모이드 함수의 출력과 그래디언트를 계산하고, 그 결과를 그래프로 나타내는 역할을 수행합니다.
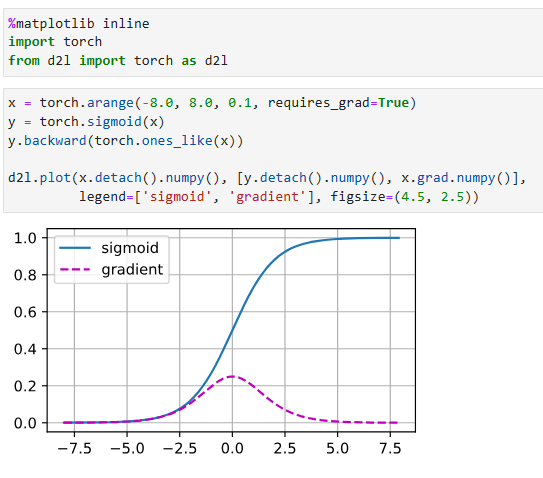
As you can see, the sigmoid’s gradient vanishes both when its inputs are large and when they are small. Moreover, when backpropagating through many layers, unless we are in the Goldilocks zone, where the inputs to many of the sigmoids are close to zero, the gradients of the overall product may vanish. When our network boasts many layers, unless we are careful, the gradient will likely be cut off at some layer. Indeed, this problem used to plague deep network training. Consequently, ReLUs, which are more stable (but less neurally plausible), have emerged as the default choice for practitioners.
보시다시피 시그모이드의 그래디언트는 입력이 클 때와 작을 때 모두 사라집니다. 또한 많은 계층을 통해 역전파할 때 많은 시그모이드에 대한 입력이 0에 가까운 Goldilocks 영역에 있지 않는 한 전체 제품의 그래디언트가 사라질 수 있습니다. 네트워크가 많은 레이어를 자랑할 때 주의하지 않으면 그라디언트가 일부 레이어에서 잘릴 수 있습니다. 실제로 이 문제는 심층 네트워크 훈련을 괴롭히는 데 사용되었습니다. 결과적으로 더 안정적인 (신경적으로 덜 타당함) ReLU가 실무자를 위한 기본 선택으로 부상했습니다.
5.4.1.2. Exploding Gradients
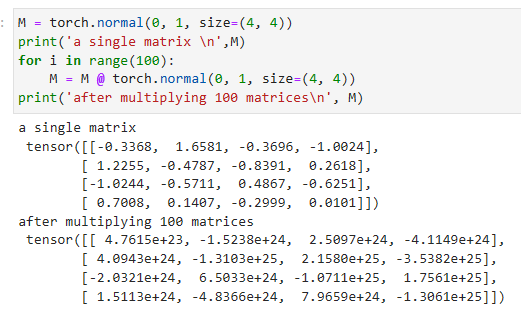
The opposite problem, when gradients explode, can be similarly vexing. To illustrate this a bit better, we draw 100 Gaussian random matrices and multiply them with some initial matrix. For the scale that we picked (the choice of the variance σ2=1), the matrix product explodes. When this happens due to the initialization of a deep network, we have no chance of getting a gradient descent optimizer to converge.
그래디언트가 폭발하는 반대의 문제도 비슷하게 성가실 수 있습니다. 이를 좀 더 잘 설명하기 위해 100개의 가우시안 랜덤 행렬을 그리고 초기 행렬과 곱합니다. 우리가 선택한 척도(분산 σ2=1 선택)에 대해 행렬 곱이 폭발합니다. 딥 네트워크의 초기화로 인해 이런 일이 발생하면 경사 하강 최적화 프로그램이 수렴할 기회가 없습니다.
M = torch.normal(0, 1, size=(4, 4))
print('a single matrix \n',M)
for i in range(100):
M = M @ torch.normal(0, 1, size=(4, 4))
print('after multiplying 100 matrices\n', M)
위 코드는 주어진 행렬 M을 반복하여 다른 행렬과 곱한 후 최종 결과를 출력하는 역할을 합니다.
먼저, torch.normal 함수를 사용하여 평균이 0이고 표준편차가 1인 정규 분포에서 크기가 (4, 4)인 행렬 M을 생성합니다. 이 행렬은 초기 값으로 사용됩니다.
그 다음, for 루프를 통해 100번의 반복을 수행합니다. 반복마다 M과 평균이 0이고 표준편차가 1인 정규 분포에서 크기가 (4, 4)인 다른 행렬을 곱하여 M을 갱신합니다. @ 연산자를 사용하여 행렬 곱셈을 수행합니다.
마지막으로, 반복이 끝난 후 M을 출력합니다. 이는 초기 행렬 M을 100번 반복하여 다른 행렬과 곱한 결과를 보여줍니다.
따라서, 위 코드는 초기 행렬을 반복적으로 다른 행렬과 곱한 후 최종 결과를 출력하는 역할을 합니다.
5.4.1.3. Breaking the Symmetry
Another problem in neural network design is the symmetry inherent in their parametrization. Assume that we have a simple MLP with one hidden layer and two units. In this case, we could permute the weights W(1) of the first layer and likewise permute the weights of the output layer to obtain the same function. There is nothing special differentiating the first hidden unit vs. the second hidden unit. In other words, we have permutation symmetry among the hidden units of each layer.
신경망 설계의 또 다른 문제는 매개변수화에 내재된 대칭성입니다. 하나의 숨겨진 레이어와 두 개의 유닛이 있는 간단한 MLP가 있다고 가정합니다. 이 경우 첫 번째 레이어의 가중치 W(1)을 치환하고 마찬가지로 출력 레이어의 가중치를 치환하여 동일한 함수를 얻을 수 있습니다. 첫 번째 숨겨진 유닛과 두 번째 숨겨진 유닛을 구별하는 특별한 것은 없습니다. 즉, 각 레이어의 숨겨진 단위 간에 순열 대칭이 있습니다.
This is more than just a theoretical nuisance. Consider the aforementioned one-hidden-layer MLP with two hidden units. For illustration, suppose that the output layer transforms the two hidden units into only one output unit. Imagine what would happen if we initialized all of the parameters of the hidden layer as W(1)=c for some constant c. In this case, during forward propagation either hidden unit takes the same inputs and parameters, producing the same activation, which is fed to the output unit. During backpropagation, differentiating the output unit with respect to parameters W(1) gives a gradient whose elements all take the same value. Thus, after gradient-based iteration (e.g., minibatch stochastic gradient descent), all the elements of W(1) still take the same value. Such iterations would never break the symmetry on its own and we might never be able to realize the network’s expressive power. The hidden layer would behave as if it had only a single unit. Note that while minibatch stochastic gradient descent would not break this symmetry, dropout regularization (to be introduced later) would!
이것은 이론적인 성가신 것 이상입니다. 두 개의 숨겨진 유닛이 있는 앞서 언급한 하나의 숨겨진 레이어 MLP를 고려하십시오. 설명을 위해 출력 레이어가 두 개의 숨겨진 유닛을 단 하나의 출력 유닛으로 변환한다고 가정합니다. 어떤 상수 c에 대해 은닉층의 모든 매개변수를 W(1)=c로 초기화하면 어떤 일이 일어날지 상상해 보십시오. 이 경우 순방향 전파 중에 히든 유닛은 동일한 입력과 매개변수를 사용하여 출력 유닛에 공급되는 동일한 활성화를 생성합니다. 역전파 중에 매개변수 W(1)에 대해 출력 단위를 미분하면 모든 요소가 동일한 값을 갖는 기울기가 제공됩니다. 따라서 그래디언트 기반 반복(gradient-based iteration)(예: 미니배치 확률적 그래디언트 디센트) 후에도 W(1)의 모든 요소는 여전히 동일한 값을 갖습니다. 그러한 반복은 그 자체로는 결코 대칭을 깨뜨리지 않을 것이며 우리는 결코 네트워크의 표현력을 깨닫지 못할 수도 있습니다. 숨겨진 계층은 단일 단위만 있는 것처럼 동작합니다. 미니배치 확률적 경사하강법(minibatch stochastic gradient descent)은 이 대칭성을 깨뜨리지 않지만 드롭아웃 정규화(-dropout regularization-, 나중에 소개됨)는 깨뜨릴 것입니다!
dropout regularization 이란?
Dropout regularization is a technique used in neural networks to prevent overfitting. It involves randomly "dropping out" (setting to zero) a certain proportion of the neurons in a layer during the training phase. By doing so, dropout regularization encourages the network to learn more robust and generalizable features by preventing individual neurons from relying too much on specific input patterns or co-adapting with other neurons. During inference or testing, all neurons are used, but their outputs are scaled by the dropout probability used during training to ensure consistent behavior.
드롭아웃 정규화(Dropout regularization)는 신경망에서 과적합을 방지하기 위해 사용되는 기법입니다. 이 기법은 훈련 단계에서 레이어의 일부 뉴런을 무작위로 "드롭아웃"시켜(값을 0으로 설정) 사용합니다. 이를 통해 드롭아웃 정규화는 개별 뉴런이 특정 입력 패턴에 지나치게 의존하거나 다른 뉴런과 공동으로 적응하는 것을 방지하여, 더 견고하고 일반화된 특징을 학습하도록 유도합니다. 추론이나 테스트 단계에서는 모든 뉴런이 사용되지만, 훈련 중 사용한 드롭아웃 확률에 따라 출력이 조정되어 일관된 동작을 보장합니다.
Dropout regularization helps to reduce overfitting by adding noise and promoting the learning of more diverse representations. It can improve the generalization performance of the model and make it less sensitive to small changes in the input.
드롭아웃 정규화는 노이즈를 추가하고 다양한 표현의 학습을 촉진하여 과적합을 줄이는 데 도움을 줍니다. 이는 모델의 일반화 성능을 향상시키고 입력의 작은 변화에 덜 민감하게 만들어 줄 수 있습니다.
5.4.2. Parameter Initialization
One way of addressing—or at least mitigating—the issues raised above is through careful initialization. As we will see later, additional care during optimization and suitable regularization can further enhance stability.
위에서 제기된 문제를 해결하거나 최소한 완화하는 한 가지 방법은 신중한 초기화입니다. 나중에 살펴보겠지만 최적화 및 적절한 정규화 중 추가 관리를 통해 안정성을 더욱 향상시킬 수 있습니다.
5.4.2.1. Default Initialization
In the previous sections, e.g., in Section 3.5, we used a normal distribution to initialize the values of our weights. If we do not specify the initialization method, the framework will use a default random initialization method, which often works well in practice for moderate problem sizes.
이전 섹션, 예를 들어 섹션 3.5에서 정규 분포를 사용하여 가중치 값을 초기화했습니다. 초기화 방법을 지정하지 않으면 프레임워크는 기본 임의 초기화 방법을 사용하는데, 이는 중간 정도의 문제 크기에 실제로 잘 작동합니다.
5.4.2.2. Xavier Initialization
Let’s look at the scale distribution of an output oi for some fully connected layer without nonlinearities. With nin inputs xj and their associated weights xij for this layer, an output is given by
비선형성이 없는 완전 연결 레이어에 대한 출력 oi의 스케일 분포를 살펴보겠습니다. 이 레이어에 대한 9개의 입력 xj 및 관련 가중치 xij를 사용하면 출력은 다음과 같습니다.

The weights wij are all drawn independently from the same distribution. Furthermore, let’s assume that this distribution has zero mean and variance σ2. Note that this does not mean that the distribution has to be Gaussian, just that the mean and variance need to exist. For now, let’s assume that the inputs to the layer xj also have zero mean and variance γ2 (gamma 2) and that they are independent of wij and independent of each other. In this case, we can compute the mean and variance of oi as follows:
가중치 wij는 모두 동일한 분포에서 독립적으로 그려집니다. 또한 이 분포의 평균이 0이고 분산이 σ2라고 가정해 보겠습니다. 이것은 분포가 가우시안이어야 함을 의미하는 것이 아니라 평균과 분산이 존재해야 함을 의미합니다. 지금은 계층 xj에 대한 입력도 평균과 분산 γ2(감마 2)가 0이고 wij와 서로 독립적이라고 가정해 보겠습니다. 이 경우 다음과 같이 oi의 평균과 분산을 계산할 수 있습니다.
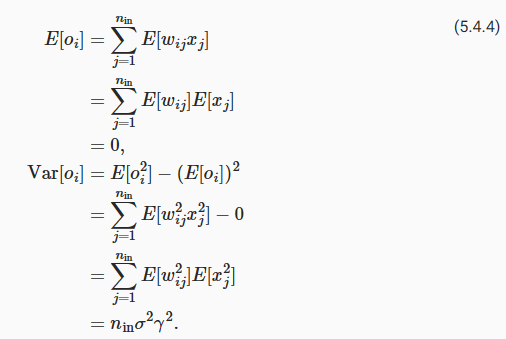
One way to keep the variance fixed is to set ninσ2=1. Now consider backpropagation. There we face a similar problem, albeit with gradients being propagated from the layers closer to the output. Using the same reasoning as for forward propagation, we see that the gradients’ variance can blow up unless noutσ2=1, where nout is the number of outputs of this layer. This leaves us in a dilemma: we cannot possibly satisfy both conditions simultaneously. Instead, we simply try to satisfy:
분산을 고정하는 한 가지 방법은 ninσ2=1로 설정하는 것입니다. 이제 역전파를 고려하십시오. 출력에 더 가까운 레이어에서 그라디언트가 전파되기는 하지만 비슷한 문제에 직면합니다. 순방향 전파와 동일한 추론을 사용하여 noutσ2=1이 아닌 한 그래디언트의 분산이 폭발할 수 있음을 알 수 있습니다. 여기서 nout은 이 레이어의 출력 수입니다. 이것은 우리를 딜레마에 빠뜨립니다. 두 조건을 동시에 만족시킬 수는 없습니다. 대신, 우리는 단순히 다음을 만족시키려고 합니다.
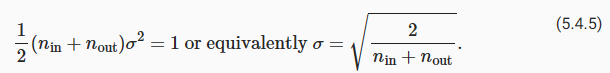
This is the reasoning underlying the now-standard and practically beneficial Xavier initialization, named after the first author of its creators (Glorot and Bengio, 2010). Typically, the Xavier initialization samples weights from a Gaussian distribution with zero mean and variance σ2=2/nin+nout. We can also adapt this to choose the variance when sampling weights from a uniform distribution. Note that the uniform distribution U(−a,a) has variance a2/3. Plugging a2/3 into our condition on σ2 yields the suggestion to initialize according to
이것은 제작자의 첫 번째 저자 이름을 따서 명명된 현재 표준적이고 실질적으로 유익한 Xavier 초기화의 기본 추론입니다(Glorot and Bengio, 2010). 일반적으로 Xavier 초기화는 평균이 0이고 분산이 σ2=2/nin+nout인 가우시안 분포에서 가중치를 샘플링합니다. 균일 분포에서 가중치를 샘플링할 때 분산을 선택하기 위해 이것을 조정할 수도 있습니다. 균일 분포 U(-a,a)의 분산은 a2/3입니다. σ2에 대한 조건에 a2/3을 연결하면 다음에 따라 초기화하라는 제안이 생성됩니다.
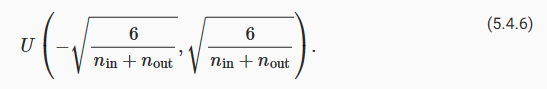
Though the assumption for nonexistence of nonlinearities in the above mathematical reasoning can be easily violated in neural networks, the Xavier initialization method turns out to work well in practice.
위의 수학적 추론에서 비선형성이 없다는 가정은 신경망에서 쉽게 위반될 수 있지만 Xavier 초기화 방법은 실제로 잘 작동하는 것으로 나타났습니다.
Xavier initialization란?
Xavier initialization, also known as Glorot initialization, is a technique used to initialize the weights of the neurons in a neural network. It aims to set the initial weights in such a way that the signal can propagate effectively through the network during both forward and backward propagation. Xavier initialization takes into account the size of the input and output of each neuron and initializes the weights from a distribution with zero mean and a specific variance.
제비어 초기화(Xavier initialization) 또는 글로럿 초기화(Glorot initialization)는 신경망의 뉴런 가중치를 초기화하는 기법입니다. 이 기법은 신경망에서 순전파와 역전파 동안 신호가 효과적으로 전파될 수 있도록 초기 가중치를 설정하는 것을 목표로 합니다. 제비어 초기화는 각 뉴런의 입력과 출력 크기를 고려하여 가중치를 평균이 0이고 특정 분산을 가진 분포에서 초기화합니다.
The intuition behind Xavier initialization is to prevent the signal from vanishing or exploding as it propagates through the network. By carefully initializing the weights, the network is more likely to converge faster and achieve better performance. It helps to address the problem of the "vanishing gradients" or "exploding gradients" that can occur in deep neural networks.
제비어 초기화의 핵심 아이디어는 신호가 신경망을 통과할 때 소멸하거나 폭발하지 않도록하는 것입니다. 가중치를 신중하게 초기화함으로써 신경망이 더 빠르게 수렴하고 더 나은 성능을 달성할 수 있습니다. 이는 깊은 신경망에서 발생할 수 있는 "소멸 그래디언트" 또는 "폭발 그래디언트" 문제를 해결하는 데 도움을 줍니다.
5.4.2.3. Beyond
The reasoning above barely scratches the surface of modern approaches to parameter initialization. A deep learning framework often implements over a dozen different heuristics. Moreover, parameter initialization continues to be a hot area of fundamental research in deep learning. Among these are heuristics specialized for tied (shared) parameters, super-resolution, sequence models, and other situations. For instance, Xiao et al. (2018) demonstrated the possibility of training 10000-layer neural networks without architectural tricks by using a carefully-designed initialization method.
위의 추론은 매개변수 초기화에 대한 최신 접근 방식의 표면을 간신히 긁어모은 것입니다. 딥 러닝 프레임워크는 종종 12개 이상의 휴리스틱을 구현합니다. 또한 매개변수 초기화는 딥 러닝의 기초 연구에서 계속해서 뜨거운 관심을 받고 있는 분야입니다. 그 중에는 연결된(공유) 매개변수, 초해상도, 시퀀스 모델 및 기타 상황에 특화된 휴리스틱이 있습니다. 예를 들어, Xiao et al. (2018)은 신중하게 설계된 초기화 방법을 사용하여 아키텍처 트릭 없이 10000층 신경망을 훈련할 수 있는 가능성을 보여주었습니다.
If the topic interests you we suggest a deep dive into this module’s offerings, reading the papers that proposed and analyzed each heuristic, and then exploring the latest publications on the topic. Perhaps you will stumble across or even invent a clever idea and contribute an implementation to deep learning frameworks.
주제에 관심이 있는 경우 이 모듈의 제안에 대해 자세히 살펴보고 각 휴리스틱을 제안하고 분석한 논문을 읽은 다음 해당 주제에 대한 최신 간행물을 탐색할 것을 제안합니다. 아마도 당신은 기발한 아이디어를 우연히 발견하거나 발명하고 딥 러닝 프레임워크 구현에 기여할 것입니다.
5.4.3. Summary
Vanishing and exploding gradients are common issues in deep networks. Great care in parameter initialization is required to ensure that gradients and parameters remain well controlled. Initialization heuristics are needed to ensure that the initial gradients are neither too large nor too small. Random initialization is key to ensure that symmetry is broken before optimization. Xavier initialization suggests that, for each layer, variance of any output is not affected by the number of inputs, and variance of any gradient is not affected by the number of outputs. ReLU activation functions mitigate the vanishing gradient problem. This can accelerate convergence.
그래디언트 소멸 및 폭발은 딥 네트워크에서 흔히 발생하는 문제입니다. 그래디언트와 매개변수가 잘 제어되도록 하려면 매개변수 초기화에 세심한 주의가 필요합니다. 초기 그래디언트가 너무 크거나 작지 않도록 초기화 휴리스틱이 필요합니다. 임의 초기화는 최적화 전에 대칭이 깨졌는지 확인하는 데 핵심입니다. Xavier 초기화는 각 레이어에 대해 출력의 분산이 입력 수의 영향을 받지 않으며 기울기의 분산이 출력 수의 영향을 받지 않음을 나타냅니다. ReLU 활성화 함수는 기울기 소실 문제를 완화합니다. 이는 수렴을 가속화할 수 있습니다.
5.4.4. Exercises
- Can you design other cases where a neural network might exhibit symmetry requiring breaking besides the permutation symmetry in an MLP’s layers?
- Can we initialize all weight parameters in linear regression or in softmax regression to the same value?
- Look up analytic bounds on the eigenvalues of the product of two matrices. What does this tell you about ensuring that gradients are well conditioned?
- If we know that some terms diverge, can we fix this after the fact? Look at the paper on layerwise adaptive rate scaling for inspiration (You et al., 2017).
'Dive into Deep Learning > D2L Multilayer Perceptrons Builder Guide' 카테고리의 다른 글
| D2L - 5.7. Predicting House Prices on Kaggle (0) | 2023.07.03 |
|---|---|
| D2L - 5.6. Dropout (0) | 2023.07.03 |
| D2L - 5.5. Generalization in Deep Learning (0) | 2023.07.03 |
| D2L - 5.3. Forward Propagation, Backward Propagation, and Computational Graphs (0) | 2023.07.02 |
| D2L - 5.2. Implementation of Multilayer Perceptrons (0) | 2023.07.01 |
| D2L - 5.1. Multilayer Perceptrons (0) | 2023.07.01 |
| D2L - 5. Multilayer Perceptrons (0) | 2023.06.30 |

