오늘의 문제는 이렇습니다.
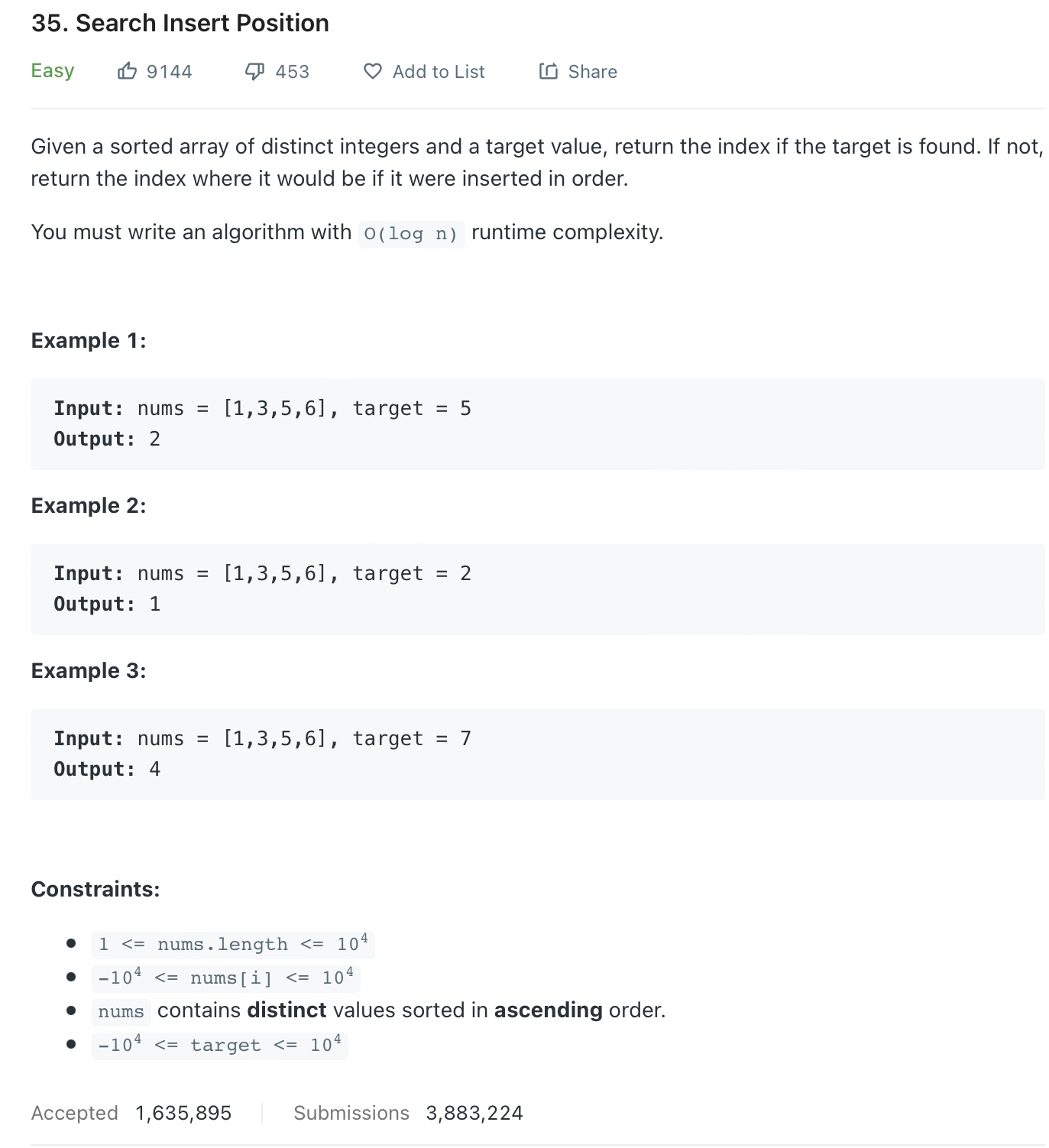
입력값은 정렬된 배열과 target 값입니다.
전형적인 Binary search 예 입니다.
Target 값을 정렬된 배열에 순서에 맞게 넣으려면 몇번째에 넣어야 하는지 그 값을 알아내는 문제 입니다.
문제에 보면 반드시 O(log n) 이라야 한다고 돼 있습니다.
우선 O(N) 인 코드를 보겠습니다.
class Solution {
public int searchInsert(int[] nums, int target) {
int resultVal = 0;
if(nums[nums.length-1] < target) { // 타겟값이 정렬된 배열의 마지막 값보다 크면 타겟값은 맨 마지막에 들어가야 함
resultVal = nums.length;
} else {
for (int i=0; i < nums.length; i++) { // 배열 갯수 만큼 루프를 돌림
if(nums[i] > target || nums[i] == target) { // 해당 값이 타겟 값보다 크거나 같으면 그 자리에 타겟 값을 넣는다.
resultVal = i; // 이 자리가 타겟 값이 들어가야 하는 자리이다.
break; // 더 이상 루프를 돌리지 않고 빠져 나간다.
}
}
}
return resultVal; // 해당 값을 반환한다.
}
}
이렇게 해도 답은 나옵니다. 그런데 이 로직을 time complexity 는 O(N) 입니다.
Time Complexity 에 대해 서는 아래 유튜브에서 아주 잘 설명 한 것 같습니다.
그러면 이 문제를 O(log n)으로 로직을 만들라는 요청에 맞게 코딩을 하면 아래와 같게 됩니다.
(Binary search를 해야 하는데요. 정렬된 배열을 다룰 때는 처음부터 끝까지 검색하지 않고 중간 값을 타겟값과 비교해서 중간 값이 작으면 오른쪽 반을 검색하고 그렇지 않으면 왼쪽 반을 검색함으로서 검색시간을 줄 이도록 하는 겁니다. 그 방법은 아래와 같습니다.)
class Solution {
public int searchInsert(int[] nums, int target) {
int pivot, left = 0, right = nums.length - 1; // 중간 값 pivot,왼쪽 값, 오른쪽 값을 담는 세가지 변수가 필요하다.
while (left <= right) { // left 가 fight 보다 작거나 같은 경우에만 while문을 돌린다.
pivot = left + (right - left) / 2; // pivot에 배열의 중간이 몇번째 인지 계산해서 넣는다.
if (nums[pivot] == target) return pivot; // 그 중간 값이 타겟 값과 같으면 그 값이 정답이 된다.
if (target < nums[pivot]) right = pivot - 1; // 중간에 위치한 값이 타깃보다 크면 왼쪽 반을 검색하기 위해서 right 값을 pivot -1로 한다.
else left = pivot + 1; // 그렇지 않으면 오른쪽 반을 검색하기 위해서 left값을 pivot + 1로 한다.
}
return left; // 마지막에 남은 값을 반환한다.
}
}
only code.
class Solution {
public int searchInsert(int[] nums, int target) {
int pivot, left = 0, right = nums.length - 1;
while (left <= right) {
pivot = left + (right - left) / 2;
if (nums[pivot] == target) return pivot;
if (target < nums[pivot]) right = pivot - 1;
else left = pivot + 1;
}
return left;
}
}
이 로직을 Python으로 할 경우 아래와 같이 된다.
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
while left <= right:
pivot = (left + right) // 2
if nums[pivot] == target:
return pivot
if target < nums[pivot]:
right = pivot - 1
else:
left = pivot + 1
return left
'etc. > Leetcode' 카테고리의 다른 글
| Leetcode 66. Plus One - Easy (0) | 2022.09.02 |
|---|---|
| Leetcode - 58. Length of Last Word - Easy (0) | 2022.08.25 |
| Leetcode - 326. Power of Three - Easy (0) | 2022.08.25 |
| Anagram - different approach with ArrayList without loop (0) | 2022.08.24 |
| Leetcode - 704. Binary Search - Easy (0) | 2022.08.22 |
| Leetcode - 28. Implement strStr() - Easy (0) | 2022.08.18 |
| Leetcode - 27. Remove Element - Easy (0) | 2022.08.18 |
| Leetcode - 26. Remove Duplicates from Sorted Array - Easy (0) | 2022.08.18 |
| Leetcode - 20. Valid Parentheses - Easy (0) | 2022.08.14 |
| Leetcode - 14. Longest Common Prefix - Easy (0) | 2022.08.11 |

