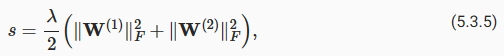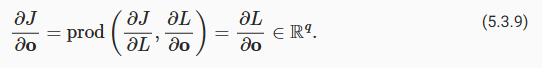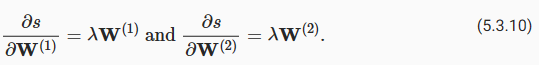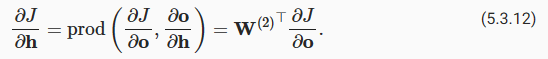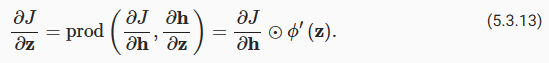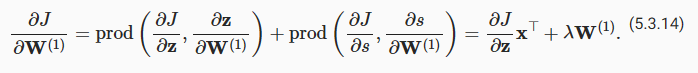5.7. Predicting House Prices on Kaggle — Dive into Deep Learning 1.0.0-beta0 documentation (d2l.ai)
5.7. Predicting House Prices on Kaggle — Dive into Deep Learning 1.0.0-beta0 documentation
d2l.ai
5.7. Predicting House Prices on Kaggle
Now that we have introduced some basic tools for building and training deep networks and regularizing them with techniques including weight decay and dropout, we are ready to put all this knowledge into practice by participating in a Kaggle competition. The house price prediction competition is a great place to start. The data is fairly generic and do not exhibit exotic structure that might require specialized models (as audio or video might). This dataset, collected by De Cock (2011), covers house prices in Ames, IA from the period of 2006–2010. It is considerably larger than the famous Boston housing dataset of Harrison and Rubinfeld (1978), boasting both more examples and more features.
딥 네트워크를 구축 및 교육하고 가중치 감쇠 및 드롭아웃을 포함한 기술로 정규화하기 위한 몇 가지 기본 도구를 도입했으므로 Kaggle 경쟁에 참여하여 이 모든 지식을 실행할 준비가 되었습니다. 집값 예측 경쟁은 시작하기에 좋은 장소입니다. 데이터는 상당히 일반적이며 특수 모델(오디오 또는 비디오처럼)이 필요할 수 있는 이국적인 구조를 나타내지 않습니다. De Cock(2011)이 수집한 이 데이터 세트는 2006~2010년 기간 동안 아이오와 주 에임스의 주택 가격을 다룹니다. 이것은 Harrison과 Rubinfeld(1978)의 유명한 보스턴 주택 데이터 세트보다 상당히 크며 더 많은 예제와 더 많은 기능을 자랑합니다.
In this section, we will walk you through details of data preprocessing, model design, and hyperparameter selection. We hope that through a hands-on approach, you will gain some intuitions that will guide you in your career as a data scientist.
이 섹션에서는 데이터 전처리, 모델 설계 및 하이퍼파라미터 선택에 대한 세부 정보를 안내합니다. 실제 접근 방식을 통해 데이터 과학자로서의 경력을 안내할 몇 가지 직관을 얻을 수 있기를 바랍니다.
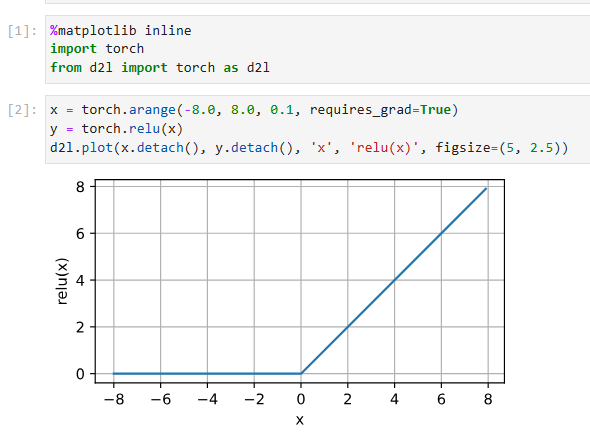
%matplotlib inline
import pandas as pd
import torch
from torch import nn
from d2l import torch as d2l
위 코드는 데이터 시각화 및 데이터 처리에 필요한 라이브러리를 가져오는 예시입니다.
- %matplotlib inline: 이 코드는 Jupyter Notebook 환경에서 matplotlib 그래프를 인라인으로 표시하도록 설정하는 명령입니다. 즉, 그래프를 코드 셀 아래에 바로 표시하도록 합니다.
- import pandas as pd: pandas는 데이터 분석과 조작에 유용한 라이브러리입니다. pd는 관례적으로 pandas를 축약형으로 사용하기 위해 사용되는 별칭(alias)입니다.
- import torch: PyTorch는 딥러닝 프레임워크로서 텐서(Tensor) 기반의 계산을 지원합니다. torch는 PyTorch 라이브러리를 임포트하는 명령입니다.
- from torch import nn: nn 모듈은 PyTorch에서 신경망 모델을 구축하기 위한 다양한 클래스와 함수를 제공합니다. torch에서 nn 모듈을 가져옵니다.
- from d2l import torch as d2l: d2l(torch)은 Dive into Deep Learning 책의 공식 코딩 스타일을 지원하는 라이브러리입니다. d2l은 관례적으로 d2l(torch)를 축약형으로 사용하기 위해 사용되는 별칭(alias)입니다.
5.7.1. Downloading Data
Throughout the book, we will train and test models on various downloaded datasets. Here, we implement two utility functions to download files and extract zip or tar files. Again, we defer their implementations into Section 23.7.
책 전반에 걸쳐 다운로드한 다양한 데이터 세트에서 모델을 훈련하고 테스트합니다. 여기서는 파일을 다운로드하고 zip 또는 tar 파일을 추출하는 두 가지 유틸리티 기능을 구현합니다. 다시 한 번 구현을 섹션 23.7로 연기합니다.
def download(url, folder, sha1_hash=None):
"""Download a file to folder and return the local filepath."""
def extract(filename, folder):
"""Extract a zip/tar file into folder."""위 코드는 파일 다운로드와 압축 해제 기능을 수행하는 함수들입니다.
- download(url, folder, sha1_hash=None): 이 함수는 주어진 URL에서 파일을 다운로드하여 지정된 폴더에 저장하고 로컬 파일 경로를 반환합니다. url은 다운로드할 파일의 URL입니다. folder는 파일을 저장할 폴더 경로입니다. sha1_hash는 선택적으로 제공되는 SHA1 해시 값으로, 다운로드한 파일의 해시 값을 확인하여 파일의 무결성을 검사할 수 있습니다.
- extract(filename, folder): 이 함수는 주어진 파일 이름의 압축 파일을 특정 폴더에 압축 해제합니다. filename은 압축 해제할 파일의 이름 또는 경로입니다. folder는 압축 해제된 파일을 저장할 폴더 경로입니다. 이 함수는 다양한 형식의 압축 파일을 지원합니다(예: zip, tar 등).
5.7.2. Kaggle
Kaggle is a popular platform that hosts machine learning competitions. Each competition centers on a dataset and many are sponsored by stakeholders who offer prizes to the winning solutions. The platform helps users to interact via forums and shared code, fostering both collaboration and competition. While leaderboard chasing often spirals out of control, with researchers focusing myopically on preprocessing steps rather than asking fundamental questions, there is also tremendous value in the objectivity of a platform that facilitates direct quantitative comparisons among competing approaches as well as code sharing so that everyone can learn what did and did not work. If you want to participate in a Kaggle competition, you will first need to register for an account (see Fig. 5.7.1).
5.7. Predicting House Prices on Kaggle — Dive into Deep Learning 1.0.0-beta0 documentation
d2l.ai
Kaggle은 기계 학습 대회를 주최하는 인기 있는 플랫폼입니다. 각 대회는 데이터 세트를 중심으로 하며 우승 솔루션에 상품을 제공하는 이해 관계자가 많은 대회를 후원합니다. 이 플랫폼은 사용자가 포럼 및 공유 코드를 통해 상호 작용하여 협업과 경쟁을 촉진하도록 돕습니다. 리더보드 추격은 종종 통제 불능 상태가 되지만 연구자들은 근본적인 질문을 하기보다 전처리 단계에 근시안적으로 초점을 맞춥니다. 또한 경쟁 접근 방식 간의 직접적인 정량적 비교와 모든 사람이 효과가 있었던 것과 그렇지 않은 것을 배우십시오. Kaggle 대회에 참가하려면 먼저 계정을 등록해야 합니다(그림 5.7.1 참조).

On the house price prediction competition page, as illustrated in Fig. 5.7.2, you can find the dataset (under the “Data” tab), submit predictions, and see your ranking, The URL is right here:
5.7. Predicting House Prices on Kaggle — Dive into Deep Learning 1.0.0-beta0 documentation
d2l.ai
주택 가격 예측 경쟁 페이지에서 그림 5.7.2와 같이 데이터 세트("데이터" 탭 아래)를 찾고 예측을 제출하고 순위를 볼 수 있습니다. URL은 바로 여기에 있습니다.
https://www.kaggle.com/c/house-prices-advanced-regression-techniques
House Prices - Advanced Regression Techniques | Kaggle
www.kaggle.com
5.7.3. Accessing and Reading the Dataset
Note that the competition data is separated into training and test sets. Each record includes the property value of the house and attributes such as street type, year of construction, roof type, basement condition, etc. The features consist of various data types. For example, the year of construction is represented by an integer, the roof type by discrete categorical assignments, and other features by floating point numbers. And here is where reality complicates things: for some examples, some data is altogether missing with the missing value marked simply as “na”. The price of each house is included for the training set only (it is a competition after all). We will want to partition the training set to create a validation set, but we only get to evaluate our models on the official test set after uploading predictions to Kaggle. The “Data” tab on the competition tab in Fig. 5.7.2 has links to download the data.
5.7. Predicting House Prices on Kaggle — Dive into Deep Learning 1.0.0-beta0 documentation
d2l.ai
competition 데이터는 훈련 및 테스트 세트로 구분됩니다. 각 레코드에는 집의 재산 가치와 거리 유형, 건축 연도, 지붕 유형, 지하실 상태 등과 같은 속성이 포함됩니다. 기능은 다양한 데이터 유형으로 구성됩니다. 예를 들어 건설 연도는 정수로, 지붕 유형은 불연속 범주 지정으로, 기타 기능은 부동 소수점 숫자로 표시됩니다. 그리고 여기에서 현실이 문제를 복잡하게 만듭니다. 일부 예의 경우 단순히 "na"로 표시된 누락된 값과 함께 일부 데이터가 완전히 누락되었습니다. 각 집의 가격은 훈련 세트에만 포함되어 있습니다 (결국 competition입니다). 훈련 세트를 분할하여 유효성 검사 세트를 만들고 싶지만 Kaggle에 예측을 업로드한 후에만 공식 테스트 세트에서 모델을 평가할 수 있습니다. 그림 5.7.2의 경쟁 탭에 있는 "데이터" 탭에는 데이터를 다운로드할 수 있는 링크가 있습니다.
To get started, we will read in and process the data using pandas, which we have introduced in Section 2.2. For convenience, we can download and cache the Kaggle housing dataset. If a file corresponding to this dataset already exists in the cache directory and its SHA-1 matches sha1_hash, our code will use the cached file to avoid clogging up your internet with redundant downloads.
시작하려면 섹션 2.2에서 소개한 pandas를 사용하여 데이터를 읽고 처리합니다. 편의를 위해 Kaggle 주택 데이터 세트를 다운로드하고 캐시할 수 있습니다. 이 데이터 세트에 해당하는 파일이 이미 캐시 디렉터리에 있고 해당 SHA-1이 sha1_hash와 일치하는 경우 코드는 캐시된 파일을 사용하여 중복 다운로드로 인터넷이 막히는 것을 방지합니다.
class KaggleHouse(d2l.DataModule):
def __init__(self, batch_size, train=None, val=None):
super().__init__()
self.save_hyperparameters()
if self.train is None:
self.raw_train = pd.read_csv(d2l.download(
d2l.DATA_URL + 'kaggle_house_pred_train.csv', self.root,
sha1_hash='585e9cc93e70b39160e7921475f9bcd7d31219ce'))
self.raw_val = pd.read_csv(d2l.download(
d2l.DATA_URL + 'kaggle_house_pred_test.csv', self.root,
sha1_hash='fa19780a7b011d9b009e8bff8e99922a8ee2eb90'))위 코드는 Kaggle House 데이터 세트를 처리하기 위한 데이터 모듈 클래스입니다.
- KaggleHouse 클래스는 d2l.DataModule 클래스를 상속합니다.
- __init__ 메서드에서는 batch_size, train, val 등의 매개변수를 받습니다.
- self.save_hyperparameters()를 호출하여 매개변수를 저장합니다.
- train이 None인 경우, pd.read_csv 함수를 사용하여 학습 데이터와 검증 데이터를 로드합니다.
- 학습 데이터는 Kaggle House 데이터 세트의 학습 세트(kaggle_house_pred_train.csv)로부터 로드합니다.
- 검증 데이터는 Kaggle House 데이터 세트의 테스트 세트(kaggle_house_pred_test.csv)로부터 로드합니다.
- 데이터를 로드하기 위해 d2l.download 함수를 사용하며, 데이터의 무결성을 검사하기 위해 SHA1 해시 값을 제공합니다.
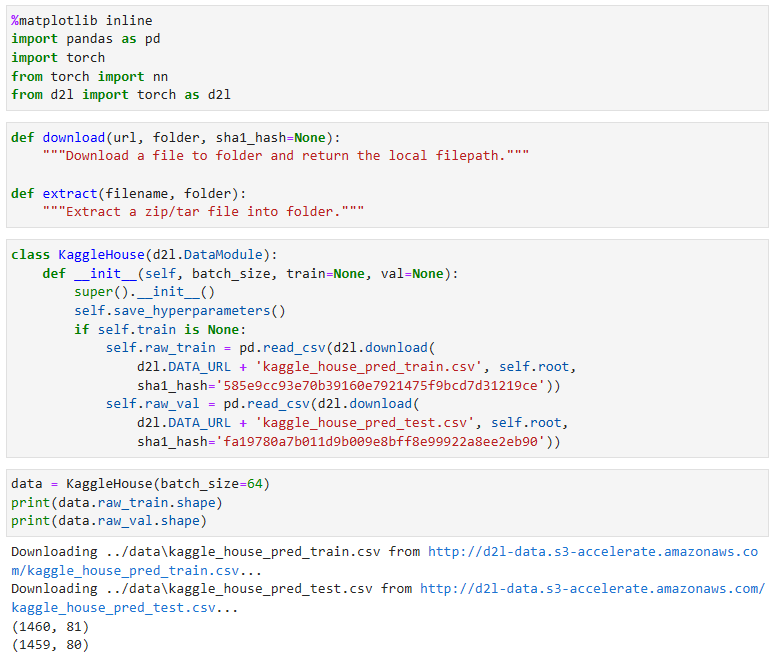
The training dataset includes 1460 examples, 80 features, and 1 label, while the validation data contains 1459 examples and 80 features.
학습 데이터 세트에는 1460개의 예, 80개의 기능 및 1개의 레이블이 포함되어 있고 검증 데이터에는 1459개의 예 및 80개의 기능이 포함되어 있습니다.
data = KaggleHouse(batch_size=64)
print(data.raw_train.shape)
print(data.raw_val.shape)
위 코드는 KaggleHouse 데이터 모듈을 사용하여 데이터를 로드하고, 로드한 데이터의 크기를 출력하는 예시입니다.
- KaggleHouse 클래스의 인스턴스인 data를 생성합니다. 이때 batch_size를 64로 지정합니다.
- data.raw_train.shape를 호출하여 학습 데이터의 크기를 출력합니다. raw_train은 pd.read_csv를 통해 로드한 학습 데이터를 의미합니다. 출력 결과는 학습 데이터의 행(row)과 열(column)의 수입니다.
- data.raw_val.shape를 호출하여 검증 데이터의 크기를 출력합니다. raw_val은 pd.read_csv를 통해 로드한 검증 데이터를 의미합니다. 출력 결과는 검증 데이터의 행(row)과 열(column)의 수입니다.
5.7.4. Data Preprocessing
Let’s take a look at the first four and last two features as well as the label (SalePrice) from the first four examples.
처음 네 가지 예의 레이블(SalePrice)뿐만 아니라 처음 네 가지 기능과 마지막 두 가지 기능을 살펴보겠습니다.
print(data.raw_train.iloc[:4, [0, 1, 2, 3, -3, -2, -1]])위 코드는 학습 데이터에서 앞부분 4개의 샘플의 특정 열(column)들을 선택하여 출력하는 예시입니다.
- data.raw_train은 로드한 학습 데이터를 나타냅니다.
- iloc[:4, [0, 1, 2, 3, -3, -2, -1]]는 학습 데이터의 첫 4개 행과 열 인덱스가 0, 1, 2, 3, -3, -2, -1인 열들을 선택하는 것을 의미합니다.
- 출력 결과는 선택한 열들로 이루어진 4개의 샘플을 표 형태로 출력합니다.
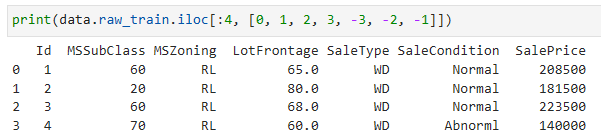
We can see that in each example, the first feature is the ID. This helps the model identify each training example. While this is convenient, it does not carry any information for prediction purposes. Hence, we will remove it from the dataset before feeding the data into the model. Besides, given a wide variety of data types, we will need to preprocess the data before we can start modeling.
각 예에서 첫 번째 feature가 ID임을 알 수 있습니다. 이렇게 하면 모델이 각 학습 예제를 식별하는 데 도움이 됩니다. 이는 편리하지만 예측 목적으로 어떤 정보도 전달하지 않습니다. 따라서 데이터를 모델에 공급하기 전에 데이터 세트에서 제거합니다. 게다가 다양한 데이터 유형이 주어지면 모델링을 시작하기 전에 데이터를 사전 처리해야 합니다.
Let’s start with the numerical features. First, we apply a heuristic, replacing all missing values by the corresponding feature’s mean. Then, to put all features on a common scale, we standardize the data by rescaling features to zero mean and unit variance:
numerical features부터 시작하겠습니다. 먼저 휴리스틱을 적용하여 누락된 모든 값을 해당 기능의 평균으로 바꿉니다. 그런 다음 모든 기능을 공통 척도에 놓기 위해 기능의 크기를 0 평균 및 단위 분산으로 재조정하여 데이터를 표준화합니다.

where μ and σ denote mean and standard deviation, respectively. To verify that this indeed transforms our feature (variable) such that it has zero mean and unit variance, note that E[x−μ/σ]=μ−μ/σ=0 and that E[(x−μ)2]=(σ2+μ2)−2μ2+μ2=σ2. Intuitively, we standardize the data for two reasons. First, it proves convenient for optimization. Second, because we do not know a priori which features will be relevant, we do not want to penalize coefficients assigned to one feature more than on any other.
여기서 μ와 σ는 각각 평균과 표준 편차를 나타냅니다. 이것이 실제로 평균이 0이고 단위 분산이 있도록 특성(변수)을 변환하는지 확인하려면 E[x−μ/σ]=μ−μ/σ=0이고 E[(x−μ)2] =(σ2+μ2)-2μ2+μ2=σ2. 직관적으로 우리는 두 가지 이유로 데이터를 표준화합니다. 첫째, 최적화에 편리합니다. 둘째, 어떤 기능이 관련될지 선험적으로 알지 못하기 때문에 한 기능에 할당된 계수에 다른 기능보다 더 많은 페널티를 주고 싶지 않습니다.
Next we deal with discrete values. This includes features such as “MSZoning”. We replace them by a one-hot encoding in the same way that we previously transformed multiclass labels into vectors (see Section 4.1.1). For instance, “MSZoning” assumes the values “RL” and “RM”. Dropping the “MSZoning” feature, two new indicator features “MSZoning_RL” and “MSZoning_RM” are created with values being either 0 or 1. According to one-hot encoding, if the original value of “MSZoning” is “RL”, then “MSZoning_RL” is 1 and “MSZoning_RM” is 0. The pandas package does this automatically for us.
다음으로 이산 값을 다룹니다. 여기에는 "MSZoning"과 같은 기능이 포함됩니다. 이전에 다중 클래스 레이블을 벡터로 변환한 것과 동일한 방식으로 원-핫 인코딩으로 대체합니다(섹션 4.1.1 참조). 예를 들어 "MSZoning"은 "RL" 및 "RM" 값을 가정합니다. "MSZoning" 기능을 삭제하면 값이 0 또는 1인 두 개의 새로운 지표 기능인 "MSZoning_RL" 및 "MSZoning_RM"이 생성됩니다. 원-핫 인코딩에 따라 "MSZoning"의 원래 값이 "RL"이면 " MSZoning_RL”은 1이고 “MSZoning_RM”은 0입니다. pandas 패키지는 이를 자동으로 수행합니다.
@d2l.add_to_class(KaggleHouse)
def preprocess(self):
# Remove the ID and label columns
label = 'SalePrice'
features = pd.concat(
(self.raw_train.drop(columns=['Id', label]),
self.raw_val.drop(columns=['Id'])))
# Standardize numerical columns
numeric_features = features.dtypes[features.dtypes!='object'].index
features[numeric_features] = features[numeric_features].apply(
lambda x: (x - x.mean()) / (x.std()))
# Replace NAN numerical features by 0
features[numeric_features] = features[numeric_features].fillna(0)
# Replace discrete features by one-hot encoding
features = pd.get_dummies(features, dummy_na=True)
# Save preprocessed features
self.train = features[:self.raw_train.shape[0]].copy()
self.train[label] = self.raw_train[label]
self.val = features[self.raw_train.shape[0]:].copy()위 코드는 KaggleHouse 클래스에 preprocess 메서드를 추가하는 예시입니다. preprocess 메서드는 데이터 전처리 과정을 수행합니다.
- self.raw_train은 원본 학습 데이터를 나타냅니다.
- self.raw_val은 원본 검증 데이터를 나타냅니다.
preprocess 메서드는 다음과 같은 과정을 거칩니다:
- ID 열과 레이블 열(SalePrice)을 제외한 나머지 특성들을 features 변수에 결합합니다.
- 숫자형 특성들을 표준화(Standardize)합니다. 숫자형 특성들은 features 변수에서 데이터 타입이 object가 아닌 열들을 선택하여 처리합니다. 각 숫자형 열의 값들을 해당 열의 평균과 표준편차를 이용하여 표준화합니다.
- 결측값(NaN)이 있는 숫자형 특성들을 0으로 대체합니다.
- 범주형 특성들을 원-핫 인코딩(one-hot encoding)합니다. dummy_na=True 옵션을 통해 결측값을 가진 특성도 처리합니다.
- 전처리된 특성들을 self.train과 self.val에 저장합니다. self.train은 전처리된 학습 데이터를 나타내며, self.val은 전처리된 검증 데이터를 나타냅니다.
이를 통해 데이터 전처리가 수행되고, 최종적으로 전처리된 학습 데이터와 검증 데이터가 self.train과 self.val에 저장됩니다.
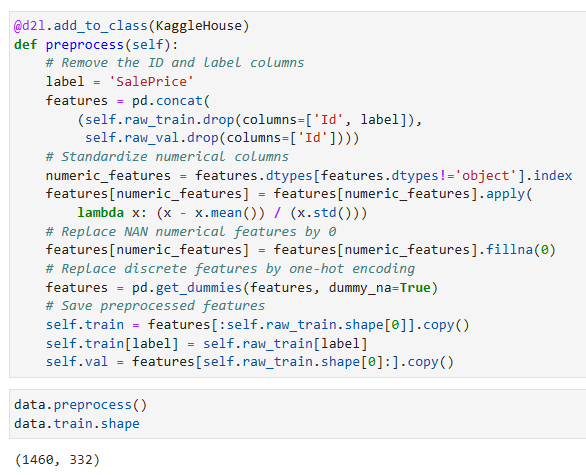
You can see that this conversion increases the number of features from 79 to 331 (excluding ID and label columns).
이 변환으로 features 수가 79개에서 331개로 증가하는 것을 볼 수 있습니다(ID 및 레이블 열 제외).
data.preprocess()
data.train.shape위 코드는 data 객체에 대해 preprocess 메서드를 호출한 후에 data.train.shape를 출력하는 예시입니다.
data.preprocess()는 앞서 설명한 preprocess 메서드를 호출하여 데이터 전처리를 수행합니다. 전처리된 데이터는 self.train에 저장됩니다.
data.train.shape는 전처리된 학습 데이터의 크기(shape)를 나타냅니다. shape는 (행의 개수, 열의 개수) 형태로 반환되며, 이 코드에서는 전처리된 학습 데이터의 행의 개수를 나타냅니다. 따라서 위 코드는 전처리된 학습 데이터의 행의 개수를 출력합니다.
5.7.5. Error Measure
To get started we will train a linear model with squared loss. Not surprisingly, our linear model will not lead to a competition-winning submission but it provides a sanity check to see whether there is meaningful information in the data. If we cannot do better than random guessing here, then there might be a good chance that we have a data processing bug. And if things work, the linear model will serve as a baseline giving us some intuition about how close the simple model gets to the best reported models, giving us a sense of how much gain we should expect from fancier models.
시작하려면 제곱 손실(squared loss)이 있는 선형 모델을 훈련합니다. 당연히 우리의 선형 모델은 경쟁에서 우승하기 위해서 제출하는 것은 아닙니다. 데이터에 의미 있는 정보가 있는지 확인하기 위해 온전한 검사를 제공합니다. 여기서 우리가 무작위 추측(random guessing)보다 더 잘할 수 없다면 거기에는 데이터 처리 버그(data processing bug)가 있을 가능성이 높습니다. 그리고 제대로 작동한다면 선형 모델은 단순한 모델이 가장 잘 report된 모델에 얼마나 근접한지에 대한 직관을 제공하는 기준선 역할을 하여 더 멋진 모델에서 얼마나 많은 이득(gain )을 기대해야 하는지에 대한 감각을 제공합니다.
With house prices, as with stock prices, we care about relative quantities more than absolute quantities. Thus we tend to care more about the relative error y−y^/y than about the absolute error y−y^. For instance, if our prediction is off by USD 100,000 when estimating the price of a house in Rural Ohio, where the value of a typical house is 125,000 USD, then we are probably doing a horrible job. On the other hand, if we err by this amount in Los Altos Hills, California, this might represent a stunningly accurate prediction (there, the median house price exceeds 4 million USD).
주택 가격은 주식 가격과 마찬가지로 절대 수량보다 상대적 수량에 더 많은 관심을 기울입니다. 따라서 절대 오차 y−y^보다 상대 오차 y−y^/y에 더 신경을 쓰는 경향이 있습니다. 예를 들어, 일반적인 주택 가격이 125,000 USD인 시골 오하이오의 주택 가격을 추정할 때 예측이 USD 100,000만큼 빗나간다면 우리는 아마도 끔찍한 일을 하고 있는 것입니다. 반면에 캘리포니아의 로스 알토스 힐스에서 이 금액만큼 오류가 발생하면 놀라울 정도로 정확한 예측이 될 수 있습니다(거기 주택 중간 가격이 400만 달러를 초과함).
One way to address this problem is to measure the discrepancy in the logarithm of the price estimates. In fact, this is also the official error measure used by the competition to evaluate the quality of submissions. After all, a small value δ for |log y−log y^|≤δ translates into e−δ≤y^/y≤eδ. This leads to the following root-mean-squared-error between the logarithm of the predicted price and the logarithm of the label price:

@d2l.add_to_class(KaggleHouse)
def get_dataloader(self, train):
label = 'SalePrice'
data = self.train if train else self.val
if label not in data: return
get_tensor = lambda x: torch.tensor(x.values, dtype=torch.float32)
# Logarithm of prices
tensors = (get_tensor(data.drop(columns=[label])), # X
torch.log(get_tensor(data[label])).reshape((-1, 1))) # Y
return self.get_tensorloader(tensors, train)위 코드는 get_dataloader라는 메서드를 KaggleHouse 클래스에 추가하는 예시입니다.
get_dataloader 메서드는 train 매개변수를 통해 학습 데이터 또는 검증 데이터에 대한 데이터 로더를 반환합니다. 메서드 내부에서는 label이라는 변수에 'SalePrice'를 할당하고, train이 True인 경우 self.train을 데이터로 선택하고, False인 경우 self.val을 데이터로 선택합니다.
그 후, get_tensor라는 람다 함수를 정의하여 데이터를 torch.tensor 형태로 변환합니다. get_tensor 함수는 데이터의 값을 torch.float32 자료형으로 변환하여 반환합니다.
마지막으로, tensors 변수에는 입력 데이터 X와 목표 데이터 Y가 포함된 튜플이 저장됩니다. X는 data에서 label 열을 제외한 값들을 torch.tensor로 변환한 것이고, Y는 data의 label 열을 로그 변환하여 torch.tensor로 변환한 것입니다. 이후, tensors를 이용하여 데이터 로더를 생성하고 반환합니다.
5.7.6. K-Fold Cross-Validation
You might recall that we introduced cross-validation in Section 3.6.3, where we discussed how to deal with model selection. We will put this to good use to select the model design and to adjust the hyperparameters. We first need a function that returns the i th fold of the data in a K-fold cross-validation procedure. It proceeds by slicing out the i th segment as validation data and returning the rest as training data. Note that this is not the most efficient way of handling data and we would definitely do something much smarter if our dataset was considerably larger. But this added complexity might obfuscate our code unnecessarily so we can safely omit it here owing to the simplicity of our problem.
모델 선택을 처리하는 방법에 대해 논의한 섹션 3.6.3에서 교차 검증을 소개한 것을 기억할 것입니다. 모델 설계를 선택하고 하이퍼파라미터를 조정하는 데 유용하게 사용할 것입니다. 먼저 K-폴드 교차 검증 절차에서 데이터의 i번째 폴드를 반환하는 함수가 필요합니다. i 번째 세그먼트를 유효성 검사 데이터로 잘라내고 나머지는 교육 데이터로 반환하는 방식으로 진행됩니다. 이것은 데이터를 처리하는 가장 효율적인 방법이 아니며 데이터 세트가 상당히 더 큰 경우 확실히 훨씬 더 스마트한 작업을 수행할 것입니다. 그러나이 추가 된 복잡성은 코드를 불필요하게 난독화할 수 있으므로 문제의 단순성으로 인해 여기에서 안전하게 생략할 수 있습니다.
def k_fold_data(data, k):
rets = []
fold_size = data.train.shape[0] // k
for j in range(k):
idx = range(j * fold_size, (j+1) * fold_size)
rets.append(KaggleHouse(data.batch_size, data.train.drop(index=idx),
data.train.loc[idx]))
return rets위 코드는 k_fold_data라는 함수입니다. 이 함수는 데이터를 K-fold 교차 검증을 위해 K개의 폴드로 나누는 기능을 수행합니다.
k_fold_data 함수는 data와 k라는 두 개의 매개변수를 받습니다. 여기서 data는 KaggleHouse 클래스의 객체이며, k는 폴드의 개수를 나타냅니다.
함수 내부에서는 빈 리스트인 rets를 생성합니다. fold_size 변수에는 데이터의 학습 세트 크기를 K로 나눈 값이 저장됩니다. 그런 다음, range(k)를 반복하면서 폴드마다 인덱스를 생성합니다. 인덱스는 j * fold_size에서 (j+1) * fold_size까지의 범위로 생성됩니다.
마지막으로, rets 리스트에는 KaggleHouse 객체를 생성하여 추가합니다. 이때, 데이터의 배치 크기는 동일하게 유지되고, data.train에서 생성한 인덱스를 제외한 데이터를 학습 데이터로 사용하고, 해당 인덱스만을 가진 데이터를 검증 데이터로 사용합니다. 이 과정을 K번 반복하고, 최종적으로 rets 리스트에는 K개의 KaggleHouse 객체가 저장되어 반환됩니다.
The average validation error is returned when we train K times in the K-fold cross-validation.
K-겹 교차 검증에서 K번 훈련할 때 평균 검증 오류가 반환됩니다.
def k_fold(trainer, data, k, lr):
val_loss, models = [], []
for i, data_fold in enumerate(k_fold_data(data, k)):
model = d2l.LinearRegression(lr)
model.board.yscale='log'
if i != 0: model.board.display = False
trainer.fit(model, data_fold)
val_loss.append(float(model.board.data['val_loss'][-1].y))
models.append(model)
print(f'average validation log mse = {sum(val_loss)/len(val_loss)}')
return models위 코드는 k_fold라는 함수입니다. 이 함수는 K-fold 교차 검증을 수행하여 모델을 학습하고, 각 폴드에서의 검증 손실과 학습된 모델을 반환합니다.
k_fold 함수는 trainer, data, k, lr 네 개의 매개변수를 받습니다. trainer는 학습을 담당하는 Trainer 객체, data는 KaggleHouse 객체, k는 폴드의 개수, lr은 학습률을 의미합니다.
함수 내부에서는 val_loss와 models라는 빈 리스트를 생성합니다. 이후, k_fold_data 함수를 호출하여 data 객체를 K개의 폴드로 나눕니다. 이때, 각 폴드마다 KaggleHouse 객체가 생성되고, data_fold에 저장됩니다.
그 다음, 반복문을 통해 각 폴드에 대해 모델을 학습합니다. 첫 번째 폴드에서는 model.board.display를 True로 설정하여 학습 과정을 출력하고, 이후 폴드에서는 출력을 생략하기 위해 model.board.display를 False로 설정합니다. trainer.fit 함수를 사용하여 모델을 학습하고, 검증 손실을 val_loss 리스트에 추가하고, 학습된 모델을 models 리스트에 추가합니다.
모든 폴드에 대한 학습이 완료되면, val_loss 리스트의 값들을 평균하여 평균 검증 손실을 출력합니다. 마지막으로, 학습된 모델들을 반환합니다.
5.7.7. Model Selection
In this example, we pick an untuned set of hyperparameters and leave it up to the reader to improve the model. Finding a good choice can take time, depending on how many variables one optimizes over. With a large enough dataset, and the normal sorts of hyperparameters, K-fold cross-validation tends to be reasonably resilient against multiple testing. However, if we try an unreasonably large number of options we might just get lucky and find that our validation performance is no longer representative of the true error.
이 예에서는 조정되지 않은 하이퍼파라미터 세트를 선택하고 모델을 개선하기 위해 독자에게 맡깁니다. 얼마나 많은 변수를 최적화하느냐에 따라 좋은 선택을 찾는 데 시간이 걸릴 수 있습니다. 충분히 큰 데이터 세트와 일반적인 종류의 하이퍼파라미터를 사용하면 K-겹 교차 검증은 여러 테스트에 대해 합리적으로 탄력적인 경향이 있습니다. 그러나 비합리적으로 많은 수의 옵션을 시도하면 운이 좋아 검증 성능이 더 이상 실제 오류를 나타내지 않는다는 것을 알게 될 수 있습니다.
trainer = d2l.Trainer(max_epochs=10)
models = k_fold(trainer, data, k=5, lr=0.01)위 코드는 d2l.Trainer 객체를 생성하고, 이를 사용하여 k_fold 함수를 호출하는 부분입니다.
d2l.Trainer 객체는 학습을 관리하는 역할을 담당합니다. 생성자의 매개변수 max_epochs는 최대 학습 에포크 수를 나타내며, 이 경우 10으로 설정되어 있습니다.
k_fold 함수는 앞서 설명한 대로 K-fold 교차 검증을 수행하여 모델을 학습하고, 학습된 모델들을 반환합니다. 이때, trainer 객체를 첫 번째 매개변수로 전달하고, 두 번째 매개변수로는 데이터셋인 data 객체를 전달합니다. k는 폴드의 개수로 설정되어 있으며, lr은 학습률을 의미합니다.
models 변수는 k_fold 함수에서 반환된 학습된 모델들을 저장하는 리스트입니다.
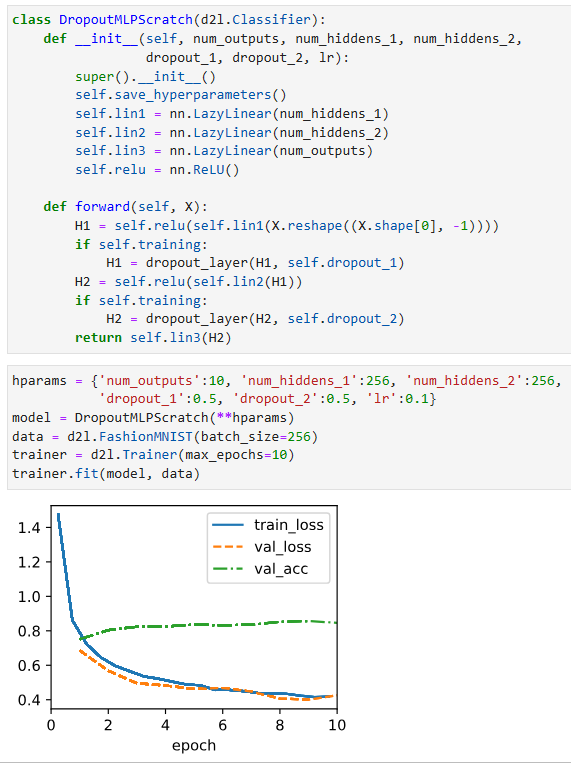
* 로컬 결과
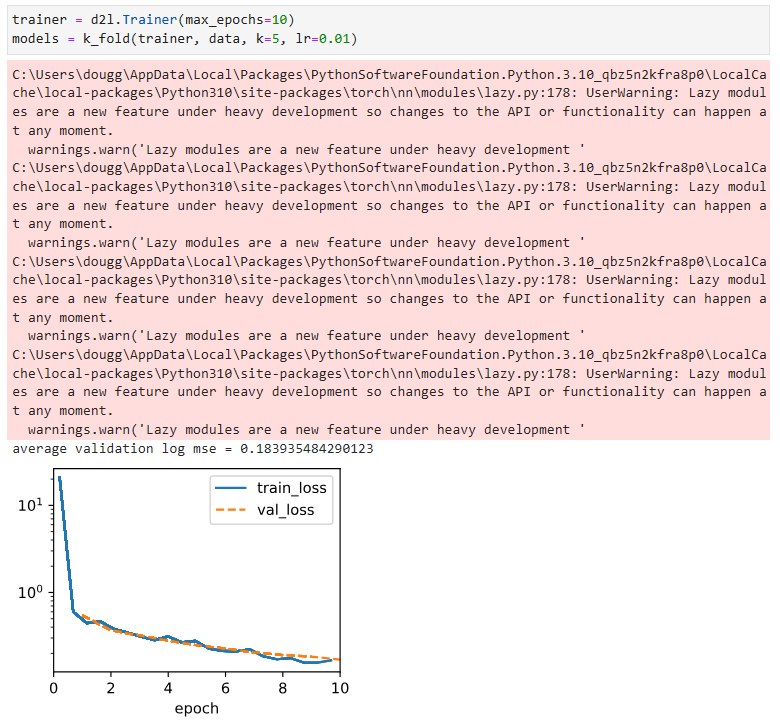
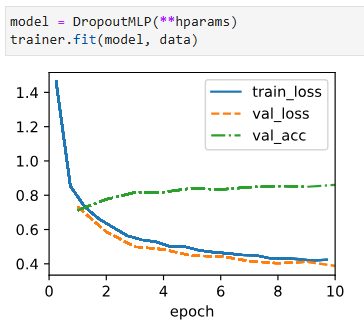
* 교재 결과
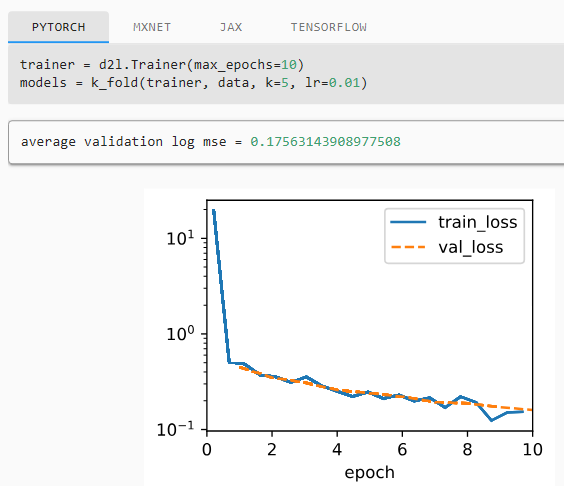
Notice that sometimes the number of training errors for a set of hyperparameters can be very low, even as the number of errors on K-fold cross-validation is considerably higher. This indicates that we are overfitting. Throughout training you will want to monitor both numbers. Less overfitting might indicate that our data can support a more powerful model. Massive overfitting might suggest that we can gain by incorporating regularization techniques.
K-겹 교차 검증의 오류 수가 상당히 높은 경우에도 하이퍼 매개변수 세트에 대한 훈련 오류 수가 때때로 매우 낮을 수 있다는 점에 유의하십시오. 이것은 우리가 과적합되고 있음을 나타냅니다. 교육 내내 두 숫자를 모두 모니터링하고 싶을 것입니다. 과적합이 적으면 데이터가 더 강력한 모델을 지원할 수 있음을 나타낼 수 있습니다. 대규모 과적합은 정규화 기술을 통합하여 얻을 수 있음을 시사할 수 있습니다.
5.7.8. Submitting Predictions on Kaggle
Now that we know what a good choice of hyperparameters should be, we might calculate the average predictions on the test set by all the K models. Saving the predictions in a csv file will simplify uploading the results to Kaggle. The following code will generate a file called submission.csv.
이제 우리는 하이퍼파라미터의 좋은 선택이 무엇인지 알았으므로 모든 K 모델에 의해 테스트 세트에 대한 평균 예측을 계산할 수 있습니다. csv 파일에 예측을 저장하면 결과를 Kaggle에 간단하게 업로드할 수 있습니다. 다음 코드는 submit.csv라는 파일을 생성합니다.
preds = [model(torch.tensor(data.val.values, dtype=torch.float32))
for model in models]
# Taking exponentiation of predictions in the logarithm scale
ensemble_preds = torch.exp(torch.cat(preds, 1)).mean(1)
submission = pd.DataFrame({'Id':data.raw_val.Id,
'SalePrice':ensemble_preds.detach().numpy()})
submission.to_csv('submission.csv', index=False)위 코드는 앙상블 모델을 사용하여 예측을 수행하고, 예측 결과를 제출용 CSV 파일로 저장하는 부분입니다.
preds는 앙상블에 사용할 모델들을 순회하면서 검증 데이터셋(data.val)에 대한 예측을 수행한 결과를 저장하는 리스트입니다. 예측 결과는 각 모델에 대해 torch.tensor를 사용하여 입력 데이터를 전달하여 계산되고, 이를 리스트에 추가합니다.
ensemble_preds는 preds 리스트에 저장된 예측 결과를 가지고 앙상블 예측을 수행한 결과입니다. 여기서는 예측 결과를 로그 스케일에서 다시 원래 스케일로 변환하기 위해 지수 함수(torch.exp)를 적용하고, torch.cat 함수를 사용하여 예측 결과를 열 방향으로 연결한 후 평균(mean(1))을 계산합니다. 최종 앙상블 예측은 평균값으로 구해집니다.
submission은 예측 결과를 저장하기 위한 DataFrame 객체입니다. data.raw_val.Id는 제출할 데이터의 ID 열을 나타내고, ensemble_preds.detach().numpy()는 앙상블 예측 결과를 넘파이 배열로 변환한 값으로 SalePrice 열을 나타냅니다.
마지막으로, submission을 CSV 파일로 저장하여 제출용 파일인 'submission.csv'로 저장합니다. index=False는 인덱스를 저장하지 않도록 설정하는 옵션입니다.
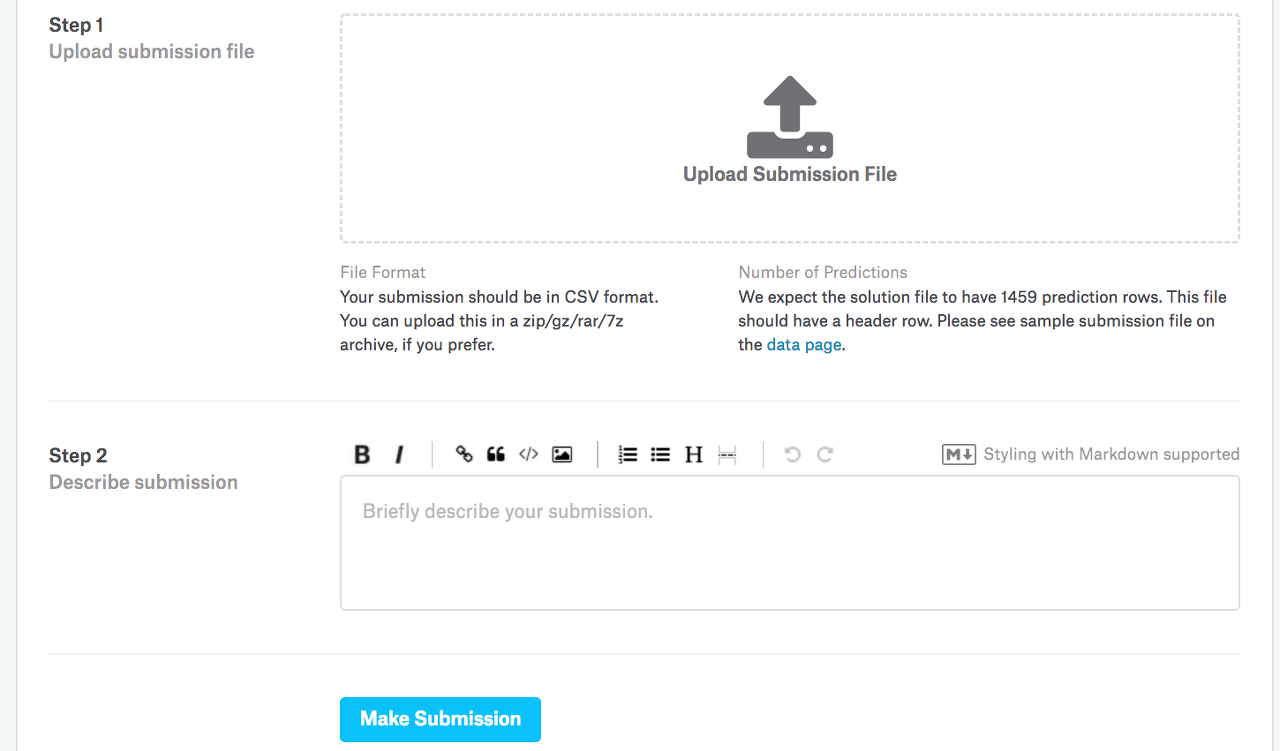
Next, as demonstrated in Fig. 5.7.3, we can submit our predictions on Kaggle and see how they compare with the actual house prices (labels) on the test set. The steps are quite simple:
다음으로 그림 5.7.3에 나와 있는 것처럼 Kaggle에 대한 예측을 제출하고 테스트 세트의 실제 주택 가격(라벨)과 비교하는 방법을 확인할 수 있습니다. 단계는 매우 간단합니다.
- Log in to the Kaggle website and visit the house price prediction competition page.
- Kaggle 웹 사이트에 로그인하고 집값 예측 경쟁 페이지를 방문하십시오.
- Click the “Submit Predictions” or “Late Submission” button (as of this writing, the button is located on the right).
- "예측 제출" 또는 "늦은 제출" 버튼을 클릭합니다(이 글을 쓰는 시점에서 버튼은 오른쪽에 있음).
- Click the “Upload Submission File” button in the dashed box at the bottom of the page and select the prediction file you wish to upload.
- 페이지 하단의 점선 상자에서 "제출 파일 업로드" 버튼을 클릭하고 업로드할 예측 파일을 선택합니다.
- Click the “Make Submission” button at the bottom of the page to view your results.
- 결과를 보려면 페이지 하단에 있는 "제출하기" 버튼을 클릭하십시오.
5.7.9. Summary
Real data often contains a mix of different data types and needs to be preprocessed. Rescaling real-valued data to zero mean and unit variance is a good default. So is replacing missing values with their mean. Besides, transforming categorical features into indicator features allows us to treat them like one-hot vectors. When we tend to care more about the relative error than about the absolute error, we can measure the discrepancy in the logarithm of the prediction. To select the model and adjust the hyperparameters, we can use K-fold cross-validation .
실제 데이터에는 다양한 데이터 유형이 혼합되어 있는 경우가 많으며 사전 처리가 필요합니다. 실수 값 데이터를 0 평균 및 단위 분산으로 재조정하는 것이 좋은 기본값입니다. 누락된 값을 평균으로 대체하는 것도 마찬가지입니다. 게다가 범주형 기능을 지표 기능으로 변환하면 원-핫 벡터처럼 처리할 수 있습니다. 절대 오차보다 상대 오차에 더 신경을 쓰는 경향이 있을 때 예측 로그의 불일치를 측정할 수 있습니다. 모델을 선택하고 하이퍼파라미터를 조정하기 위해 K-겹 교차 검증을 사용할 수 있습니다.
5.7.10. Exercises
- Submit your predictions for this section to Kaggle. How good are your predictions?
- Is it always a good idea to replace missing values by their mean? Hint: can you construct a situation where the values are not missing at random?
- Improve the score on Kaggle by tuning the hyperparameters through K-fold cross-validation.
- Improve the score by improving the model (e.g., layers, weight decay, and dropout).
- What happens if we do not standardize the continuous numerical features like what we have done in this section?
'Dive into Deep Learning > D2L Multilayer Perceptrons Builder Guide' 카테고리의 다른 글
| D2L - 5.6. Dropout (0) | 2023.07.03 |
|---|---|
| D2L - 5.5. Generalization in Deep Learning (0) | 2023.07.03 |
| D2L - 5.4. Numerical Stability and Initialization (0) | 2023.07.02 |
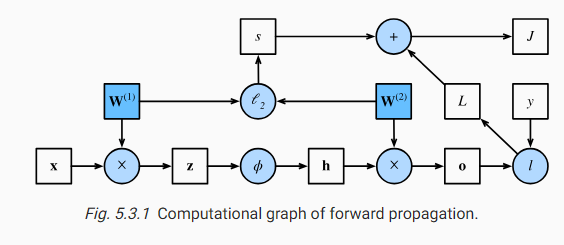
| D2L - 5.3. Forward Propagation, Backward Propagation, and Computational Graphs (0) | 2023.07.02 |
| D2L - 5.2. Implementation of Multilayer Perceptrons (0) | 2023.07.01 |
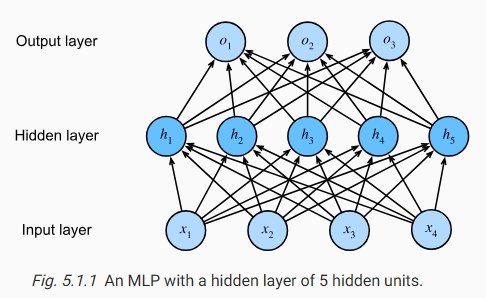
| D2L - 5.1. Multilayer Perceptrons (0) | 2023.07.01 |
| D2L - 5. Multilayer Perceptrons (0) | 2023.06.30 |