D2L - 5.6. Dropout
2023. 7. 3. 05:06 |
5.6. Dropout — Dive into Deep Learning 1.0.0-beta0 documentation (d2l.ai)
5.6. Dropout — Dive into Deep Learning 1.0.0-beta0 documentation
d2l.ai
5.6. Dropout
Let’s think briefly about what we expect from a good predictive model. We want it to peform well on unseen data. Classical generalization theory suggests that to close the gap between train and test performance, we should aim for a simple model. Simplicity can come in the form of a small number of dimensions. We explored this when discussing the monomial basis functions of linear models in Section 3.6. Additionally, as we saw when discussing weight decay (ℓ2 regularization) in Section 3.7, the (inverse) norm of the parameters also represents a useful measure of simplicity. Another useful notion of simplicity is smoothness, i.e., that the function should not be sensitive to small changes to its inputs. For instance, when we classify images, we would expect that adding some random noise to the pixels should be mostly harmless.
좋은 예측 모델에서 기대하는 바에 대해 간단히 생각해 봅시다. 우리는 그것이 보이지 않는 데이터에서 잘 작동하기를 원합니다. 고전적 일반화 이론은 학습과 테스트 성능 사이의 격차를 좁히기 위해 간단한 모델을 목표로 해야 한다고 제안합니다. 단순성은 차원 수가 적다는 형태로 나타날 수 있습니다. 우리는 섹션 3.6에서 선형 모델의 단항 기저 함수를 논의할 때 이것을 탐구했습니다. 또한 섹션 3.7에서 가중치 감쇠(ℓ2 정규화)를 논의할 때 보았듯이 매개변수의 (역) 규범도 단순성의 유용한 척도를 나타냅니다. 단순함의 또 다른 유용한 개념은 매끄러움입니다. 즉, 함수는 입력의 작은 변화에 민감하지 않아야 합니다. 예를 들어 이미지를 분류할 때 픽셀에 임의의 노이즈를 추가해도 대부분 무해할 것으로 예상합니다.
In 1995, Christopher Bishop formalized this idea when he proved that training with input noise is equivalent to Tikhonov regularization (Bishop, 1995). This work drew a clear mathematical connection between the requirement that a function be smooth (and thus simple), and the requirement that it be resilient to perturbations in the input.
1995년 Christopher Bishop은 입력 노이즈를 사용한 훈련이 Tikhonov 정규화와 동일하다는 것을 증명하면서 이 아이디어를 공식화했습니다(Bishop, 1995). 이 작업은 함수가 매끄럽고(따라서 단순해야 함) 요구 사항과 입력의 섭동(perturbations, 혼란, 동요, 당황)에 탄력적이어야 한다는 요구 사항 사이에 명확한 수학적 연결을 그렸습니다.
Then, in 2014, Srivastava et al. (2014) developed a clever idea for how to apply Bishop’s idea to the internal layers of a network, too. Their idea, called dropout, involves injecting noise while computing each internal layer during forward propagation, and it has become a standard technique for training neural networks. The method is called dropout because we literally drop out some neurons during training. Throughout training, on each iteration, standard dropout consists of zeroing out some fraction of the nodes in each layer before calculating the subsequent layer.
그런 다음 2014년 Srivastava et al. (2014)는 Bishop의 아이디어를 네트워크의 내부 계층에도 적용하는 방법에 대한 기발한 아이디어를 개발했습니다. 드롭아웃(dropout)이라고 하는 그들의 아이디어는 정방향 전파(forward propagation) 동안 각 내부 레이어를 계산하는 동안 노이즈를 주입하는 것과 관련이 있으며, 신경망 훈련을 위한 표준 기술이 되었습니다. 이 방법을 드롭아웃이라고 부르는 이유는 말 그대로 훈련 중에 일부 뉴런을 드롭아웃하기 때문입니다. 교육 전반에 걸쳐 각 반복에서 표준 드롭아웃은 후속 계층을 계산하기 전에 각 계층의 노드 일부를 0으로 만드는 것으로 구성됩니다.
Dropout이란?
Dropout is a regularization technique commonly used in machine learning, particularly in neural networks, to prevent overfitting and improve generalization performance. It involves randomly dropping out (setting to zero) a proportion of the neurons or connections in a neural network during training.
Dropout은 머신 러닝에서 흔히 사용되는 정규화 기법으로, 특히 신경망에서 과적합을 방지하고 일반화 성능을 향상시키는 데 사용됩니다. 학습 중에 신경망의 일부 뉴런이나 연결을 무작위로 비활성화(0으로 설정)하는 것이 특징입니다.
During each training iteration, dropout randomly masks (sets to zero) a certain fraction of the neurons or connections in a layer, effectively removing them from the network temporarily. This forces the network to learn with a reduced set of neurons and prevents individual neurons from relying too heavily on specific features or co-adapting with other neurons.
각 학습 반복에서 Dropout은 무작위로 일부 뉴런이나 연결을 마스킹하여 (0으로 설정하여) 신경망에서 임시로 제거합니다. 이렇게 함으로써 신경망은 줄어든 뉴런 집합을 사용하여 학습하게 되며, 개별 뉴런이 특정 특징에 지나치게 의존하거나 다른 뉴런과 공동으로 적응하는 것을 방지합니다.
By randomly dropping out neurons, dropout introduces noise and prevents the neural network from relying too heavily on any particular subset of neurons. This encourages the network to learn more robust and generalizable representations of the data.
Dropout은 무작위로 뉴런을 제거함으로써 노이즈를 도입하고, 신경망이 특정 뉴런 집합에 지나치게 의존하지 않도록 합니다. 이는 신경망이 더 견고하고 일반화 가능한 데이터 표현을 학습하도록 장려합니다.
During inference or testing, dropout is typically turned off, and the full network is used for making predictions.
추론이나 테스트 단계에서는 일반적으로 Dropout을 끄고 전체 네트워크를 사용하여 예측을 수행합니다.
To be clear, we are imposing our own narrative with the link to Bishop. The original paper on dropout offers intuition through a surprising analogy to sexual reproduction. The authors argue that neural network overfitting is characterized by a state in which each layer relies on a specific pattern of activations in the previous layer, calling this condition co-adaptation. dropout, they claim, breaks up co-adaptation just as sexual reproduction is argued to break up co-adapted genes. While the explanatory of this theory is certainly up for debate, the dropout technique itself has proved enduring, and various forms of dropout are implemented in most deep learning libraries.
명확히 하기 위해 우리는 Bishop에 대한 링크로 우리 자신의 내러티브를 부과하고 있습니다. dropout 에 관한 원본 논문은 유성 생식에 대한 놀라운 비유를 통해 직관을 제공합니다. 저자는 신경망 과적합이 각 계층이 이전 계층의 특정 활성화 패턴에 의존하는 상태를 특징으로 하며 이 조건을 공동 적응(co-adaptation)이라고 합니다. 그들은 유성 생식이 공동 적응된 유전자를 분열시킨다고 주장하듯이 중퇴는 공동 적응을 분열시킨다고 주장한다. 이 이론에 대한 설명은 확실히 논쟁의 여지가 있지만 드롭아웃 기술 자체는 오래 지속되는 것으로 입증되었으며 다양한 형태의 드롭아웃이 대부분의 딥 러닝 라이브러리에서 구현됩니다.
The key challenge is how to inject this noise. One idea is to inject the noise in an unbiased manner so that the expected value of each layer—while fixing the others—equals to the value it would have taken absent noise. In Bishop’s work, he added Gaussian noise to the inputs to a linear model. At each training iteration, he added noise sampled from a distribution with mean zero ϵ∼N(0,σ2) to the input x, yielding a perturbed point x′=x+ϵ. In expectation, E[x′]=x.
핵심 과제는 이 노이즈를 주입하는 방법입니다. 한 가지 아이디어는 편향되지 않은 방식으로 노이즈를 주입하여 각 레이어의 예상 값이 다른 레이어를 수정하는 동안 노이즈가 없는 값과 같도록 하는 것입니다. Bishop의 작업에서 그는 선형 모델의 입력에 가우시안 노이즈를 추가했습니다. 각 훈련 반복에서 그는 평균 0 ϵ~N(0,σ2)인 분포에서 샘플링된 노이즈를 입력 x에 추가하여 교란된 점 x′=x+ϵ를 산출했습니다. 예상대로 E[x′]=x.
In standard dropout regularization, one zeros out some fraction of the nodes in each layer and then debiases each layer by normalizing by the fraction of nodes that were retained (not dropped out). In other words, with dropout probability p, each intermediate activation ℎ is replaced by a random variable ℎ′ as follows:
표준 드롭아웃 정규화에서는 각 레이어의 일부 노드를 0으로 만든 다음 유지된(드롭아웃이 아닌) 노드의 일부로 정규화하여 각 레이어의 편향성을 제거합니다. 즉, 드롭아웃 확률이 p인 경우 각 중간 활성화 ℎ는 다음과 같이 임의 변수 ℎ'로 대체됩니다.
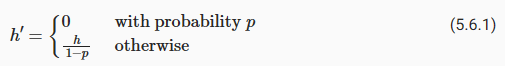
By design, the expectation remains unchanged, i.e., E[ℎ′]=ℎ.
설계상 기대치는 변하지 않습니다. 즉, E[ℎ′]=ℎ입니다.
import torch
from torch import nn
from d2l import torch as d2l위 코드는 torch, torch.nn, 그리고 d2l 패키지를 임포트하는 예시입니다.
- torch: PyTorch의 기본 패키지로, 다양한 텐서 연산과 딥러닝 모델 구성을 위한 도구들을 제공합니다.
- torch.nn: PyTorch의 신경망 관련 모듈을 포함한 패키지로, 신경망 레이어, 활성화 함수, 손실 함수 등을 정의하고 제공합니다.
- d2l.torch: d2l 패키지에서 제공하는 PyTorch 관련 유틸리티 함수와 클래스들을 포함한 모듈입니다. 이 모듈은 d2l 패키지의 torch 모듈에 대한 별칭(Alias)로 사용됩니다.
해당 코드에서는 이러한 패키지와 모듈을 임포트하여 사용할 준비를 하고 있습니다. 이후 코드에서는 해당 패키지와 모듈의 함수와 클래스를 사용하여 신경망 모델을 정의하고 학습하는 등의 작업을 수행할 수 있습니다.
5.6.1. Dropout in Practice
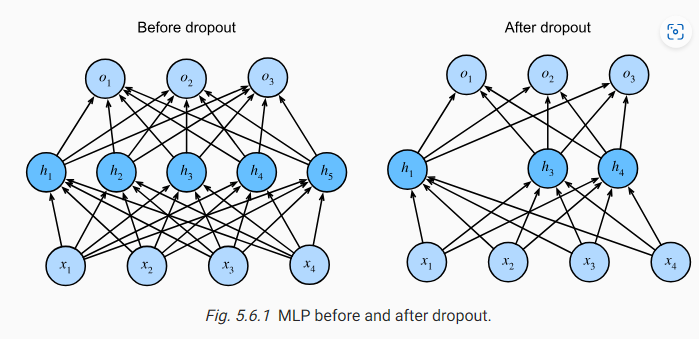
Recall the MLP with a hidden layer and 5 hidden units in Fig. 5.1.1. When we apply dropout to a hidden layer, zeroing out each hidden unit with probability p, the result can be viewed as a network containing only a subset of the original neurons. In Fig. 5.6.1, ℎ2 and ℎ5 are removed. Consequently, the calculation of the outputs no longer depends on ℎ2 or ℎ5 and their respective gradient also vanishes when performing backpropagation. In this way, the calculation of the output layer cannot be overly dependent on any one element of ℎ1,…,ℎ5.
그림 5.1.1에서 은닉층과 5개의 은닉 유닛이 있는 MLP를 상기하십시오. 은닉층에 드롭아웃을 적용하여 각 은닉 유닛을 확률 p로 제로화하면 결과는 원래 뉴런의 하위 집합만 포함하는 네트워크로 볼 수 있습니다. 그림 5.6.1에서 ℎ2와 ℎ5는 제거되었다. 결과적으로 출력 계산은 더 이상 ℎ2 또는 ℎ5에 의존하지 않으며 역전파를 수행할 때 각 기울기도 사라집니다. 이와 같이 출력 레이어의 계산은 ℎ1,…,ℎ5 중 어느 하나의 요소에 지나치게 의존할 수 없습니다.
Typically, we disable dropout at test time. Given a trained model and a new example, we do not drop out any nodes and thus do not need to normalize. However, there are some exceptions: some researchers use dropout at test time as a heuristic for estimating the uncertainty of neural network predictions: if the predictions agree across many different dropout masks, then we might say that the network is more confident.
일반적으로 테스트 시 드롭아웃을 비활성화합니다. 훈련된 모델과 새 예제가 주어지면 노드를 삭제하지 않으므로 정규화할 필요가 없습니다. 그러나 몇 가지 예외가 있습니다. 일부 연구원은 신경망 예측의 불확실성을 추정하기 위한 휴리스틱으로 테스트 시간에 드롭아웃을 사용합니다. 여러 다른 드롭아웃 마스크에서 예측이 일치하면 네트워크가 더 확실하다고 말할 수 있습니다.
5.6.2. Implementation from Scratch
To implement the dropout function for a single layer, we must draw as many samples from a Bernoulli (binary) random variable as our layer has dimensions, where the random variable takes value 1 (keep) with probability 1−p and 0 (drop) with probability p. One easy way to implement this is to first draw samples from the uniform distribution U[0,1]. Then we can keep those nodes for which the corresponding sample is greater than p, dropping the rest.
단일 레이어에 대한 드롭아웃 기능을 구현하려면 레이어가 갖는 차원만큼 Bernoulli(이진) 랜덤 변수에서 많은 샘플을 가져와야 합니다. 여기서 랜덤 변수는 확률 1-p 및 0(드롭)으로 값 1(유지)을 취합니다. 확률로 p. 이를 구현하는 한 가지 쉬운 방법은 균일 분포 U[0,1]에서 먼저 샘플을 추출하는 것입니다. 그런 다음 해당 샘플이 p보다 큰 노드를 유지하고 나머지는 삭제할 수 있습니다.
In the following code, we implement a dropout_layer function that drops out the elements in the tensor input X with probability dropout, rescaling the remainder as described above: dividing the survivors by 1.0-dropout.
다음 코드에서는 텐서 입력 X의 요소를 드롭아웃 확률로 드롭아웃하는 dropout_layer 함수를 구현하고 나머지는 위에서 설명한 대로 생존자를 1.0-드롭아웃으로 나눕니다.
def dropout_layer(X, dropout):
assert 0 <= dropout <= 1
if dropout == 1: return torch.zeros_like(X)
mask = (torch.rand(X.shape) > dropout).float()
return mask * X / (1.0 - dropout)위 코드는 드롭아웃(Dropout) 레이어를 구현한 함수입니다.
드롭아웃은 신경망에서 과적합을 방지하기 위해 사용되는 정규화 기법 중 하나로, 학습 중에 일부 뉴런을 임시로 제거하여 모델의 일반화 성능을 향상시키는 역할을 합니다.
이 함수는 입력인 X와 드롭아웃 확률인 dropout을 받습니다. dropout은 0과 1 사이의 값이어야 합니다. 만약 dropout이 1이라면 모든 뉴런을 제거하고 0으로 채운 텐서를 반환합니다. 그렇지 않은 경우에는 X와 같은 크기의 마스크를 생성하여 드롭아웃을 적용합니다.
마스크는 X와 같은 크기의 텐서를 생성하고, 각 요소가 dropout보다 큰 경우에는 1로 설정하고 dropout보다 작은 경우에는 0으로 설정합니다. 이렇게 함으로써 dropout 확률에 따라 일부 뉴런이 제거되는 효과를 얻을 수 있습니다.
마스크를 X와 곱한 뒤 dropout에 대한 보정을 수행하여 드롭아웃된 결과를 반환합니다. 보정은 마스크를 dropout의 보정값인 1/(1 - dropout)으로 나누어 줌으로써 드롭아웃이 적용된 값을 보정하는 역할을 합니다.
이렇게 구현된 dropout_layer 함수는 드롭아웃이 적용된 X를 반환합니다.
We can test out the dropout_layer function on a few examples. In the following lines of code, we pass our input X through the dropout operation, with probabilities 0, 0.5, and 1, respectively.
몇 가지 예에서 dropout_layer 함수를 테스트할 수 있습니다. 다음 코드 줄에서는 각각 확률 0, 0.5 및 1로 드롭아웃 작업을 통해 입력 X를 전달합니다.
X = torch.arange(16, dtype = torch.float32).reshape((2, 8))
print('dropout_p = 0:', dropout_layer(X, 0))
print('dropout_p = 0.5:', dropout_layer(X, 0.5))
print('dropout_p = 1:', dropout_layer(X, 1))위 코드는 주어진 입력 X에 대해 dropout_layer 함수를 적용하여 드롭아웃된 결과를 출력하는 예시입니다.
입력 X는 크기가 (2, 8)인 2차원 텐서로, 각 원소는 0부터 15까지의 값으로 초기화되어 있습니다.
첫 번째 출력은 dropout_p가 0인 경우입니다. 즉, 드롭아웃 확률이 0이므로 모든 원소를 유지합니다. 따라서 출력은 입력 X와 동일한 텐서입니다.
두 번째 출력은 dropout_p가 0.5인 경우입니다. 드롭아웃 확률이 0.5이므로 각 원소가 0.5의 확률로 제거됩니다. 따라서 출력은 입력 X와 같은 크기의 텐서이지만, 일부 원소가 0으로 바뀌어 있습니다.
세 번째 출력은 dropout_p가 1인 경우입니다. 드롭아웃 확률이 1이므로 모든 원소가 제거되고 0으로 채워진 텐서가 반환됩니다.
이를 통해 드롭아웃 확률에 따라 일부 뉴런이 제거되는 효과를 확인할 수 있습니다.

5.6.2.1. Defining the Model
The model below applies dropout to the output of each hidden layer (following the activation function). We can set dropout probabilities for each layer separately. A common trend is to set a lower dropout probability closer to the input layer. We ensure that dropout is only active during training.
아래 모델은 각 숨겨진 레이어의 출력에 드롭아웃을 적용합니다(활성화 함수에 따름). 각 레이어에 대해 개별적으로 드롭아웃 확률을 설정할 수 있습니다. 일반적인 추세는 드롭아웃 확률을 입력 레이어에 더 가깝게 설정하는 것입니다. 교육 중에만 드롭아웃이 활성화되도록 합니다.
class DropoutMLPScratch(d2l.Classifier):
def __init__(self, num_outputs, num_hiddens_1, num_hiddens_2,
dropout_1, dropout_2, lr):
super().__init__()
self.save_hyperparameters()
self.lin1 = nn.LazyLinear(num_hiddens_1)
self.lin2 = nn.LazyLinear(num_hiddens_2)
self.lin3 = nn.LazyLinear(num_outputs)
self.relu = nn.ReLU()
def forward(self, X):
H1 = self.relu(self.lin1(X.reshape((X.shape[0], -1))))
if self.training:
H1 = dropout_layer(H1, self.dropout_1)
H2 = self.relu(self.lin2(H1))
if self.training:
H2 = dropout_layer(H2, self.dropout_2)
return self.lin3(H2)
위 코드는 Dropout을 적용한 MLPScratch 모델 클래스를 정의하는 예시입니다.
이 모델은 입력 X를 받아 여러 개의 선형 레이어와 ReLU 활성화 함수를 거쳐 최종 출력을 생성합니다. 중간 레이어의 출력에는 Dropout이 적용됩니다.
- self.lin1, self.lin2, self.lin3: 선형 레이어 객체로, 입력과 출력의 차원을 매개변수로 설정하여 초기화됩니다.
- self.relu: ReLU 활성화 함수 객체로, ReLU 함수를 적용하기 위해 사용됩니다.
forward 메서드에서는 다음과 같은 과정을 거쳐 입력을 처리합니다:
- 입력 X를 2차원으로 재구성합니다. 입력의 첫 번째 차원은 배치 크기를 의미합니다.
- self.lin1을 통과한 결과에 ReLU 활성화 함수를 적용하여 H1을 얻습니다. 이때, 모델이 학습 중인 경우에만 Dropout이 적용됩니다.
- self.lin2를 통과한 결과에 ReLU 활성화 함수를 적용하여 H2를 얻습니다. 마찬가지로, 모델이 학습 중인 경우에만 Dropout이 적용됩니다.
- self.lin3을 통과한 결과를 반환합니다.
이를 통해 Dropout을 적용한 다층 퍼셉트론 모델의 순전파 과정을 구현하였습니다.
5.6.2.2. Training
The following is similar to the training of MLPs described previously.
다음은 앞에서 설명한 MLP 교육과 유사합니다.
hparams = {'num_outputs':10, 'num_hiddens_1':256, 'num_hiddens_2':256,
'dropout_1':0.5, 'dropout_2':0.5, 'lr':0.1}
model = DropoutMLPScratch(**hparams)
data = d2l.FashionMNIST(batch_size=256)
trainer = d2l.Trainer(max_epochs=10)
trainer.fit(model, data)위 코드는 Dropout을 적용한 MLPScratch 모델을 생성하고 학습하는 예시입니다.
- hparams: 모델의 하이퍼파라미터를 저장한 딕셔너리입니다. 'num_outputs', 'num_hiddens_1', 'num_hiddens_2', 'dropout_1', 'dropout_2', 'lr' 키를 갖고 각각 출력 개수, 첫 번째 은닉층 크기, 두 번째 은닉층 크기, 첫 번째 Dropout 비율, 두 번째 Dropout 비율, 학습률을 값으로 갖습니다.
- model: DropoutMLPScratch 클래스의 인스턴스로, 앞서 정의한 하이퍼파라미터를 인자로 넘겨 생성됩니다.
- data: d2l.FashionMNIST를 통해 FashionMNIST 데이터셋을 로드한 결과를 저장한 변수입니다. 배치 크기는 256로 설정되어 있습니다.
- trainer: d2l.Trainer 클래스의 인스턴스로, 최대 에포크 수를 10으로 설정한 후 생성됩니다.
trainer.fit(model, data) 코드는 모델을 지정된 데이터로 학습하는 과정을 나타냅니다. Trainer 객체는 모델과 데이터를 받아서 학습 과정을 관리하고 최적화 알고리즘을 적용합니다. 이를 통해 Dropout을 적용한 MLPScratch 모델이 FashionMNIST 데이터셋으로 학습되며, 10번의 에포크 동안 훈련됩니다.

5.6.3. Concise Implementation
With high-level APIs, all we need to do is add a Dropout layer after each fully connected layer, passing in the dropout probability as the only argument to its constructor. During training, the Dropout layer will randomly drop out outputs of the previous layer (or equivalently, the inputs to the subsequent layer) according to the specified dropout probability. When not in training mode, the Dropout layer simply passes the data through during testing.
높은 수준의 API를 사용하여 우리가 해야 할 일은 각각의 완전히 연결된 레이어 뒤에 드롭아웃 레이어를 추가하고 드롭아웃 확률을 해당 생성자에 대한 유일한 인수로 전달하는 것입니다. 교육 중에 드롭아웃 레이어는 지정된 드롭아웃 확률에 따라 이전 레이어의 출력(또는 동등하게 후속 레이어의 입력)을 임의로 드롭아웃합니다. 교육 모드가 아닌 경우 Dropout 레이어는 테스트 중에 데이터를 통과시킵니다.
class DropoutMLP(d2l.Classifier):
def __init__(self, num_outputs, num_hiddens_1, num_hiddens_2,
dropout_1, dropout_2, lr):
super().__init__()
self.save_hyperparameters()
self.net = nn.Sequential(
nn.Flatten(), nn.LazyLinear(num_hiddens_1), nn.ReLU(),
nn.Dropout(dropout_1), nn.LazyLinear(num_hiddens_2), nn.ReLU(),
nn.Dropout(dropout_2), nn.LazyLinear(num_outputs))위 코드는 Dropout을 적용한 MLP 모델을 생성하는 예시입니다.
- num_outputs: 출력 개수
- num_hiddens_1: 첫 번째 은닉층의 크기
- num_hiddens_2: 두 번째 은닉층의 크기
- dropout_1: 첫 번째 Dropout 비율
- dropout_2: 두 번째 Dropout 비율
- lr: 학습률
DropoutMLP 클래스는 d2l.Classifier를 상속하고 있으며, 모델의 하이퍼파라미터를 저장합니다. self.net은 nn.Sequential로 구성되어 있으며, 각 층은 다음과 같이 순서대로 쌓입니다:
- nn.Flatten(): 입력을 1차원으로 펼치는 층
- nn.LazyLinear(num_hiddens_1): 첫 번째 은닉층
- nn.ReLU(): ReLU 활성화 함수
- nn.Dropout(dropout_1): 첫 번째 Dropout 층
- nn.LazyLinear(num_hiddens_2): 두 번째 은닉층
- nn.ReLU(): ReLU 활성화 함수
- nn.Dropout(dropout_2): 두 번째 Dropout 층
- nn.LazyLinear(num_outputs): 출력층
이를 통해 DropoutMLP 모델은 입력 데이터를 받아서 두 개의 은닉층과 Dropout 층을 거쳐 최종 출력층으로 전달하는 MLP 구조를 가지게 됩니다.
Next, we train the model.
model = DropoutMLP(**hparams)
trainer.fit(model, data)위 코드는 Dropout을 적용한 MLP 모델을 생성하고 학습하는 예시입니다.
먼저 DropoutMLP 클래스의 객체인 model을 생성합니다. **hparams는 딕셔너리 hparams의 키-값 쌍을 키워드 인자로 전달하는 방식입니다. hparams는 모델의 하이퍼파라미터를 지정한 딕셔너리입니다. 이를 통해 model은 지정된 하이퍼파라미터로 초기화된 Dropout을 적용한 MLP 모델이 됩니다.
그리고 trainer.fit(model, data)를 호출하여 모델을 주어진 데이터셋 data에 대해 학습시킵니다. Trainer 클래스는 주어진 모델과 데이터를 사용하여 학습을 수행하는 기능을 제공합니다. max_epochs=10는 최대 에포크 수를 10으로 지정한 것을 의미합니다. 즉, 모델은 주어진 데이터셋을 10번 반복하여 학습하게 됩니다.

5.6.4. Summary
Beyond controlling the number of dimensions and the size of the weight vector, dropout is yet another tool to avoid overfitting. Often they are used jointly. Note that dropout is used only during training: it replaces an activation ℎ with a random variable with expected value ℎ.
차원 수와 가중치 벡터의 크기를 제어하는 것 외에도 드롭아웃은 과적합을 방지하는 또 다른 도구입니다. 종종 그들은 공동으로 사용됩니다. 드롭아웃은 훈련 중에만 사용된다는 점에 유의하십시오. 활성화 ℎ를 예상 값 ℎ이 있는 임의 변수로 대체합니다.
5.6.5. Exercises
- What happens if you change the dropout probabilities for the first and second layers? In particular, what happens if you switch the ones for both layers? Design an experiment to answer these questions, describe your results quantitatively, and summarize the qualitative takeaways.
- Increase the number of epochs and compare the results obtained when using dropout with those when not using it.
- What is the variance of the activations in each hidden layer when dropout is and is not applied? Draw a plot to show how this quantity evolves over time for both models.
- Why is dropout not typically used at test time?
- Using the model in this section as an example, compare the effects of using dropout and weight decay. What happens when dropout and weight decay are used at the same time? Are the results additive? Are there diminished returns (or worse)? Do they cancel each other out?
- What happens if we apply dropout to the individual weights of the weight matrix rather than the activations?
- Invent another technique for injecting random noise at each layer that is different from the standard dropout technique. Can you develop a method that outperforms dropout on the Fashion-MNIST dataset (for a fixed architecture)?
'Dive into Deep Learning > D2L Multilayer Perceptrons Builder Guide' 카테고리의 다른 글
| D2L - 5.7. Predicting House Prices on Kaggle (0) | 2023.07.03 |
|---|---|
| D2L - 5.5. Generalization in Deep Learning (0) | 2023.07.03 |
| D2L - 5.4. Numerical Stability and Initialization (0) | 2023.07.02 |
| D2L - 5.3. Forward Propagation, Backward Propagation, and Computational Graphs (0) | 2023.07.02 |
| D2L - 5.2. Implementation of Multilayer Perceptrons (0) | 2023.07.01 |
| D2L - 5.1. Multilayer Perceptrons (0) | 2023.07.01 |
| D2L - 5. Multilayer Perceptrons (1) | 2023.06.30 |

