https://d2l.ai/chapter_preliminaries/linear-algebra.html
2.3. Linear Algebra — Dive into Deep Learning 1.0.3 documentation
d2l.ai
2.3. Linear Algebra
By now, we can load datasets into tensors and manipulate these tensors with basic mathematical operations. To start building sophisticated models, we will also need a few tools from linear algebra. This section offers a gentle introduction to the most essential concepts, starting from scalar arithmetic and ramping up to matrix multiplication.
이제 데이터 세트를 텐서에 로드하고 기본적인 수학 연산을 통해 이러한 텐서를 조작할 수 있습니다. 정교한 모델 구축을 시작하려면 선형 대수학의 몇 가지 도구도 필요합니다. 이 섹션에서는 스칼라 산술부터 시작하여 행렬 곱셈까지 가장 필수적인 개념을 부드럽게 소개합니다.
import torch- import torch: 이 코드는 PyTorch 라이브러리를 현재 Python 스크립트 또는 환경으로 가져옵니다. PyTorch는 딥러닝 및 텐서 연산을 위한 라이브러리로, 다양한 딥러닝 모델을 구축하고 학습시키며 텐서 관련 작업을 수행하는 데 사용됩니다.
2.3.1. Scalars
Most everyday mathematics consists of manipulating numbers one at a time. Formally, we call these values scalars. For example, the temperature in Palo Alto is a balmy 72 degrees Fahrenheit. If you wanted to convert the temperature to Celsius you would evaluate the expression c=5/9( ƒ −32), setting ƒ to 72. In this equation, the values 5, 9, and 32 are constant scalars. The variables c and ƒ in general represent unknown scalars.
대부분의 일상 수학은 한 번에 하나씩 숫자를 조작하는 것으로 구성됩니다. 공식적으로는 이러한 값을 스칼라라고 부릅니다. 예를 들어, 팔로알토(Palo Alto)의 기온은 화씨 72도입니다. 온도를 섭씨로 변환하려면 c=5/9( f −32) 표현식을 평가하고 f를 72로 설정합니다. 이 방정식에서 값 5, 9, 32는 상수 스칼라입니다. 변수 c와 f는 일반적으로 알 수 없는 스칼라를 나타냅니다.
We denote scalars by ordinary lower-cased letters (e.g., x, y, and z) and the space of all (continuous) real-valued scalars by ℝ . For expedience, we will skip past rigorous definitions of spaces: just remember that the expression x∈ ℝ is a formal way to say that x is a real-valued scalar. The symbol ∈ (pronounced “in”) denotes membership in a set. For example, x,y∈{0,1} indicates that x and y are variables that can only take values 0 or 1.
스칼라는 일반 소문자(예: x, y, z)로 표시하고 모든(연속) 실수 값 스칼라의 공간은 ℝ로 표시합니다. 편의상 공간에 대한 엄격한 정의는 생략하겠습니다. x∈ ℝ라는 표현은 x가 실수 값 스칼라임을 나타내는 형식적인 방법이라는 점만 기억하세요. 기호 ∈(“in”으로 발음)는 집합에 속한다는 것을 나타냅니다. 예를 들어, x,y∈{0,1}은 x와 y가 0 또는 1 값만 가질 수 있는 변수임을 나타냅니다.
Scalars are implemented as tensors that contain only one element. Below, we assign two scalars and perform the familiar addition, multiplication, division, and exponentiation operations.
스칼라는 하나의 요소만 포함하는 텐서로 구현됩니다. 아래에서는 두 개의 스칼라를 할당하고 익숙한 덧셈, 곱셈, 나눗셈 및 지수 연산을 수행합니다.
x = torch.tensor(3.0)
y = torch.tensor(2.0)
x + y, x * y, x / y, x**y, x-y주어진 코드는 PyTorch를 사용하여 두 개의 텐서 x와 y를 생성하고, 이를 활용하여 다양한 수학 연산을 수행하는 예제입니다. 아래는 코드의 설명입니다:
- x = torch.tensor(3.0): x라는 이름의 PyTorch 텐서를 생성하고, 값으로 3.0을 할당합니다.
- y = torch.tensor(2.0): y라는 이름의 PyTorch 텐서를 생성하고, 값으로 2.0을 할당합니다.
- x + y: x와 y의 덧셈을 수행합니다. 결과로 새로운 텐서가 생성되며, 이 텐서의 값은 3.0 + 2.0으로 5.0이 됩니다.
- x * y: x와 y의 곱셈을 수행합니다. 결과로 새로운 텐서가 생성되며, 이 텐서의 값은 3.0 * 2.0으로 6.0이 됩니다.
- x / y: x를 y로 나눗셈을 수행합니다. 결과로 새로운 텐서가 생성되며, 이 텐서의 값은 3.0 / 2.0으로 1.5가 됩니다.
- x**y: x를 y 제곱 연산을 수행합니다. 결과로 새로운 텐서가 생성되며, 이 텐서의 값은 3.0의 2.0 제곱으로 9.0이 됩니다.
- x - y: x와 y의 뺄셈을 수행합니다. 결과로 새로운 텐서가 생성되며, 이 텐서의 값은 3.0 - 2.0으로 1.0이 됩니다.
코드를 실행하면 각 연산의 결과가 출력됩니다. PyTorch를 사용하면 텐서를 활용하여 다양한 수학적 연산을 수행할 수 있으며, 딥러닝 모델의 학습과 예측 등에 활용됩니다.
(tensor(5.), tensor(6.), tensor(1.5000), tensor(9.), tensor(1.))
2.3.2. Vectors
For current purposes, you can think of a vector as a fixed-length array of scalars. As with their code counterparts, we call these scalars the elements of the vector (synonyms include entries and components). When vectors represent examples from real-world datasets, their values hold some real-world significance. For example, if we were training a model to predict the risk of a loan defaulting, we might associate each applicant with a vector whose components correspond to quantities like their income, length of employment, or number of previous defaults. If we were studying the risk of heart attack, each vector might represent a patient and its components might correspond to their most recent vital signs, cholesterol levels, minutes of exercise per day, etc. We denote vectors by bold lowercase letters, (e.g., x, y, and z).
현재 목적상 벡터를 스칼라의 고정 길이 배열로 생각할 수 있습니다. 해당 코드와 마찬가지로 이러한 스칼라를 벡터의 요소라고 부릅니다(동의어에는 항목과 구성 요소가 포함됨). 벡터가 실제 데이터 세트의 예를 나타내는 경우 해당 값은 실제 의미를 갖습니다. 예를 들어, 대출 불이행 위험을 예측하기 위해 모델을 훈련하는 경우 각 지원자를 소득, 고용 기간 또는 이전 불이행 횟수와 같은 수량에 해당하는 구성요소가 있는 벡터와 연결할 수 있습니다. 심장 마비의 위험을 연구하는 경우 각 벡터는 환자를 나타낼 수 있으며 그 구성 요소는 가장 최근의 활력 징후, 콜레스테롤 수치, 일일 운동 시간(분) 등에 해당할 수 있습니다. 벡터는 굵은 소문자로 표시됩니다(예: x, y, z).
Vectors are implemented as 1 st-order tensors. In general, such tensors can have arbitrary lengths, subject to memory limitations. Caution: in Python, as in most programming languages, vector indices start at 0, also known as zero-based indexing, whereas in linear algebra subscripts begin at 1 (one-based indexing).
벡터는 1차 텐서로 구현됩니다. 일반적으로 이러한 텐서는 메모리 제한에 따라 임의의 길이를 가질 수 있습니다. 주의: Python에서는 대부분의 프로그래밍 언어와 마찬가지로 벡터 인덱스가 0부터 시작합니다(0부터 시작하는 인덱싱이라고도 함). 반면 선형 대수학 첨자는 1(1부터 시작하는 인덱싱)에서 시작합니다.
x = torch.arange(3)
x주어진 코드는 PyTorch를 사용하여 텐서 x를 생성하는 예제입니다. 아래는 코드의 설명입니다:
- x = torch.arange(3): torch.arange() 함수를 사용하여 x라는 이름의 PyTorch 텐서를 생성합니다. torch.arange() 함수는 주어진 범위 내의 정수를 순서대로 생성하는 함수로, 여기서는 0부터 2까지의 정수를 생성하게 됩니다. 따라서 x는 [0, 1, 2]라는 값을 가지는 1차원 텐서가 됩니다.
- x: 텐서 x를 출력합니다. 이 코드는 텐서 x의 내용을 화면에 출력하여 확인할 수 있습니다.
결과적으로, 코드를 실행하면 x라는 이름의 PyTorch 텐서가 생성되며, 그 값은 [0, 1, 2]인 1차원 배열로 출력됩니다. PyTorch의 텐서는 수학 및 딥러닝 연산에 사용되며, 다양한 데이터 처리 및 모델 학습 작업에 활용됩니다.
tensor([0, 1, 2])We can refer to an element of a vector by using a subscript. For example, x2 denotes the second element of x. Since x2 is a scalar, we do not bold it. By default, we visualize vectors by stacking their elements vertically.
아래 첨자를 사용하여 벡터의 요소를 참조할 수 있습니다. 예를 들어 x2는 x의 두 번째 요소를 나타냅니다. x2는 스칼라이므로 굵게 표시하지 않습니다. 기본적으로 벡터의 요소를 수직으로 쌓아서 벡터를 시각화합니다.

Here x1,…,xn are elements of the vector. Later on, we will distinguish between such column vectors and row vectors whose elements are stacked horizontally. Recall that we access a tensor’s elements via indexing.
여기서 x1,…,xn은 벡터의 요소입니다. 나중에 이러한 열 벡터와 요소가 가로로 쌓인 행 벡터를 구분할 것입니다. 인덱싱을 통해 텐서의 요소에 액세스한다는 점을 기억하세요.
x[2]주어진 코드는 PyTorch 텐서 x에서 특정 인덱스에 해당하는 값을 추출하는 예제입니다. 아래는 코드의 설명입니다:
- x[2]: 이 코드는 PyTorch 텐서 x에서 인덱스 2에 해당하는 값을 추출하는 작업을 수행합니다. 텐서 x는 0부터 시작하는 인덱스를 가지며, 2번 인덱스는 세 번째 원소를 나타냅니다.
예를 들어, 만약 x가 [0, 1, 2]라는 값을 가진 1차원 텐서라면, x[2]는 2번 인덱스에 해당하는 값인 2를 반환합니다.
이 코드를 실행하면 x 텐서에서 해당 인덱스의 값을 추출하여 반환합니다. 결과적으로, x[2]는 x 텐서의 세 번째 원소에 해당하는 값을 반환합니다.
tensor(2)
To indicate that a vector contains n elements, we write x∈ ℝn. Formally, we call n the dimensionality of the vector. In code, this corresponds to the tensor’s length, accessible via Python’s built-in len function.
벡터에 n개의 요소가 포함되어 있음을 나타내기 위해 x∈ ℝn이라고 씁니다. 공식적으로 n을 벡터의 차원이라고 부릅니다. 코드에서 이는 Python의 내장 len 함수를 통해 액세스할 수 있는 텐서의 길이에 해당합니다.
len(x)주어진 코드는 PyTorch 텐서 x의 길이(원소의 개수)를 반환하는 예제입니다. 아래는 코드의 설명입니다:
- len(x): 이 코드는 PyTorch 텐서 x의 길이를 반환합니다. 텐서의 길이는 해당 텐서에 포함된 원소의 개수를 나타냅니다.
예를 들어, x가 [0, 1, 2]라는 값을 가진 1차원 텐서라면, len(x)는 3을 반환합니다. 즉, 이 텐서에는 3개의 원소가 포함되어 있습니다.
이 코드를 실행하면 x 텐서의 길이가 반환됩니다. 결과적으로, len(x)는 x 텐서에 포함된 원소의 개수를 나타내는 정수를 반환합니다.
3
We can also access the length via the shape attribute. The shape is a tuple that indicates a tensor’s length along each axis. Tensors with just one axis have shapes with just one element.
Shape 속성을 통해 길이에 접근할 수도 있습니다. 모양은 각 축을 따라 텐서의 길이를 나타내는 튜플입니다. 축이 하나뿐인 텐서는 요소가 하나만 있는 모양을 갖습니다.
x.shape주어진 코드는 PyTorch 텐서 x의 모양(shape)을 반환하는 예제입니다. 아래는 코드의 설명입니다:
- x.shape: 이 코드는 PyTorch 텐서 x의 모양(shape)을 반환합니다. 모양은 텐서가 어떻게 구성되어 있는지를 나타내며, 차원과 각 차원의 크기를 포함합니다.
예를 들어, 만약 x가 2차원 텐서이고 모양이 (3, 4)라면, x.shape는 (3, 4)를 반환합니다. 이는 3개의 행과 4개의 열로 이루어진 2차원 텐서임을 나타냅니다.
이 코드를 실행하면 x 텐서의 모양이 반환됩니다. 결과적으로, x.shape는 텐서의 차원과 각 차원의 크기를 나타내는 튜플을 반환합니다.
torch.Size([3])Oftentimes, the word “dimension” gets overloaded to mean both the number of axes and the length along a particular axis. To avoid this confusion, we use order to refer to the number of axes and dimensionality exclusively to refer to the number of components.
종종 " dimension 차원"이라는 단어는 축 수와 특정 축의 길이를 모두 의미하는 것으로 오버로드됩니다. 이러한 혼란을 피하기 위해 우리는 축 수를 참조하기 위해 순서 order 를 사용하고 구성 요소 수를 참조하기 위해 차원 dimensionality 을 독점적으로 사용합니다.
2.3.3. Matrices
Just as scalars are 0 th-order tensors and vectors are 1 st-order tensors, matrices are 2 nd-order tensors. We denote matrices by bold capital letters (e.g., X, Y, and Z), and represent them in code by tensors with two axes. The expression A∈ ℝ m×n indicates that a matrix A contains m×n real-valued scalars, arranged as m rows and n columns. When m=n, we say that a matrix is square. Visually, we can illustrate any matrix as a table. To refer to an individual element, we subscript both the row and column indices, e.g., aij is the value that belongs to A’s i th row and j th column:
스칼라가 0차 텐서이고 벡터가 1차 텐서인 것처럼 행렬은 2차 텐서입니다. 행렬은 굵은 대문자(예: X, Y, Z)로 표시하고 두 개의 축이 있는 텐서로 코드로 표시합니다. A∈ ℝm×n 표현식은 행렬 A가 m행과 n열로 배열된 m×n 실수 값 스칼라를 포함함을 나타냅니다. m=n일 때, 행렬은 square 이라고 말합니다. 시각적으로 모든 행렬을 테이블로 설명할 수 있습니다. 개별 요소를 참조하기 위해 행과 열 인덱스를 모두 첨자로 표시합니다. 예를 들어 aij는 A의 i 번째 행과 j 번째 열에 속하는 값입니다.

In code, we represent a matrix A∈ ℝ m×n by a 2nd-order tensor with shape (m, n). We can convert any appropriately sized m×n tensor into an m×n matrix by passing the desired shape to reshape:
코드에서는 행렬 A∈ ℝm×n을 모양이 (m, n)인 2차 텐서로 표현합니다. 원하는 모양을 전달하여 적절한 크기의 m×n 텐서를 m×n 행렬로 변환할 수 있습니다.
A = torch.arange(6).reshape(3, 2)
A주어진 코드는 PyTorch를 사용하여 텐서 A를 생성하고, 그 모양을 변경하는 작업을 수행하는 예제입니다. 아래는 코드의 설명입니다:
- A = torch.arange(6): torch.arange() 함수를 사용하여 0부터 5까지의 정수로 이루어진 1차원 텐서 A를 생성합니다. 이 텐서는 [0, 1, 2, 3, 4, 5]와 같은 값을 가지게 됩니다.
- .reshape(3, 2): 생성한 텐서 A의 모양을 변경합니다. .reshape() 메서드를 사용하여 텐서의 모양을 변경할 수 있으며, 여기서는 (3, 2) 모양으로 변경합니다. 따라서 텐서 A는 3개의 행과 2개의 열로 이루어진 2차원 텐서가 됩니다.
- A: 변경된 텐서 A를 출력합니다. 이 코드는 변경된 모양의 텐서 A를 확인할 수 있도록 출력합니다.
결과적으로, 코드를 실행하면 0부터 5까지의 값을 가진 1차원 텐서 A가 생성되고, 그 후 (3, 2) 모양으로 변경된 텐서 A가 출력됩니다. 이처럼 PyTorch를 사용하면 텐서의 모양을 변경하여 데이터를 원하는 형태로 조작할 수 있습니다.
tensor([[0, 1],
[2, 3],
[4, 5]])
Sometimes we want to flip the axes. When we exchange a matrix’s rows and columns, the result is called its transpose. Formally, we signify a matrix A’s transpose by A⊤ and if B=A⊤, then bij=aji for all i and j. Thus, the transpose of an m×n matrix is an n×m matrix:
때로는 축을 뒤집고 싶을 때도 있습니다. 행렬의 행과 열을 교환할 때의 결과를 전치 transpose 라고 합니다. 공식적으로, 행렬 A의 전치를 A⊤로 표시하고 B=A⊤이면 모든 i와 j에 대해 bij=aji입니다. 따라서 m×n 행렬의 전치는 n×m 행렬입니다.
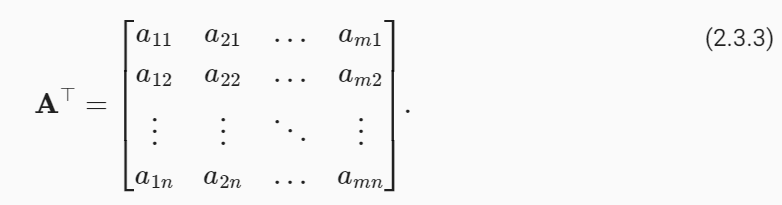
In code, we can access any matrix’s transpose as follows:
코드에서는 다음과 같이 모든 행렬의 전치에 액세스할 수 있습니다.
A.Ttensor([[0, 2, 4],
[1, 3, 5]])주어진 코드 A.T는 PyTorch 텐서 A의 전치(transpose)를 반환하는 작업을 나타냅니다. 아래는 코드의 설명입니다:
- A.T: 이 코드는 텐서 A의 전치(transpose)를 반환합니다. 전치란 원본 행렬 또는 텐서의 행과 열을 바꾼 것을 의미합니다. 즉, 텐서 A의 행은 열로, 열은 행으로 바뀝니다.
예를 들어, 만약 텐서 A가 다음과 같다면:
A = torch.tensor([[0, 1],
[2, 3],
[4, 5]])
A.T는 다음과 같이 전치된 텐서를 반환합니다:
tensor([[0, 2, 4],
[1, 3, 5]])
결과적으로, A.T 코드를 실행하면 텐서 A의 전치된 형태인 새로운 텐서가 반환됩니다. 이렇게 하면 원본 텐서의 행과 열이 바뀐 모양의 텐서를 얻을 수 있습니다.
Symmetric matrices are the subset of square matrices that are equal to their own transposes: A=A⊤. The following matrix is symmetric:
대칭 행렬은 자체 전치와 동일한 정사각형 행렬의 하위 집합입니다(A=A⊤). 다음 행렬은 대칭입니다.
A = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]])
A == A.T주어진 코드는 PyTorch 텐서 A와 그 전치(A.T) 간의 요소별 비교를 수행하고 결과를 반환하는 예제입니다. 아래는 코드의 설명입니다:
- A = torch.tensor([[1, 2, 3], [2, 0, 4], [3, 4, 5]]): 텐서 A를 생성합니다. 이 텐서는 3x3 크기의 2차원 배열을 나타내며, 각 요소의 값은 주어진 값으로 초기화됩니다.
- A.T: 텐서 A의 전치(transpose)를 계산합니다. 이렇게 하면 원본 텐서의 행과 열이 바뀐 형태의 텐서가 생성됩니다.
- A == A.T: 원본 텐서 A와 그 전치 텐서 A.T 간의 요소별(원소별) 비교를 수행합니다. 두 텐서의 같은 위치에 있는 요소끼리 비교하며, 결과는 두 텐서가 동일한 요소를 가지면 True로, 다른 경우에는 False로 나타납니다.
결과적으로, A == A.T 코드를 실행하면 A와 A의 전치 텐서 A.T 간의 요소별 비교 결과를 반환합니다. 이 코드의 결과는 A와 A.T가 대칭 행렬인 경우에만 모든 요소가 True가 됩니다. 다시 말해, A가 대칭 행렬이라면 A == A.T는 모든 요소가 True를 반환할 것입니다.
tensor([[True, True, True],
[True, True, True],
[True, True, True]])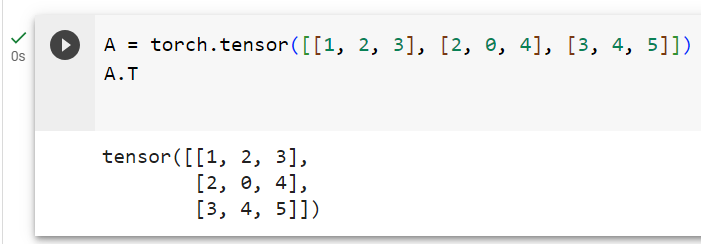
Matrices are useful for representing datasets. Typically, rows correspond to individual records and columns correspond to distinct attributes.
행렬은 데이터 세트를 나타내는 데 유용합니다. 일반적으로 행은 개별 레코드에 해당하고 열은 고유한 속성에 해당합니다.
2.3.4. Tensors
While you can go far in your machine learning journey with only scalars, vectors, and matrices, eventually you may need to work with higher-order tensors. Tensors give us a generic way of describing extensions to nth-order arrays. We call software objects of the tensor class “tensors” precisely because they too can have arbitrary numbers of axes. While it may be confusing to use the word tensor for both the mathematical object and its realization in code, our meaning should usually be clear from context. We denote general tensors by capital letters with a special font face (e.g., X, Y, and Z) and their indexing mechanism (e.g., xijk and [X]1,2i−1,3) follows naturally from that of matrices.
스칼라, 벡터 및 행렬만으로 기계 학습 여정을 멀리할 수 있지만 결국에는 고차 텐서를 사용하여 작업해야 할 수도 있습니다. 텐서는 n차 배열에 대한 확장을 설명하는 일반적인 방법을 제공합니다. 우리는 텐서 클래스의 소프트웨어 객체를 "텐서"라고 부릅니다. 왜냐하면 그들 역시 임의의 수의 축을 가질 수 있기 때문입니다. 수학적 객체와 코드에서의 구현 모두에 대해 텐서라는 단어를 사용하는 것이 혼란스러울 수 있지만 일반적으로 의미는 문맥에서 명확해야 합니다. 일반 텐서를 특수 글꼴(예: X, Y, Z)이 있는 대문자로 표시하며 해당 인덱싱 메커니즘(예: xijk 및 [X]1,2i−1,3)은 자연스럽게 행렬의 인덱싱 메커니즘을 따릅니다.
Tensors will become more important when we start working with images. Each image arrives as a 3rd-order tensor with axes corresponding to the height, width, and channel. At each spatial location, the intensities of each color (red, green, and blue) are stacked along the channel. Furthermore, a collection of images is represented in code by a 4th-order tensor, where distinct images are indexed along the first axis. Higher-order tensors are constructed, as were vectors and matrices, by growing the number of shape components.
이미지 작업을 시작하면 Tensor가 더욱 중요해집니다. 각 이미지는 높이, 너비 및 채널에 해당하는 축이 있는 3차 텐서로 도착합니다. 각 공간 위치에서 각 색상(빨간색, 녹색, 파란색)의 강도가 채널을 따라 누적됩니다. 또한, 이미지 모음은 코드에서 4차 텐서로 표현되며, 여기서 개별 이미지는 첫 번째 축을 따라 인덱싱됩니다. 고차 텐서는 벡터 및 행렬과 마찬가지로 모양 구성 요소의 수를 늘려 구성됩니다.
torch.arange(24).reshape(2, 3, 4)주어진 코드는 PyTorch를 사용하여 2x3x4 크기의 3차원 텐서를 생성하는 작업을 나타냅니다. 아래는 코드의 설명입니다:
- torch.arange(24): 이 코드는 0부터 23까지의 정수를 포함하는 1차원 텐서를 생성합니다. torch.arange() 함수는 주어진 범위 내의 정수를 생성하는 함수입니다.
- .reshape(2, 3, 4): 앞서 생성한 1차원 텐서를 2x3x4 크기의 다차원 텐서로 형태를 변경합니다. .reshape() 메서드를 사용하여 텐서의 모양을 변경할 수 있으며, 여기서는 (2, 3, 4) 모양으로 변경합니다. 따라서 이제 텐서는 3차원 배열로 표현되며, 크기는 2개의 "깊이" (depth), 각 깊이당 3개의 "행" (rows), 그리고 각 행당 4개의 "열" (columns)로 구성됩니다.
결과적으로, torch.arange(24).reshape(2, 3, 4) 코드를 실행하면 2x3x4 크기의 3차원 텐서가 생성됩니다. 이 텐서는 다양한 데이터를 저장하거나 다차원 배열 연산을 수행하는 데 사용될 수 있습니다.
tensor([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
2.3.5. Basic Properties of Tensor Arithmetic
Scalars, vectors, matrices, and higher-order tensors all have some handy properties. For example, elementwise operations produce outputs that have the same shape as their operands.
스칼라, 벡터, 행렬 및 고차 텐서는 모두 몇 가지 편리한 속성을 가지고 있습니다. 예를 들어 요소별 연산은 피연산자와 모양이 동일한 출력을 생성합니다.
A = torch.arange(6, dtype=torch.float32).reshape(2, 3)
B = A.clone() # Assign a copy of A to B by allocating new memory
A, A + B(tensor([[0., 1., 2.],
[3., 4., 5.]]),
tensor([[ 0., 2., 4.],
[ 6., 8., 10.]]))
주어진 코드는 PyTorch를 사용하여 두 개의 텐서 A와 B를 생성하고, 이를 활용하여 텐서 간의 덧셈 연산을 수행하는 작업을 나타냅니다. 아래는 코드의 설명입니다:
- A = torch.arange(6, dtype=torch.float32).reshape(2, 3): 먼저, 텐서 A를 생성합니다. torch.arange() 함수는 0부터 시작하여 5까지의 값을 가지는 1차원 텐서를 생성하고, 이를 .reshape(2, 3) 메서드를 사용하여 2x3 크기의 2차원 텐서로 형태를 변경합니다. 결과적으로 A는 다음과 같이 표현됩니다:
tensor([[0., 1., 2.],
[3., 4., 5.]])- B = A.clone(): 다음으로, 텐서 B를 생성합니다. 여기서 A.clone()을 사용하여 텐서 A의 복사본을 만듭니다. 이 때, 새로운 메모리를 할당하여 A와 동일한 값을 가지는 B를 생성합니다. 이로써 A와 B는 동일한 값을 가지지만 서로 다른 메모리 공간을 사용하게 됩니다.
- A, A + B: 텐서 A와 텐서 B를 출력합니다. 그리고 A + B를 사용하여 두 텐서의 요소별 덧셈 연산을 수행한 결과를 출력합니다. 덧셈 연산은 같은 위치에 있는 요소끼리 더해지며, 결과는 다음과 같이 표시됩니다:
(tensor([[0., 1., 2.],
[3., 4., 5.]]),
tensor([[ 0., 2., 4.],
[ 6., 8., 10.]]))결과적으로, 코드를 실행하면 두 개의 텐서 A와 B가 생성되고, 이를 사용하여 요소별 덧셈 연산이 수행되어 두 개의 텐서가 반환됩니다. 이렇게 PyTorch를 사용하면 텐서 연산을 쉽게 수행하고, 복사본을 만들어 원본 데이터를 보존할 수 있습니다.
The elementwise product of two matrices is called their Hadamard product (denoted ⊙). We can spell out the entries of the Hadamard product of two matrices A,B∈ ℝ m×n:
두 행렬의 요소별 곱을 하다마드 곱(Hadamard product)이라고 합니다(기호 ⊙). 두 행렬 A,B∈ ℝ m×n의 Hadamard 곱의 항목을 spell out 할 수 있습니다.
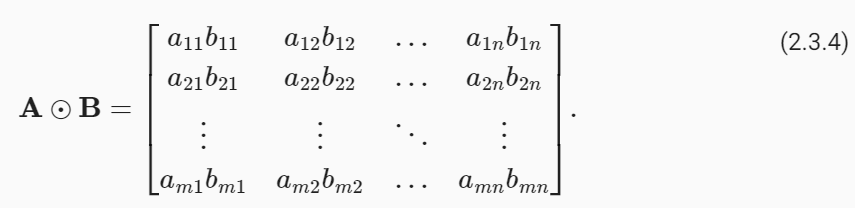
A * Btensor([[ 0., 1., 4.],
[ 9., 16., 25.]])주어진 코드 A * B는 PyTorch 텐서 A와 B 간의 요소별 곱셈 연산을 나타냅니다. 아래는 코드의 설명입니다:
- A * B: 이 코드는 텐서 A와 B 간의 요소별 곱셈을 수행합니다. 요소별 곱셈은 두 텐서의 같은 위치에 있는 요소끼리 곱셈을 수행하며, 결과는 새로운 텐서로 반환됩니다.
예를 들어, A와 B가 다음과 같다면:
A = torch.tensor([[0., 1., 2.],
[3., 4., 5.]])
B = torch.tensor([[1., 2., 3.],
[4., 5., 6.]])
A * B는 다음과 같이 요소별로 곱셈이 수행된 결과를 반환합니다:
tensor([[ 0., 2., 6.],
[12., 20., 30.]])결과적으로, A * B 코드를 실행하면 두 개의 텐서 A와 B 간의 요소별 곱셈 연산이 수행되어 새로운 텐서가 반환됩니다. 이렇게 하면 각 요소가 서로 곱해진 결과가 나타납니다. PyTorch를 사용하면 다양한 요소별 연산을 쉽게 수행할 수 있으며, 이를 활용하여 수학적 계산을 수행할 수 있습니다.
Hadamard product (Hadamard 곱)이란?
The Hadamard product, also known as the element-wise product or entrywise product, is a mathematical operation that involves multiplying each corresponding element of two matrices or vectors together.
Hadamard 곱(또는 요소별 곱셈 또는 항별 곱셈)은 두 행렬 또는 벡터의 각 해당 요소를 서로 곱하는 수학적 연산입니다.
Specifically, for two matrices A and B of the same shape (i.e., they have the same number of rows and columns), the Hadamard product C is calculated as follows:
구체적으로, 동일한 모양을 가진 두 행렬 A와 B에 대해 Hadamard 곱 C는 다음과 같이 계산됩니다:
C[i][j] = A[i][j] * B[i][j] for all valid indices i and j.
In other words, each element in the resulting matrix C is obtained by multiplying the corresponding elements of A and B. The Hadamard product differs from the more conventional matrix multiplication (dot product) in which you perform element-wise multiplication and then sum the results.
다시 말해, 결과 행렬 C의 각 요소는 A와 B의 해당 요소를 곱하여 얻어집니다. Hadamard 곱은 요소별 곱셈을 수행하고 결과를 합산하는 일반적인 행렬 곱셈과는 다릅니다.
The Hadamard product is often denoted by a circle with a dot inside it (∘) or by simply using the multiplication symbol (*), without any special operation notation.
Hadamard 곱은 두 행렬 또는 벡터의 각 요소를 독립적으로 처리하려는 경우 요소 간의 관계를 보존하면서 수행할 때 특히 유용합니다. Hadamard 곱은 일반적으로 점(∘)이 내부에 있는 원으로 표시되거나 간단히 곱셈 기호(*)를 사용하여 나타납니다.
The Hadamard product is used in various mathematical and scientific contexts, including linear algebra, signal processing, and statistics. It's particularly useful in cases where you want to perform operations on individual components of matrices or vectors independently, preserving their element-wise relationships.
Hadamard 곱은 선형 대수, 신호 처리 및 통계를 포함한 다양한 수학적 및 과학적 맥락에서 사용됩니다. 이 연산은 행렬이나 벡터의 개별 구성 요소에 대한 연산을 독립적으로 수행하고 요소 간의 관계를 보존할 때 특히 유용합니다.
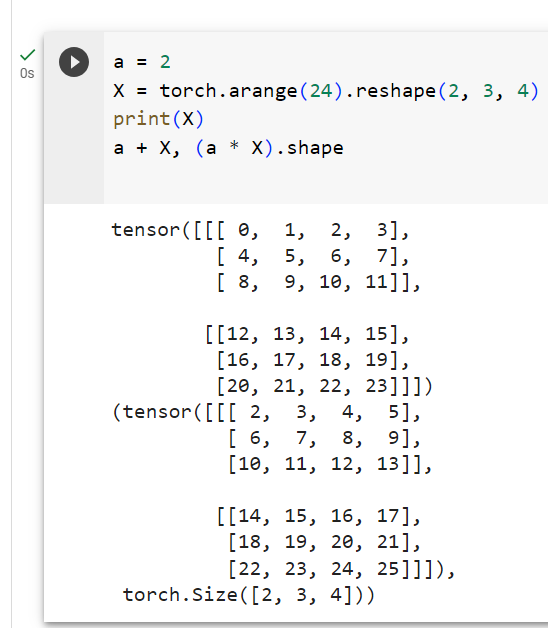
Adding or multiplying a scalar and a tensor produces a result with the same shape as the original tensor. Here, each element of the tensor is added to (or multiplied by) the scalar.
스칼라와 텐서를 더하거나 곱하면 원래 텐서와 모양이 같은 결과가 생성됩니다. 여기서 텐서의 각 요소는 스칼라에 추가되거나 곱해집니다.
a = 2
X = torch.arange(24).reshape(2, 3, 4)
a + X, (a * X).shape(tensor([[[ 2, 3, 4, 5],
[ 6, 7, 8, 9],
[10, 11, 12, 13]],
[[14, 15, 16, 17],
[18, 19, 20, 21],
[22, 23, 24, 25]]]),
torch.Size([2, 3, 4]))
주어진 코드는 PyTorch를 사용하여 스칼라 값 a와 3차원 텐서 X 간의 덧셈 연산과 곱셈 연산을 수행하는 작업을 나타냅니다. 아래는 코드의 설명입니다:
- a = 2: 변수 a에 숫자 2를 할당합니다. 이 값은 스칼라(하나의 숫자)를 나타냅니다.
- X = torch.arange(24).reshape(2, 3, 4): 0부터 23까지의 정수로 이루어진 1차원 텐서를 생성한 후, .reshape(2, 3, 4) 메서드를 사용하여 이를 2x3x4 크기의 3차원 텐서로 형태를 변경합니다. 결과적으로 X는 3차원 배열로 표현되며, 크기는 2개의 "깊이" (depth), 각 깊이당 3개의 "행" (rows), 그리고 각 행당 4개의 "열" (columns)로 구성됩니다.
- a + X: 스칼라 값 a와 3차원 텐서 X 간의 요소별 덧셈 연산을 수행합니다. 스칼라 값 a가 X의 각 요소에 더해지며, 결과는 X와 동일한 크기의 텐서로 반환됩니다.
- (a * X).shape: 스칼라 값 a와 3차원 텐서 X 간의 요소별 곱셈 연산을 수행합니다. 결과로 나오는 텐서의 모양(shape)을 확인합니다. .shape 속성은 텐서의 모양을 반환합니다.
결과적으로, 코드를 실행하면 두 개의 결과가 반환됩니다:
- 첫 번째 결과는 a가 X의 각 요소에 더해져서 생성된 텐서입니다. 이 텐서는 X와 동일한 크기를 가지며, 각 요소는 a와 X의 해당 위치 요소를 더한 값입니다.
- 두 번째 결과는 a가 X의 각 요소에 곱해진 결과인 텐서의 모양(shape)입니다. 이 경우, 곱셈 연산은 모양(shape)을 변경하지 않으므로 (2, 3, 4)와 같은 모양을 가진 원래 X와 동일한 모양을 반환합니다.
이 코드를 통해 PyTorch에서 스칼라와 텐서 간의 연산을 어떻게 수행하는지를 이해할 수 있습니다.
2.3.6. Reduction
Often, we wish to calculate the sum of a tensor’s elements. To express the sum of the elements in a vector x of length n, we write ∑n i=1 xi. There is a simple function for it:
종종 우리는 텐서 요소의 합을 계산하고 싶습니다. 길이 n의 벡터 x에 있는 요소의 합을 표현하기 위해 ∑n i=1 xi라고 씁니다. 이를 위한 간단한 기능이 있습니다:
x = torch.arange(3, dtype=torch.float32)
x, x.sum()주어진 코드는 PyTorch를 사용하여 1차원 텐서 x를 생성하고, 그 텐서의 합계를 계산하는 작업을 나타냅니다. 아래는 코드의 설명입니다:
- x = torch.arange(3, dtype=torch.float32): torch.arange() 함수를 사용하여 0부터 2까지의 정수로 이루어진 1차원 텐서 x를 생성합니다. dtype=torch.float32를 사용하여 텐서의 데이터 타입을 부동소수점(float32)으로 설정합니다.
- x: 생성한 텐서 x를 출력합니다. 이 코드는 텐서 x를 확인하기 위해 화면에 출력합니다.
- x.sum(): 텐서 x의 합계를 계산합니다. .sum() 메서드는 텐서의 모든 요소의 합을 반환합니다. 여기서는 x의 요소가 [0.0, 1.0, 2.0]이므로 합계는 0.0 + 1.0 + 2.0으로 3.0이 됩니다.
결과적으로, 코드를 실행하면 텐서 x가 생성되고, 이 텐서의 내용이 출력됩니다. 또한 x.sum()을 호출하여 텐서 x의 합계가 계산되고 출력됩니다. 이 코드는 PyTorch를 사용하여 텐서를 생성하고 기본적인 연산을 수행하는 예제를 보여줍니다.
(tensor([0., 1., 2.]), tensor(3.))
To express sums over the elements of tensors of arbitrary shape, we simply sum over all its axes. For example, the sum of the elements of an m×n matrix A could be written ∑m i=1∑n j=1 aij.
임의 형태의 텐서 요소에 대한 합을 표현하려면 단순히 모든 축에 대한 합을 구하면 됩니다. 예를 들어, m×n 행렬 A의 요소들의 합은 ∑m i=1 ∑n j=1 aij로 쓸 수 있습니다.
A.shape, A.sum()(torch.Size([2, 3]), tensor(15.))주어진 코드는 PyTorch 텐서 A의 모양(shape)과 텐서 내의 모든 요소의 합계를 계산하는 작업을 나타냅니다. 아래는 코드의 설명입니다:
- A.shape: 텐서 A의 모양(shape)을 확인하는 작업입니다. .shape 속성을 사용하면 텐서의 차원과 각 차원의 크기를 나타내는 튜플이 반환됩니다.
- A.sum(): 텐서 A의 모든 요소의 합계를 계산하는 작업입니다. .sum() 메서드를 사용하면 텐서 내의 모든 요소를 합한 결과가 반환됩니다.
결과적으로, 코드를 실행하면 두 가지 결과가 반환됩니다:
- 첫 번째 결과는 텐서 A의 모양(shape)을 나타내는 튜플입니다. 이 튜플은 텐서의 차원과 각 차원의 크기를 포함하고 있습니다. 예를 들어, (2, 3, 4)와 같은 튜플은 3차원 텐서이며, 첫 번째 차원은 2, 두 번째 차원은 3, 세 번째 차원은 4의 크기를 가집니다.
- 두 번째 결과는 텐서 A 내의 모든 요소의 합계를 나타내는 값입니다. 이 값은 텐서 내의 모든 요소를 합한 결과이므로, A의 모든 요소를 합친 총합이 됩니다.
이 코드는 텐서의 모양과 요소의 합을 확인하는 데 유용하며, 데이터 분석 및 딥러닝 모델 학습 중에 자주 사용됩니다.

By default, invoking the sum function reduces a tensor along all of its axes, eventually producing a scalar. Our libraries also allow us to specify the axes along which the tensor should be reduced. To sum over all elements along the rows (axis 0), we specify axis=0 in sum. Since the input matrix reduces along axis 0 to generate the output vector, this axis is missing from the shape of the output.
기본적으로 sum 함수를 호출하면 모든 축을 따라 텐서가 줄어들고 결국 스칼라가 생성됩니다. 우리 라이브러리를 사용하면 텐서가 감소되어야 하는 축을 지정할 수도 있습니다. 행(축 0)을 따라 모든 요소를 합산하려면 합산에 axis=0을 지정합니다. 입력 행렬은 출력 벡터를 생성하기 위해 축 0을 따라 감소하므로 이 축은 출력의 모양에서 누락됩니다.
A.shape, A.sum(axis=0).shape주어진 코드는 PyTorch 텐서 A의 모양(shape)과 axis=0를 사용하여 첫 번째 차원(열)을 따라 합산한 결과의 모양을 확인하는 작업을 나타냅니다. 아래는 코드의 설명입니다:
- A.shape: 텐서 A의 모양(shape)을 확인하는 작업입니다. .shape 속성을 사용하면 텐서의 차원과 각 차원의 크기를 나타내는 튜플이 반환됩니다.
- A.sum(axis=0): 텐서 A의 첫 번째 차원(열)을 따라 합산한 결과를 계산합니다. axis 매개변수를 사용하여 어떤 차원을 따라 합산할지 지정할 수 있으며, 여기서는 axis=0을 사용하여 첫 번째 차원을 따라 합산합니다.
- A.sum(axis=0).shape: 합산된 결과 텐서의 모양(shape)을 확인하는 작업입니다. .shape 속성을 사용하여 모양을 확인합니다.
결과적으로, 코드를 실행하면 두 가지 결과가 반환됩니다:
- 첫 번째 결과는 원래 텐서 A의 모양(shape)을 나타내는 튜플입니다.
- 두 번째 결과는 첫 번째 차원(열)을 따라 합산한 결과 텐서의 모양(shape)을 나타내는 튜플입니다. 이 결과 텐서는 첫 번째 차원이 합산되었기 때문에 원래 텐서보다 한 차원이 줄어듭니다.
이 코드를 통해 PyTorch를 사용하여 텐서의 차원 및 차원 간의 연산을 조작하고 모양(shape)을 확인하는 방법을 이해할 수 있습니다.
(torch.Size([2, 3]), torch.Size([3]))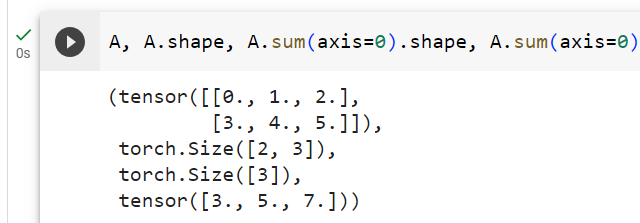
Specifying axis=1 will reduce the column dimension (axis 1) by summing up elements of all the columns.
axis=1을 지정하면 모든 열의 요소를 합산하여 열 차원(축 1)이 줄어듭니다.
A.shape, A.sum(axis=1).shape주어진 코드는 PyTorch 텐서 A의 모양(shape)과 axis=1을 사용하여 두 번째 차원(행)을 따라 합산한 결과의 모양을 확인하는 작업을 나타냅니다. 아래는 코드의 설명입니다:
- A.shape: 텐서 A의 모얥(shape)을 확인하는 작업입니다. .shape 속성을 사용하면 텐서의 차원과 각 차원의 크기를 나타내는 튜플이 반환됩니다.
- A.sum(axis=1): 텐서 A의 두 번째 차원(행)을 따라 합산한 결과를 계산합니다. axis 매개변수를 사용하여 어떤 차원을 따라 합산할지 지정할 수 있으며, 여기서는 axis=1을 사용하여 두 번째 차원을 따라 합산합니다.
- A.sum(axis=1).shape: 합산된 결과 텐서의 모양(shape)을 확인하는 작업입니다. .shape 속성을 사용하여 모양을 확인합니다.
결과적으로, 코드를 실행하면 두 가지 결과가 반환됩니다:
- 첫 번째 결과는 원래 텐서 A의 모양(shape)을 나타내는 튜플입니다.
- 두 번째 결과는 두 번째 차원(행)을 따라 합산한 결과 텐서의 모양(shape)을 나타내는 튜플입니다. 이 결과 텐서는 두 번째 차원이 합산되었기 때문에 원래 텐서보다 한 차원이 줄어듭니다.
이 코드를 통해 PyTorch를 사용하여 텐서의 차원 및 차원 간의 연산을 조작하고 모양(shape)을 확인하는 방법을 이해할 수 있습니다.
(torch.Size([2, 3]), torch.Size([2]))
Reducing a matrix along both rows and columns via summation is equivalent to summing up all the elements of the matrix.
합산을 통해 행과 열 모두에서 행렬을 줄이는 것은 행렬의 모든 요소를 합산하는 것과 같습니다.
A.sum(axis=[0, 1]) == A.sum() # Same as A.sum()주어진 코드는 PyTorch 텐서 A에 대해 axis=[0, 1]를 사용하여 두 개의 축(차원)을 따라 합산한 결과와 전체 텐서를 합산한 결과를 비교하는 작업을 나타냅니다. 아래는 코드의 설명입니다:
- A.sum(axis=[0, 1]): 텐서 A에 대해 axis=[0, 1]을 사용하여 0번째 차원(열)과 1번째 차원(행)을 따라 합산한 결과를 계산합니다. 여기서 [0, 1]은 텐서의 0번째 차원과 1번째 차원을 모두 합산하라는 의미입니다. 결과는 전체 텐서의 합계를 나타내게 됩니다.
- A.sum(): 텐서 A의 모든 요소를 합산한 결과를 계산합니다. .sum() 메서드를 사용하면 텐서 내의 모든 요소를 합산한 결과가 반환됩니다.
- A.sum(axis=[0, 1]) == A.sum(): A.sum(axis=[0, 1])과 A.sum()의 결과를 비교하는 작업을 수행합니다. 두 결과가 같은지 여부를 확인하기 위한 비교 연산을 수행하며, 결과는 True 또는 False로 나타납니다.
결과적으로, 코드를 실행하면 A.sum(axis=[0, 1])과 A.sum()의 결과를 비교하여 두 값이 동일한지 여부를 확인하는 논리식이 반환됩니다. 이 코드는 텐서의 다차원 연산과 축을 따라 합산하는 방법을 보여주며, axis=[0, 1]을 사용하여 전체 텐서를 합산한 결과와 A.sum()를 사용한 결과가 동일함을 나타냅니다.
tensor(True)
A related quantity is the mean, also called the average. We calculate the mean by dividing the sum by the total number of elements. Because computing the mean is so common, it gets a dedicated library function that works analogously to sum.
관련 수량은 average 이라고도 하는 평균 mean 입니다. 합계를 전체 요소 수로 나누어 평균을 계산합니다. 평균을 계산하는 것은 매우 일반적이기 때문에 합계와 유사하게 작동하는 전용 라이브러리 함수를 얻습니다.
A.mean(), A.sum() / A.numel()주어진 코드는 PyTorch 텐서 A의 평균과 텐서의 모든 요소의 합계를 요소의 총 개수로 나눈 결과를 계산하는 작업을 나타냅니다. 아래는 코드의 설명입니다:
- A.mean(): 텐서 A의 평균을 계산합니다. .mean() 메서드를 사용하면 텐서 내의 모든 요소의 평균값이 반환됩니다.
- A.sum(): 텐서 A의 모든 요소를 합산한 결과를 계산합니다. .sum() 메서드를 사용하면 텐서 내의 모든 요소를 합산한 결과가 반환됩니다.
- A.numel(): 텐서 A의 요소의 총 개수를 계산합니다. .numel() 메서드는 텐서 내의 모든 요소의 개수를 반환합니다.
- A.sum() / A.numel(): A.sum()을 텐서의 요소 개수(A.numel())로 나눈 결과를 계산합니다. 이렇게 함으로써 텐서의 평균을 구합니다.
결과적으로, 코드를 실행하면 두 가지 결과가 반환됩니다:
- 첫 번째 결과는 텐서 A의 모든 요소의 평균값을 나타내는 값입니다. 이 값은 텐서의 모든 요소를 더하고 요소의 총 개수로 나눈 결과입니다.
- 두 번째 결과는 텐서 A의 모든 요소를 합산한 값을 나타내는 값입니다.
이 코드를 통해 PyTorch를 사용하여 텐서의 요소를 평균화하고 총합을 계산하는 방법을 이해할 수 있습니다.
(tensor(2.5000), tensor(2.5000))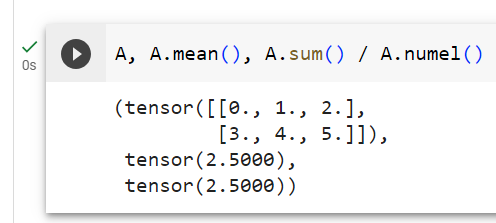
Likewise, the function for calculating the mean can also reduce a tensor along specific axes.
마찬가지로, 평균을 계산하는 함수는 특정 축을 따라 텐서를 줄일 수도 있습니다.
A.mean(axis=0), A.sum(axis=0) / A.shape[0]주어진 코드는 PyTorch 텐서 A에 대해 axis=0을 사용하여 0번째 차원(열)을 따라 평균과 합계를 계산한 결과를 비교하는 작업을 나타냅니다. 아래는 코드의 설명입니다:
- A.mean(axis=0): 텐서 A에 대해 axis=0을 사용하여 0번째 차원(열)을 따라 평균을 계산합니다. axis 매개변수를 사용하여 어떤 차원을 따라 평균을 계산할지 지정할 수 있으며, 여기서는 axis=0을 사용하여 0번째 차원(열)을 따라 평균을 계산합니다.
- A.sum(axis=0): 텐서 A에 대해 axis=0을 사용하여 0번째 차원(열)을 따라 합계를 계산합니다. axis 매개변수를 사용하여 어떤 차원을 따라 합계를 계산할지 지정할 수 있으며, 여기서는 axis=0을 사용하여 0번째 차원(열)을 따라 합계를 계산합니다.
- A.shape[0]: 텐서 A의 0번째 차원(열)의 크기를 확인합니다. A.shape은 텐서의 모양(shape)을 나타내는 튜플을 반환하며, 여기서 [0]을 사용하여 튜플의 첫 번째 요소를 얻습니다.
- A.sum(axis=0) / A.shape[0]: A.sum(axis=0)을 0번째 차원(열)의 크기(A.shape[0])로 나눈 결과를 계산합니다. 이렇게 함으로써 0번째 차원을 따라 합산한 평균을 구합니다.
결과적으로, 코드를 실행하면 두 가지 결과가 반환됩니다:
- 첫 번째 결과는 텐서 A의 0번째 차원(열)을 따라 평균을 계산한 결과입니다.
- 두 번째 결과는 텐서 A의 0번째 차원(열)을 따라 합산한 결과를 텐서의 0번째 차원 크기로 나눈 평균을 나타내는 값입니다.
이 코드를 통해 PyTorch를 사용하여 텐서의 특정 차원을 따라 평균 및 합계를 계산하고, 이를 텐서의 크기로 나누어 평균을 구하는 방법을 이해할 수 있습니다.
(tensor([1.5000, 2.5000, 3.5000]), tensor([1.5000, 2.5000, 3.5000]))
2.3.7. Non-Reduction Sum
Sometimes it can be useful to keep the number of axes unchanged when invoking the function for calculating the sum or mean. This matters when we want to use the broadcast mechanism.
때로는 합계 또는 평균을 계산하는 함수를 호출할 때 축 수를 변경하지 않고 유지하는 것이 유용할 수 있습니다. 이는 브로드캐스트 메커니즘을 사용하려는 경우 중요합니다.
sum_A = A.sum(axis=1, keepdims=True)
sum_A, sum_A.shape주어진 코드는 PyTorch 텐서 A에 대해 axis=1을 사용하여 1번째 차원(행)을 따라 합산한 결과를 계산하고, keepdims=True 옵션을 사용하여 결과 텐서의 차원을 유지한 채로 결과를 확인하는 작업을 나타냅니다. 아래는 코드의 설명입니다:
- A.sum(axis=1, keepdims=True): 텐서 A에 대해 axis=1을 사용하여 1번째 차원(행)을 따라 합산한 결과를 계산합니다. axis 매개변수를 사용하여 어떤 차원을 따라 합산할지 지정할 수 있으며, 여기서는 axis=1을 사용하여 1번째 차원(행)을 따라 합산합니다. keepdims=True 옵션은 결과 텐서의 차원을 유지하도록 설정합니다.
- sum_A: 합산 결과를 저장하는 변수로 A.sum(axis=1, keepdims=True)의 결과를 할당합니다.
- sum_A.shape: sum_A 텐서의 모양(shape)을 확인합니다. .shape 속성을 사용하면 텐서의 차원과 각 차원의 크기를 나타내는 튜플을 반환합니다.
결과적으로, 코드를 실행하면 두 가지 결과가 반환됩니다:
- 첫 번째 결과는 텐서 A의 1번째 차원(행)을 따라 합산한 결과를 나타내는 텐서입니다. 이 텐서의 차원은 원래 텐서와 동일한 차원을 가지며, 합산 결과가 유지됩니다.
- 두 번째 결과는 sum_A 텐서의 모양(shape)을 나타내는 튜플입니다.
이 코드를 통해 PyTorch를 사용하여 텐서의 특정 차원을 따라 합산하고, 결과 텐서의 차원을 유지하며 차원의 모양(shape)을 확인하는 방법을 이해할 수 있습니다.
(tensor([[ 3.],
[12.]]),
torch.Size([2, 1]))
For instance, since sum_A keeps its two axes after summing each row, we can divide A by sum_A with broadcasting to create a matrix where each row sums up to 1.
예를 들어 sum_A는 각 행을 합산한 후 두 개의 축을 유지하므로 브로드캐스팅을 통해 A를 sum_A로 나누어 각 행의 합이 다음과 같은 행렬을 만들 수 있습니다.
A / sum_A주어진 코드는 PyTorch 텐서 A를 sum_A로 나누는 작업을 나타냅니다. sum_A는 이전 코드에서 A의 1번째 차원(행)을 따라 합산한 결과를 나타내는 텐서입니다. 아래는 코드의 설명입니다:
- A / sum_A: 텐서 A를 sum_A로 나누는 작업을 수행합니다. 이 작업은 요소별로 (element-wise) 이루어지며, 텐서 A와 sum_A의 같은 위치에 있는 요소끼리 나눗셈을 수행합니다. 결과는 새로운 텐서로 반환됩니다.
결과적으로, 코드를 실행하면 A와 sum_A의 요소별 나눗셈 연산을 수행한 결과인 새로운 텐서가 반환됩니다. 이 코드를 통해 텐서의 요소끼리 나눗셈 연산을 수행하는 방법을 이해할 수 있습니다. 이러한 연산을 사용하면 데이터 정규화나 스케일링과 같은 다양한 작업을 수행할 수 있습니다.
tensor([[0.0000, 0.3333, 0.6667],
[0.2500, 0.3333, 0.4167]])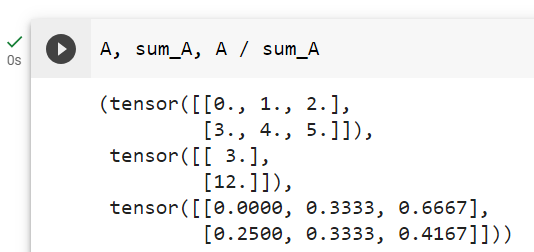
If we want to calculate the cumulative sum of elements of A along some axis, say axis=0 (row by row), we can call the cumsum function. By design, this function does not reduce the input tensor along any axis.
어떤 축(축=0(행 단위))을 따라 A 요소의 누적 합계를 계산하려면 cumsum 함수를 호출할 수 있습니다. 설계상 이 함수는 어떤 축에서도 입력 텐서를 줄이지 않습니다.
A.cumsum(axis=0)주어진 코드는 PyTorch 텐서 A에 대해 axis=0을 사용하여 0번째 차원(열)을 따라 누적 합계(cumulative sum)를 계산하는 작업을 나타냅니다. 아래는 코드의 설명입니다:
- A.cumsum(axis=0): 텐서 A에 대해 axis=0을 사용하여 0번째 차원(열)을 따라 누적 합계를 계산합니다. axis 매개변수를 사용하여 어떤 차원을 따라 누적 합계를 계산할지 지정할 수 있으며, 여기서는 axis=0을 사용하여 0번째 차원(열)을 따라 누적 합계를 계산합니다.
결과적으로, 코드를 실행하면 텐서 A의 0번째 차원(열)을 따라 누적 합계를 계산한 결과를 반환합니다. 이 결과 텐서는 원래 텐서와 동일한 모양(shape)을 가지며, 각 요소는 해당 열까지의 누적 합계를 나타냅니다.
이 코드를 통해 PyTorch를 사용하여 텐서의 특정 차원을 따라 누적 합계를 계산하는 방법을 이해할 수 있습니다. 누적 합계는 주어진 차원의 각 위치에서 해당 위치까지의 합계를 나타내는데 사용됩니다.
tensor([[0., 1., 2.],
[3., 5., 7.]])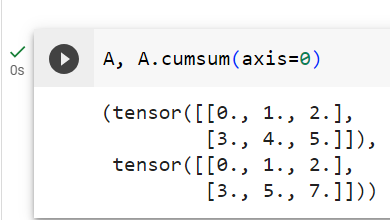
2.3.8. Dot Products
So far, we have only performed elementwise operations, sums, and averages. And if this was all we could do, linear algebra would not deserve its own section. Fortunately, this is where things get more interesting. One of the most fundamental operations is the dot product. Given two vectors x,y∈ ℝ d, their dot product x⊤y (also known as inner product, ⟨x,y⟩) is a sum over the products of the elements at the same position: x⊤y=∑d i=1 xiyi.
지금까지는 요소별 연산, 합계, 평균만 수행했습니다. 그리고 이것이 우리가 할 수 있는 전부라면 선형 대수학은 그 자체의 섹션을 가질 자격이 없을 것입니다. 다행히도 여기서 상황이 더욱 흥미로워집니다. 가장 기본적인 연산 중 하나는 내적(dot product)입니다. 두 개의 벡터 x,y∈ ℝd가 주어지면, 그 내적 x⊤y(내적이라고도 함, ⟨x,y⟩)는 동일한 위치에 있는 요소의 곱에 대한 합입니다. x⊤y=∑d i=1 xiyi.
y = torch.ones(3, dtype = torch.float32)
x, y, torch.dot(x, y)주어진 코드는 PyTorch를 사용하여 두 벡터 x와 y를 생성하고, 이 두 벡터의 내적(dot product)을 계산하는 작업을 나타냅니다. 아래는 코드의 설명입니다:
- y = torch.ones(3, dtype=torch.float32): 길이가 3인 1차원 텐서 y를 생성합니다. torch.ones() 함수를 사용하여 모든 요소가 1로 초기화된 텐서를 생성하며, dtype 매개변수를 사용하여 데이터 타입을 부동소수점(float32)으로 설정합니다.
- x: 벡터 x를 생성한 변수입니다. 코드에서 직접 표시되지 않았지만, x는 이전에 어떤 값으로 초기화되었을 것입니다. x는 y와 동일한 길이를 가져야합니다.
- y: 위에서 생성한 벡터 y입니다.
- torch.dot(x, y): 벡터 x와 y 사이의 내적(dot product)을 계산합니다. 내적은 두 벡터의 대응하는 요소를 곱한 후 모두 더한 값을 의미합니다. 이 코드는 x와 y 벡터의 내적을 계산하고 결과를 반환합니다.
결과적으로, 코드를 실행하면 x와 y 벡터가 생성되고, 이 두 벡터의 내적이 계산되어 반환됩니다. 내적은 벡터 간의 유사성을 측정하는 데 사용되며, 벡터의 각 성분을 곱한 후 모두 합한 값으로 표현됩니다.
(tensor([0., 1., 2.]), tensor([1., 1., 1.]), tensor(3.))
Equivalently, we can calculate the dot product of two vectors by performing an elementwise multiplication followed by a sum:
마찬가지로 요소별 곱셈과 합을 수행하여 두 벡터의 내적을 계산할 수 있습니다.
torch.sum(x * y)주어진 코드는 PyTorch를 사용하여 두 벡터 x와 y를 요소별로 곱하고 그 결과를 모두 합산하는 작업을 나타냅니다. 코드에서 올바른 방법으로 작성하기 위해서는 torch.sum() 함수를 사용해야 합니다. 아래는 코드의 설명입니다:
- torch.sum(x * y): 벡터 x와 y의 요소별 곱셈을 수행한 후, 그 결과를 모두 합산합니다. 이 코드는 x와 y의 각 성분을 곱한 후 그 결과를 모두 합산하는 동작을 수행합니다.
결과적으로, 코드를 실행하면 두 벡터 x와 y의 요소별 곱셈 결과가 계산되고, 이 결과를 모두 합산한 값이 반환됩니다. 내적과 유사하지만 내적은 두 벡터의 대응하는 요소를 곱한 후 모두 더하는 것이며, 이 코드는 요소별 곱셈 결과를 모두 더합니다.
tensor(3.)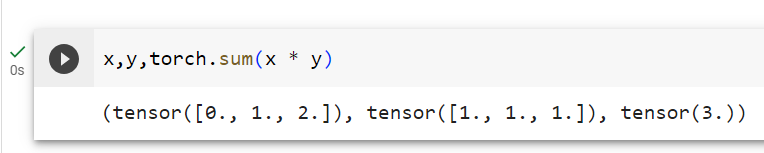
Dot products are useful in a wide range of contexts. For example, given some set of values, denoted by a vector x∈ ℝn, and a set of weights, denoted by w∈ ℝ n , the weighted sum of the values in x according to the weights w could be expressed as the dot product x⊤w. When the weights are nonnegative and sum to 1, i.e., (∑ni=1 wi=1), the dot product expresses a weighted average. After normalizing two vectors to have unit length, the dot products express the cosine of the angle between them. Later in this section, we will formally introduce this notion of length.
내적은 다양한 상황에서 유용합니다. 예를 들어, 벡터 x∈ ℝ n으로 표시되는 일부 값 세트와 w∈ ℝ n으로 표시되는 가중치 세트가 주어지면 가중치 w에 따른 x 값의 가중 합은 점으로 표현될 수 있습니다. 제품 x⊤w. 가중치가 음수가 아니고 합이 1인 경우, 즉 (∑n i=1 wi=1), 내적은 가중 평균을 나타냅니다. 두 벡터를 단위 길이로 정규화한 후, 내적은 두 벡터 사이의 각도의 코사인을 나타냅니다. 이 섹션의 뒷부분에서 길이에 대한 개념을 공식적으로 소개하겠습니다.
2.3.9. Matrix–Vector Products
Now that we know how to calculate dot products, we can begin to understand the product between an m×n matrix A and an n-dimensional vector x. To start off, we visualize our matrix in terms of its row vectors where each a⊤i∈ ℝn is a row vector representing the i th row of the matrix A.
이제 내적을 계산하는 방법을 알았으므로 m×n 행렬 A와 n차원 벡터 x 사이의 곱을 이해할 수 있습니다. 시작하려면 각 a⊤i∈ ℝn이 행렬 A의 i번째 행을 나타내는 행 벡터인 행 벡터 측면에서 행렬을 시각화합니다.

The matrix–vector product Ax is simply a column vector of length m, whose i th element is the dot product a⊤i x:
행렬-벡터 곱 Ax는 단순히 길이가 m인 열 벡터이며, i 번째 요소는 내적 a⊤i x입니다.
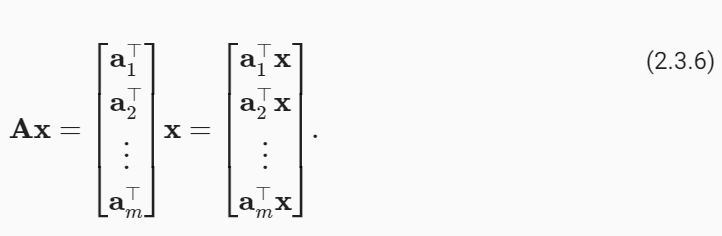
We can think of multiplication with a matrix A∈ ℝm×n as a transformation that projects vectors from ℝn to ℝm. These transformations are remarkably useful. For example, we can represent rotations as multiplications by certain square matrices. Matrix–vector products also describe the key calculation involved in computing the outputs of each layer in a neural network given the outputs from the previous layer.
행렬 A∈ ℝ m×n을 사용한 곱셈을 ℝn에서 ℝm으로 벡터를 투영하는 변환으로 생각할 수 있습니다. 이러한 변환은 매우 유용합니다. 예를 들어 회전을 특정 정사각 행렬의 곱셈으로 표현할 수 있습니다. 행렬-벡터 곱은 이전 계층의 출력을 바탕으로 신경망의 각 계층 출력을 계산하는 데 관련된 주요 계산도 설명합니다.
To express a matrix–vector product in code, we use the mv function. Note that the column dimension of A (its length along axis 1) must be the same as the dimension of x (its length). Python has a convenience operator @ that can execute both matrix–vector and matrix–matrix products (depending on its arguments). Thus we can write A@x.
행렬-벡터 곱을 코드로 표현하기 위해 mv 함수를 사용합니다. A의 열 치수(축 1을 따른 길이)는 x의 치수(길이)와 동일해야 합니다. Python에는 행렬-벡터 및 행렬-행렬 곱을 모두 실행할 수 있는 편리한 연산자 @가 있습니다(인수에 따라 다름). 따라서 우리는 A@x를 쓸 수 있습니다.
A.shape, x.shape, torch.mv(A, x), A@x주어진 코드는 PyTorch를 사용하여 행렬-벡터 곱셈을 수행하는 작업을 나타냅니다. 코드에서 A는 행렬이고, x는 벡터입니다. 코드는 두 가지 다른 방법으로 행렬 A와 벡터 x를 곱셈하고, 그 결과를 비교합니다. 아래는 코드의 설명입니다:
- A.shape: 행렬 A의 모양(shape)을 확인하는 작업입니다. .shape 속성을 사용하면 행렬의 차원과 각 차원의 크기를 나타내는 튜플이 반환됩니다.
- x.shape: 벡터 x의 모양(shape)을 확인하는 작업입니다. .shape 속성을 사용하면 벡터의 차원과 크기를 나타내는 튜플이 반환됩니다.
- torch.mv(A, x): 행렬-벡터 곱셈을 수행하는 함수입니다. 이 함수는 행렬 A와 벡터 x를 곱셈하고 결과 벡터를 반환합니다. mv는 "matrix-vector"의 약자입니다.
- A @ x: Python에서는 @ 연산자를 사용하여 행렬-벡터 곱셈을 간결하게 나타낼 수 있습니다. 이 코드는 행렬 A와 벡터 x를 곱셈하고 결과 벡터를 반환합니다.
결과적으로, 코드를 실행하면 다음 네 가지 결과가 반환됩니다:
- 첫 번째 결과는 행렬 A의 모양(shape)을 나타내는 튜플입니다.
- 두 번째 결과는 벡터 x의 모양(shape)을 나타내는 튜플입니다.
- 세 번째 결과는 torch.mv(A, x)를 사용하여 계산된 행렬-벡터 곱셈의 결과 벡터입니다.
- 네 번째 결과는 A @ x를 사용하여 계산된 행렬-벡터 곱셈의 결과 벡터로, 두 번째 결과와 동일해야 합니다.
이 코드는 행렬과 벡터 간의 곱셈을 수행하는 방법을 보여주며, Python에서 제공되는 간결한 @ 연산자를 사용하여도 동일한 결과를 얻을 수 있습니다.
(torch.Size([2, 3]), torch.Size([3]), tensor([ 5., 14.]), tensor([ 5., 14.]))
2.3.10. Matrix–Matrix Multiplication
Once you have gotten the hang of dot products and matrix–vector products, then matrix–matrix multiplication should be straightforward.
내적과 행렬-벡터 곱에 익숙해지면 행렬-행렬 곱셈이 간단해집니다.
Say that we have two matrices A∈ ℝn×k and B∈ ℝ k×m:
두 개의 행렬 A∈ ℝ n×k와 B∈ ℝ k×m이 있다고 가정해 보겠습니다.
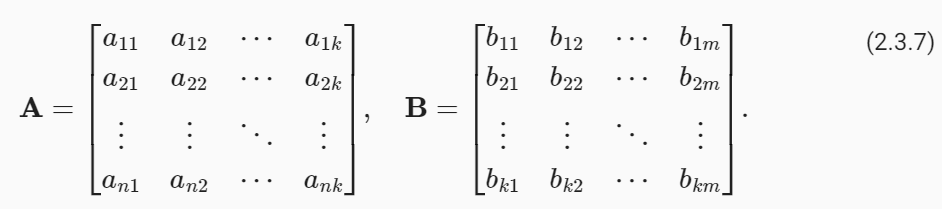
Let a⊤i∈ ℝk denote the row vector representing the i th row of the matrix A and let bj∈ ℝk denote the column vector from the j th column of the matrix B:
a⊤i∈ ℝk가 행렬 A의 i번째 행을 나타내는 행 벡터를 나타내고 bj∈ ℝk가 행렬 B의 j번째 열의 열 벡터를 나타낸다고 가정합니다.

To form the matrix product C∈ ℝ m×n, we simply compute each element cij as the dot product between the i th row of A and the j th column of B, i.e., a⊤ibj:
행렬 곱 C∈ ℝm×n을 형성하기 위해 각 요소 cij를 A의 i번째 행과 B의 j번째 열 사이의 내적, 즉 a⊤ibj로 간단히 계산합니다.
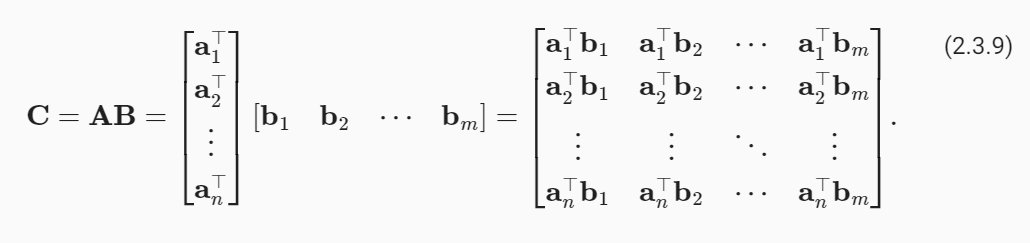
We can think of the matrix–matrix multiplication AB as performing m matrix–vector products or m×n dot products and stitching the results together to form an n×m matrix. In the following snippet, we perform matrix multiplication on A and B. Here, A is a matrix with two rows and three columns, and B is a matrix with three rows and four columns. After multiplication, we obtain a matrix with two rows and four columns.
행렬-행렬 곱셈 AB는 m개의 행렬-벡터 곱 또는 m×n 도트 곱을 수행하고 그 결과를 함께 연결하여 n×m 행렬을 형성하는 것으로 생각할 수 있습니다. 다음 코드에서는 A와 B에 대해 행렬 곱셈을 수행합니다. 여기서 A는 행 2개와 열 3개로 구성된 행렬이고 B는 행 3개와 열 4개로 구성된 행렬입니다. 곱셈을 하면 2개의 행과 4개의 열이 있는 행렬을 얻습니다.
B = torch.ones(3, 4)
torch.mm(A, B), A@B주어진 코드는 PyTorch를 사용하여 두 행렬 A와 B의 행렬-행렬 곱셈을 수행하는 작업을 나타냅니다. 코드는 두 가지 다른 방법으로 행렬-행렬 곱셈을 수행하고, 그 결과를 비교합니다. 아래는 코드의 설명입니다:
- B = torch.ones(3, 4): 3x4 크기의 모든 요소가 1로 초기화된 행렬 B를 생성합니다.
- torch.mm(A, B): torch.mm() 함수를 사용하여 두 행렬 A와 B의 행렬-행렬 곱셈을 계산합니다. 이 함수는 두 행렬의 행렬-행렬 곱셈을 수행하고 결과 행렬을 반환합니다.
- A @ B: Python에서는 @ 연산자를 사용하여 행렬-행렬 곱셈을 간결하게 나타낼 수 있습니다. 이 코드는 두 행렬 A와 B의 행렬-행렬 곱셈을 계산하고 결과 행렬을 반환합니다.
결과적으로, 코드를 실행하면 다음 네 가지 결과가 반환됩니다:
- 첫 번째 결과는 torch.mm(A, B)를 사용하여 계산된 행렬-행렬 곱셈의 결과 행렬입니다.
- 두 번째 결과는 A @ B를 사용하여 계산된 행렬-행렬 곱셈의 결과 행렬로, 첫 번째 결과와 동일해야 합니다.
이 코드는 PyTorch를 사용하여 행렬-행렬 곱셈을 수행하는 방법을 보여주며, Python에서 제공되는 @ 연산자를 사용하여도 동일한 결과를 얻을 수 있습니다.
(tensor([[ 3., 3., 3., 3.],
[12., 12., 12., 12.]]),
tensor([[ 3., 3., 3., 3.],
[12., 12., 12., 12.]]))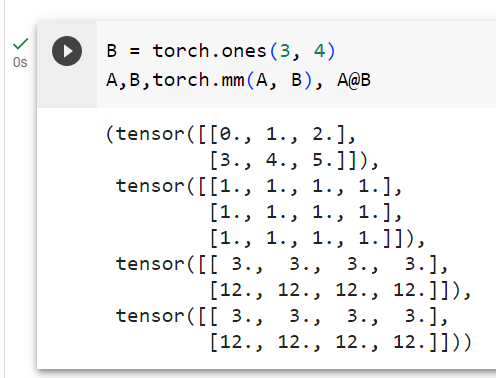
The term matrix–matrix multiplication is often simplified to matrix multiplication, and should not be confused with the Hadamard product.
행렬-행렬 곱셈이라는 용어는 행렬 곱셈으로 단순화되는 경우가 많으므로 Hadamard 곱과 혼동해서는 안 됩니다.
2.3.11. Norms
Some of the most useful operators in linear algebra are norms. Informally, the norm of a vector tells us how big it is. For instance, the ℓ2 norm measures the (Euclidean) length of a vector. Here, we are employing a notion of size that concerns the magnitude of a vector’s components (not its dimensionality).
선형 대수학에서 가장 유용한 연산자 중 일부는 norms 입니다. 비공식적으로 벡터의 노름(Norm)은 벡터가 얼마나 큰지 알려줍니다. 예를 들어, ℓ2 노름은 벡터의 (유클리드) 길이를 측정합니다. 여기서는 벡터 구성 요소의 크기(차원이 아닌)와 관련된 크기 개념을 사용합니다.
A norm is a function ‖⋅‖ that maps a vector to a scalar and satisfies the following three properties:
노름(Norm)은 벡터를 스칼라에 매핑하고 다음 세 가지 속성을 충족하는 함수 ‖⋅‖ 입니다.
- Given any vector x, if we scale (all elements of) the vector by a scalar α ∈ ℝ , its norm scales accordingly:
벡터 x가 주어지면 벡터의 모든 요소를 스칼라 α ∈ ℝ로 스케일링하면 해당 노름도 그에 따라 스케일링됩니다.

2. For any vectors x and y: norms satisfy the triangle inequality:
2. 모든 벡터 x 및 y에 대해: 노름은 삼각형 부등식을 충족합니다.

3. The norm of a vector is nonnegative and it only vanishes if the vector is zero:
3. 벡터의 노름은 음수가 아니며 벡터가 0인 경우에만 사라집니다.

Many functions are valid norms and different norms encode different notions of size. The Euclidean norm that we all learned in elementary school geometry when calculating the hypotenuse of a right triangle is the square root of the sum of squares of a vector’s elements. Formally, this is called the ℓ2 norm and expressed as
많은 함수는 유효한 norms 이며, 서로 다른 norms 은 서로 다른 크기 개념을 인코딩합니다. 우리가 초등학교 기하학에서 직각삼각형의 빗변을 계산할 때 배운 유클리드 표준은 벡터 요소의 제곱합의 제곱근입니다. 공식적으로 이를 ℓ2 표준이라고 하며 다음과 같이 표현됩니다.

Norms 란?
In mathematics, and more specifically in linear algebra, "norms" refer to functions that assign a positive length or size to vectors (including points in Euclidean space) or other objects. Norms are used to quantify the magnitude or size of an object, and they have various applications in mathematics, physics, engineering, and computer science.
수학에서 "노름(norms)"은 벡터(유클리드 공간의 점을 포함한) 또는 다른 객체에 길이 또는 크기를 할당하는 함수를 의미합니다. 노름은 객체의 크기 또는 크기를 양의 값으로 표현하며, 수학, 물리학, 공학 및 컴퓨터 과학의 다양한 분야에서 응용됩니다.
There are different types of norms, but the most common one is the Euclidean norm, also known as the L2 norm. The Euclidean norm of a vector is calculated by taking the square root of the sum of the squares of its components. In 2D space, it corresponds to the length of a vector from the origin to a point in the plane. In n-dimensional space, it generalizes to:
노름의 다양한 유형이 있지만, 가장 일반적인 것은 유클리드 노름 또는 L2 노름입니다. 벡터의 유클리드 노름은 구성 요소의 제곱의 합의 제곱근을 취하여 계산됩니다. 2차원 공간에서 이것은 평면상의 한 점에서 원점까지의 벡터의 길이에 해당합니다. n차원 공간에서 일반화됩니다:
L2 Norm or Euclidean Norm of a vector x = (x1, x2, ..., xn) is defined as:
벡터 x = (x1, x2, ..., xn)의 L2 노름 또는 유클리드 노름은 다음과 같이 정의됩니다:
||x||₂ = √(x1² + x2² + ... + xn²)
Other common norms include the L1 norm, which is the sum of the absolute values of the components, and the infinity norm (L∞ norm), which is the maximum absolute value of any component. There are other norms as well, such as the Lp norms, which generalize the L1 and L2 norms.
다른 일반적인 노름에는 L1 노름이 있으며, 이것은 구성 요소의 절대값의 합입니다. 그리고 무한대 노름 (L∞ 노름)은 어떤 구성 요소의 최대 절대값입니다. Lp 노름과 같은 다른 노름도 있으며, L1 및 L2 노름을 일반화합니다.
Norms have various applications in machine learning, optimization, signal processing, and many other fields. They are used to measure distances, define regularization terms in machine learning models, and assess the convergence of iterative algorithms, among other things. The choice of norm depends on the specific problem and the properties you want to capture.
노름은 머신러닝, 최적화, 신호 처리 및 기타 다양한 분야에서 응용됩니다. 거리 측정, 머신러닝 모델에서 정규화 용어를 정의하고 반복 알고리즘의 수렴을 평가하는 등 다양한 목적으로 사용됩니다. 노름의 선택은 특정 문제와 캡처하려는 특성에 따라 다릅니다.
The method norm calculates the ℓ2 norm.
method 노름은 ℓ2 노름을 계산합니다.
u = torch.tensor([3.0, -4.0])
torch.norm(u)주어진 코드는 PyTorch를 사용하여 2차원 벡터 u의 L2 노름(유클리드 노름)을 계산하는 작업을 나타냅니다. 아래는 코드의 설명입니다:
- u = torch.tensor([3.0, -4.0]): 길이가 2인 1차원 텐서 u를 생성합니다. 이 벡터는 두 개의 요소로 구성되며, [3.0, -4.0]으로 초기화됩니다. 이러한 벡터는 평면 상의 점을 나타낼 수 있습니다.
- torch.norm(u): PyTorch의 torch.norm() 함수를 사용하여 벡터 u의 L2 노름을 계산합니다. L2 노름은 벡터의 모든 요소의 제곱을 합산한 후 그 합의 제곱근을 취한 것으로, 벡터의 크기나 길이를 나타냅니다.
결과적으로, 코드를 실행하면 u 벡터의 L2 노름이 계산되고 그 값이 반환됩니다. 이것은 원점(0, 0)에서 벡터 u의 끝점까지의 거리를 나타내며, L2 노름은 일반적으로 벡터의 크기를 계산하는 데 사용됩니다.
tensor(5.)
The ℓ1 norm is also common and the associated measure is called the Manhattan distance. By definition, the ℓ1 norm sums the absolute values of a vector’s elements:
ℓ1 노름도 일반적이며 관련 측정값을 맨해튼 거리라고 합니다. 정의에 따르면 ℓ1 노름은 벡터 요소의 절대값을 합산합니다.

Compared to the ℓ2 norm, it is less sensitive to outliers. To compute the ℓ1 norm, we compose the absolute value with the sum operation.
ℓ2 norm 에 비해 이상값에 덜 민감합니다. ℓ1 노름을 계산하기 위해 합계 연산을 통해 절대값을 구성합니다.
torch.abs(u).sum()주어진 코드는 PyTorch를 사용하여 벡터 u의 각 요소의 절댓값을 계산하고, 이 절댓값들을 모두 더하는 작업을 나타냅니다. 아래는 코드의 설명입니다:
- torch.Abs(u): torch.Abs() 함수를 사용하여 벡터 u의 각 요소의 절댓값을 계산합니다. 이 함수는 각 요소를 양수로 만들어줍니다.
- .sum(): .sum() 메서드를 사용하여 절댓값이 계산된 벡터의 모든 요소를 더합니다. 이로써 벡터의 각 요소의 절댓값의 총합을 얻을 수 있습니다.
결과적으로, 코드를 실행하면 u 벡터의 각 요소의 절댓값을 계산하고, 그 절댓값들을 모두 더한 값이 반환됩니다. 이것은 벡터의 모든 요소의 절댓값을 합산하여 얻은 값으로, 해당 벡터의 크기나 길이를 나타냅니다.
tensor(7.)
Both the ℓ2 and ℓ1 norms are special cases of the more general ℓp norms:
ℓ2 및 ℓ1 노름은 모두 보다 일반적인 ℓp 노름의 특별한 경우입니다.

In the case of matrices, matters are more complicated. After all, matrices can be viewed both as collections of individual entries and as objects that operate on vectors and transform them into other vectors. For instance, we can ask by how much longer the matrix–vector product Xv could be relative to v. This line of thought leads to what is called the spectral norm. For now, we introduce the Frobenius norm, which is much easier to compute and defined as the square root of the sum of the squares of a matrix’s elements:
행렬의 경우 문제는 더 복잡합니다. 결국 행렬은 개별 항목의 모음으로 볼 수도 있고 벡터에 대해 연산을 수행하고 이를 다른 벡터로 변환하는 개체로 볼 수도 있습니다. 예를 들어, 행렬-벡터 곱 Xv가 v에 비해 얼마나 더 길 수 있는지 물어볼 수 있습니다. 이러한 생각은 스펙트럼 표준이라고 불리는 것으로 이어집니다. 지금은 계산하기가 훨씬 쉽고 행렬 요소의 제곱합의 제곱근으로 정의되는 프로베니우스 노름(Frobenius Norm)을 소개합니다.

The Frobenius norm behaves as if it were an ℓ2 norm of a matrix-shaped vector. Invoking the following function will calculate the Frobenius norm of a matrix.
Frobenius 노름은 마치 행렬 모양 벡터의 ℓ2 노름인 것처럼 동작합니다. 다음 함수를 호출하면 행렬의 Frobenius 표준이 계산됩니다.
torch.norm(torch.ones((4, 9)))주어진 코드는 PyTorch를 사용하여 4x9 크기의 모든 요소가 1로 초기화된 행렬을 생성하고, 이 행렬의 L2 노름(유클리드 노름)을 계산하는 작업을 나타냅니다. 아래는 코드의 설명입니다:
- torch.ones((4, 9)): 4x9 크기의 모든 요소가 1로 초기화된 행렬을 생성합니다. torch.ones() 함수를 사용하여 모든 요소가 1인 행렬을 생성할 수 있으며, 입력 매개변수로 원하는 크기 (여기서는 4x9)를 지정합니다.
- torch.norm(...): torch.norm() 함수를 사용하여 생성한 4x9 행렬의 L2 노름을 계산합니다. L2 노름은 행렬의 각 요소의 제곱을 합산한 후 그 합의 제곱근을 취한 것으로, 행렬의 크기나 길이를 나타냅니다.
결과적으로, 코드를 실행하면 4x9 크기의 행렬의 L2 노름이 계산되고 그 값이 반환됩니다. 이것은 행렬의 크기나 길이를 나타내며, 모든 요소가 1인 행렬의 경우에는 행렬의 크기와 동일한 값을 가집니다.
tensor(6.)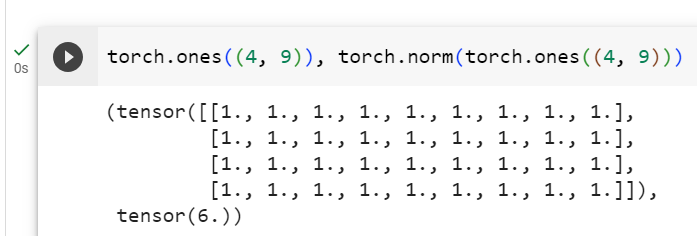
While we do not want to get too far ahead of ourselves, we already can plant some intuition about why these concepts are useful. In deep learning, we are often trying to solve optimization problems: maximize the probability assigned to observed data; maximize the revenue associated with a recommender model; minimize the distance between predictions and the ground truth observations; minimize the distance between representations of photos of the same person while maximizing the distance between representations of photos of different people. These distances, which constitute the objectives of deep learning algorithms, are often expressed as norms.
우리는 너무 앞서나가고 싶지 않지만 이러한 개념이 왜 유용한지에 대한 직관을 이미 심을 수 있습니다. 딥러닝에서 우리는 종종 최적화 문제를 해결하려고 노력합니다. 관찰된 데이터에 할당된 확률을 최대화합니다. 추천 모델과 관련된 수익을 극대화합니다. 예측과 실제 관찰 사이의 거리를 최소화합니다. 같은 사람의 사진 표현 사이의 거리를 최소화하는 동시에 다른 사람의 사진 표현 사이의 거리를 최대화합니다. 딥러닝 알고리즘의 목표를 구성하는 이러한 거리는 종종 norms 으로 표현됩니다.
2.3.12. Discussion
In this section, we have reviewed all the linear algebra that you will need to understand a significant chunk of modern deep learning. There is a lot more to linear algebra, though, and much of it is useful for machine learning. For example, matrices can be decomposed into factors, and these decompositions can reveal low-dimensional structure in real-world datasets. There are entire subfields of machine learning that focus on using matrix decompositions and their generalizations to high-order tensors to discover structure in datasets and solve prediction problems. But this book focuses on deep learning. And we believe you will be more inclined to learn more mathematics once you have gotten your hands dirty applying machine learning to real datasets. So while we reserve the right to introduce more mathematics later on, we wrap up this section here.
이 섹션에서는 현대 딥러닝의 상당 부분을 이해하는 데 필요한 모든 선형 대수학을 검토했습니다. 하지만 선형 대수학에는 더 많은 내용이 있으며 그 중 대부분은 기계 학습에 유용합니다. 예를 들어, 행렬은 요인으로 분해될 수 있으며 이러한 분해는 실제 데이터세트의 저차원 구조를 드러낼 수 있습니다. 행렬 분해와 고차 텐서에 대한 일반화를 사용하여 데이터 세트의 구조를 발견하고 예측 문제를 해결하는 데 초점을 맞춘 기계 학습의 전체 하위 필드가 있습니다. 하지만 이 책은 딥러닝에 중점을 두고 있습니다. 그리고 실제 데이터 세트에 기계 학습을 적용해 본 후에는 더 많은 수학을 배우고 싶은 마음이 더 커질 것이라고 믿습니다. 따라서 나중에 더 많은 수학을 소개할 권리가 있지만 여기에서 이 섹션을 마무리합니다.
If you are eager to learn more linear algebra, there are many excellent books and online resources. For a more advanced crash course, consider checking out Strang (1993), Kolter (2008), and Petersen and Pedersen (2008).
선형 대수학을 더 배우고 싶다면 훌륭한 책과 온라인 리소스가 많이 있습니다. 보다 고급 집중 과정을 보려면 Strang(1993), Kolter(2008), Petersen 및 Pedersen(2008)을 확인해 보세요.
To recap: 요약하자면:
- Scalars, vectors, matrices, and tensors are the basic mathematical objects used in linear algebra and have zero, one, two, and an arbitrary number of axes, respectively.
- 스칼라, 벡터, 행렬 및 텐서는 선형 대수학에 사용되는 기본 수학적 객체이며 각각 0, 1, 2 및 임의 개수의 축을 갖습니다.
- Tensors can be sliced or reduced along specified axes via indexing, or operations such as sum and mean, respectively.
- 텐서는 인덱싱이나 합계 및 평균과 같은 연산을 통해 지정된 축을 따라 분할하거나 축소할 수 있습니다.
- Elementwise products are called Hadamard products. By contrast, dot products, matrix–vector products, and matrix–matrix products are not elementwise operations and in general return objects having shapes that are different from the the operands.
- Elementwise products 을 Hadamard products 이라고 합니다. 대조적으로, 내적, 행렬-벡터 곱, 행렬-행렬 곱은 요소별 연산이 아니며 일반적으로 피연산자와 다른 모양을 갖는 객체를 반환합니다.
- Compared to Hadamard products, matrix–matrix products take considerably longer to compute (cubic rather than quadratic time).
- Hadamard 곱과 비교하여 행렬-행렬 곱은 계산하는 데 상당히 오랜 시간이 걸립니다(2차 시간이 아닌 3차 시간).
- Norms capture various notions of the magnitude of a vector (or matrix), and are commonly applied to the difference of two vectors to measure their distance apart.
- Norms는 벡터(또는 행렬)의 크기에 대한 다양한 개념을 포착하며 일반적으로 두 벡터의 차이에 적용되어 거리를 측정합니다.
- Common vector norms include the ℓ1 and ℓ2 norms, and common matrix norms include the spectral and Frobenius norms.
- 공통 벡터 노름에는 ℓ1 및 ℓ2 노름이 포함되고, 공통 행렬 노름에는 스펙트럼 및 프로베니우스 노름이 포함됩니다.

'Dive into Deep Learning > D2L Preliminaries' 카테고리의 다른 글
| D2L - 2.7. Documentation (2) | 2023.10.14 |
|---|---|
| D2L - 2.6. Probability and Statistics (0) | 2023.10.14 |
| D2L - 2.5. Automatic Differentiation (0) | 2023.10.12 |
| D2L - 2.4. Calculus : 미적분 (1) | 2023.10.12 |
| D2L - 2.2. Data Preprocessing (0) | 2023.10.09 |
| D2L - 2.1. Data Manipulation (0) | 2023.10.09 |
| D2L - 2. Preliminaries (0) | 2023.10.09 |
