https://d2l.ai/chapter_preliminaries/calculus.html
2.4. Calculus — Dive into Deep Learning 1.0.3 documentation
d2l.ai
2.4. Calculus
For a long time, how to calculate the area of a circle remained a mystery. Then, in Ancient Greece, the mathematician Archimedes came up with the clever idea to inscribe a series of polygons with increasing numbers of vertices on the inside of a circle (Fig. 2.4.1). For a polygon with n vertices, we obtain n triangles. The height of each triangle approaches the radius r as we partition the circle more finely. At the same time, its base approaches 2 π r/n, since the ratio between arc and secant approaches 1 for a large number of vertices. Thus, the area of the polygon approaches n⋅r⋅1/2(2 π r /n)= π r **2.
오랫동안 원의 넓이를 계산하는 방법은 미스터리로 남아 있었습니다. 그런 다음 고대 그리스의 수학자 아르키메데스는 원 내부에 정점 수가 증가하는 일련의 다각형을 새기는 영리한 아이디어를 생각해 냈습니다(그림 2.4.1). n개의 꼭지점을 가진 다각형의 경우 n개의 삼각형을 얻습니다. 원을 더 세밀하게 분할할수록 각 삼각형의 높이는 반지름 r에 가까워집니다. 동시에, 그 밑변은 2π r/n에 가까워집니다. 왜냐하면 호와 시컨트 사이의 비율이 많은 수의 꼭지점에 대해 1에 가까워지기 때문입니다. 따라서 다각형의 면적은 n⋅r⋅1/2(2 π r /n)= π r **2에 가까워집니다.

This limiting procedure is at the root of both differential calculus and integral calculus. The former can tell us how to increase or decrease a function’s value by manipulating its arguments. This comes in handy for the optimization problems that we face in deep learning, where we repeatedly update our parameters in order to decrease the loss function. Optimization addresses how to fit our models to training data, and calculus is its key prerequisite. However, do not forget that our ultimate goal is to perform well on previously unseen data. That problem is called generalization and will be a key focus of other chapters.
이 제한 절차는 미분 계산 calculus 과 적분 계산 integral calculus 의 기초입니다. 전자는 인수를 조작하여 함수의 값을 늘리거나 줄이는 방법을 알려줄 수 있습니다. 이는 손실 함수를 줄이기 위해 매개변수를 반복적으로 업데이트하는 딥러닝에서 직면하는 최적화 문제에 유용합니다. 최적화는 모델을 훈련 데이터에 맞추는 방법을 다루며, 미적분학은 핵심 전제 조건입니다. 그러나 우리의 궁극적인 목표는 이전에 볼 수 없었던 데이터를 잘 활용하는 것임을 잊지 마십시오. 이 문제를 일반화 generalization 라고 하며 다른 장에서 중점적으로 다룰 것입니다.
%matplotlib inline
import numpy as np
from matplotlib_inline import backend_inline
from d2l import torch as d2l
주어진 코드는 Python 코드로, Jupyter Notebook 또는 IPython 환경에서 사용됩니다. 코드는 다음과 같은 작업을 수행합니다:
- %matplotlib inline: 이 코드는 Jupyter Notebook에서 사용하는 "매직 명령어" 중 하나로, 그래프나 그림을 출력할 때 그림을 노트북 내부에 표시하도록 설정하는 역할을 합니다. 이렇게 하면 그림이 노트북 내에서 바로 볼 수 있습니다.
- import numpy as np: NumPy 라이브러리를 불러옵니다. NumPy는 파이썬의 수치 계산과 배열 처리에 유용한 라이브러리로, 주로 다차원 배열과 관련된 작업에 사용됩니다. np는 일반적으로 NumPy의 별칭으로 사용됩니다.
- from matplotlib_inline import backend_inline: matplotlib_inline 라이브러리에서 backend_inline 모듈을 가져옵니다. 이 모듈은 Matplotlib 그래프를 노트북 내에서 인라인으로 표시할 때 사용됩니다.
- from d2l import torch as d2l: D2L (Dive into Deep Learning) 라이브러리에서 torch 모듈을 가져온 다음, 이 모듈을 d2l이라는 별칭으로 사용합니다. D2L은 딥러닝 및 머신러닝 교육과 관련된 코드와 자료를 제공하는 라이브러리로, torch 모듈은 PyTorch를 기반으로 한 딥러닝 코드를 작성하기 위해 사용됩니다.
이 코드는 주로 딥러닝 및 머신러닝 관련 작업을 수행하고 시각화를 위한 환경 설정을 위해 사용됩니다. 또한 이 코드는 Jupyter Notebook 또는 IPython 환경에서 노트북 내에서 그래프 및 그림을 표시하기 위한 설정을 제공합니다.
2.4.1. Derivatives and Differentiation
Put simply, a derivative is the rate of change in a function with respect to changes in its arguments. Derivatives can tell us how rapidly a loss function would increase or decrease were we to increase or decrease each parameter by an infinitesimally small amount. Formally, for functions ƒ : ℝ → ℝ , that map from scalars to scalars, the derivative of ƒ at a point x is defined as
간단히 말해서, 도함수 derivative 는 인수의 변화에 대한 함수의 변화율입니다. Derivatives 은 각 매개변수를 극소량씩 늘리거나 줄이면 손실 함수가 얼마나 빠르게 증가하거나 감소하는지 알려줄 수 있습니다. 공식적으로, 스칼라에서 스칼라로 매핑되는 함수 f : ℝ → ℝ에 대해 점 x에서 의 도함수는 다음과 같이 정의됩니다.

lim (극한) 이란?
In mathematics, "lim" is an abbreviation for the limit. The limit is a fundamental concept in calculus and analysis that describes the behavior of a function or sequence as it approaches a certain value or approaches infinity or negative infinity.
수학에서 "lim"은 "극한(limit)"의 줄임말로 사용됩니다. 극한은 미적분학과 해석학에서 중요한 개념으로, 함수나 수열이 특정한 값을 향하거나 무한대 또는 음의 무한대를 향하는 과정을 기술합니다.
The limit of a function f(x) as x approaches a particular value, say 'a', is denoted as:
특정 값 'a'로 접근할 때 함수 f(x)의 극한은 다음과 같이 나타납니다:
lim (x → a) f(x)
This notation represents the value that the function approaches as x gets closer and closer to 'a'. In other words, it describes what happens to the function as x gets infinitely close to 'a'.
이 표기법은 x가 'a'에 점점 가까워질 때 함수가 어떻게 동작하는지를 설명합니다. 다시 말해, x가 'a'에 무한히 가까워질 때 함수가 어떻게 행동하는지를 나타냅니다.
Limits are used to study the behavior of functions, analyze continuity, and find derivatives and integrals in calculus. They are a crucial tool for understanding the fundamental properties and characteristics of functions, especially in the context of differential and integral calculus. The concept of limits is also essential in real analysis, where it is used to rigorously define continuity, convergence, and other key mathematical concepts.
극한은 미적분학에서 함수의 행동을 연구하고 연속성을 분석하며, 미분 및 적분을 찾는 데 사용되는 중요한 도구입니다. 극한은 함수의 기본적인 특성과 특징을 이해하는 데 필수적이며, 특히 미분 및 적분 미적분학의 맥락에서 중요합니다. 극한의 개념은 또한 해석학에서 사용되어 연속성, 수렴 및 기타 주요 수학적 개념을 엄밀하게 정의하는 데 필수적입니다.
This term on the right hand side is called a limit and it tells us what happens to the value of an expression as a specified variable approaches a particular value. This limit tells us what the ratio between a perturbation ℎ and the change in the function value f(x+ℎ)− f(x) converges to as we shrink its size to zero.
오른쪽에 있는 용어는 극한 limit 이라고 하며 지정된 변수가 특정 값에 접근할 때 표현식의 값에 어떤 일이 발생하는지 알려줍니다. 이 극한 limit 는 크기를 0으로 줄이면 섭동 perturbation ℎ와 함수 값 f(x+ℎ)− f(x)의 변화 사이의 비율이 수렴되는 것을 알려줍니다.
When f ′(x) exists, f is said to be differentiable at x; and when f ′(x) exists for all x on a set, e.g., the interval [a,b], we say that f is differentiable on this set. Not all functions are differentiable, including many that we wish to optimize, such as accuracy and the area under the receiving operating characteristic (AUC). However, because computing the derivative of the loss is a crucial step in nearly all algorithms for training deep neural networks, we often optimize a differentiable surrogate instead.
f ′(x)가 존재할 때 f는 x에서 미분 가능하다고 합니다. 그리고 f ′(x)가 세트의 모든 x에 대해 존재할 때(예: 구간 [a,b]), 우리는 f가 이 세트에서 미분 가능하다고 말합니다. 정확도, 수신 작동 특성(AUC) 하의 영역 등 최적화하려는 많은 기능을 포함하여 모든 기능이 차별화 가능한 것은 아닙니다. 그러나 손실의 도함수 derivative 를 계산하는 것은 심층 신경망 훈련을 위한 거의 모든 알고리즘에서 중요한 단계이기 때문에 대신 미분 가능한 대리자를 최적화하는 경우가 많습니다.
We can interpret the derivative f ′(x) as the instantaneous rate of change of f(x) with respect to x. Let’s develop some intuition with an example. Define u= f(x)=3x**2 − 4x.
도함수 f'(x)를 x에 대한 f(x)의 순간 변화율로 해석할 수 있습니다. 예를 들어 직관력을 키워 봅시다. u= f(x)=3x**2−4x를 정의합니다.
def f(x):
return 3 * x ** 2 - 4 * x주어진 코드는 파이썬에서 정의한 함수를 설명하고 있습니다. 함수 이름은 f이며, 주어진 입력(x)에 대한 출력을 계산하는 방법을 정의합니다. 함수의 내용은 다음과 같이 나타납니다:
이 코드의 설명은 다음과 같습니다:
- def f(x):: def 키워드는 파이썬 함수를 정의하기 위해 사용되며, 함수 이름인 f를 정의합니다. 괄호 안에 있는 x는 함수의 입력 매개변수(parameter)입니다. 이 함수는 x라는 입력을 받아서 계산을 수행하고 결과를 반환합니다.
- return 3 * x ** 2 - 4 * x: 이 줄은 함수의 본문(body)을 정의합니다. 주어진 x를 사용하여 함수가 수행할 계산을 기술합니다. 여기서는 입력 x를 이용하여 다음의 계산을 수행합니다:
- x를 제곱한 후 3을 곱하고,
- x를 4 곱한 다음 뺍니다.
이 함수는 주어진 x 값에 대한 결과를 반환합니다. 예를 들어, f(2)를 호출하면 x에 2를 대입하여 3 * 2 ** 2 - 4 * 2를 계산하고, 결과로 -4를 반환할 것입니다.
이 함수를 사용하면 주어진 입력값 x에 대한 함수의 출력을 계산할 수 있으며, 이러한 함수 정의는 미적분 및 수학적 모델링과 같은 다양한 수학적 응용 분야에서 사용됩니다.
Setting x=1, we see that f(x+ℎ)− f(x)/ℎ approaches 2 as ℎ approaches 0. While this experiment lacks the rigor of a mathematical proof, we can quickly see that indeed f′(1)=2.
x=1로 설정하면 ℎ가 0에 가까워짐에 따라 f(x+ℎ)− f(x)/ℎ도 2에 가까워지는 것을 알 수 있습니다. 이 실험에는 수학적 증명의 엄격함이 부족하지만, 우리는 실제로 'f′(1)=2'라는 것을 빨리 알 수 있습니다.
for h in 10.0**np.arange(-1, -6, -1):
print(f'h={h:.5f}, numerical limit={(f(1+h)-f(1))/h:.5f}')주어진 코드는 파이썬의 반복문을 사용하여 함수 f(x)의 수치 미분(numerical derivative)을 계산하고 출력하는 작업을 수행합니다. 코드는 h 값의 범위를 설정하고, 각 h에 대해 f(x) 함수의 미분 값을 계산하고 출력합니다. 아래는 코드의 설명입니다:
- for h in 10.0**np.arange(-1, -6, -1): 이 줄은 h라는 변수를 사용하여 반복을 설정합니다. np.arange(-1, -6, -1)는 -1에서 -6까지 1씩 감소하는 수열을 생성합니다. 그리고 10.0**를 사용하여 각 수열의 값에 10의 지수를 적용하여 h 값을 생성합니다. 이렇게 함으로써 h는 0.1, 0.01, 0.001, 0.0001, 0.00001의 값을 순서대로 가지게 됩니다.
- print(f'h={h:.5f}, numerical limit={(f(1+h)-f(1))/h:.5f}'): 이 줄은 각 h 값에 대한 미분 값을 계산하고 출력합니다.
- h={h:.5f}: h의 값을 소수 다섯 번째 자리까지 출력합니다.
- numerical limit={(f(1+h)-f(1))/h:.5f}: f(1+h)에서 f(1)을 뺀 다음 h로 나눈 값을 소수 다섯 번째 자리까지 출력합니다. 이 값은 f(x) 함수의 수치 미분을 나타내며, h 값이 작을수록 정확한 미분 값을 얻을 수 있습니다.
따라서 이 코드는 서로 다른 h 값에 대해 f(x) 함수의 수치 미분 값을 계산하고 출력하여, h 값이 작아질수록 정확한 미분 값을 얻는 과정을 보여줍니다. 이러한 과정은 미분 근사를 이해하고 미분 값을 추정하는 데 사용됩니다.
h=0.10000, numerical limit=2.30000
h=0.01000, numerical limit=2.03000
h=0.00100, numerical limit=2.00300
h=0.00010, numerical limit=2.00030
h=0.00001, numerical limit=2.00003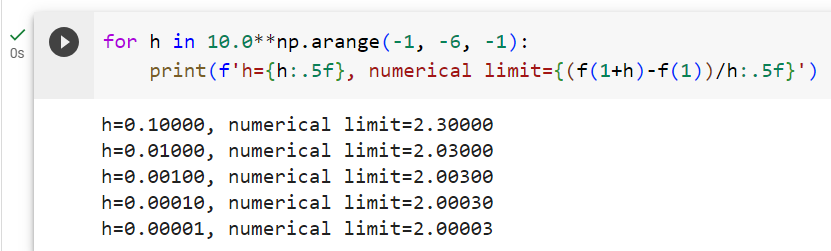
There are several equivalent notational conventions for derivatives. Given y=f(x), the following expressions are equivalent:
derivatives 에 대한 몇 가지 동등한 표기 규칙이 있습니다. y=f(x)라고 가정하면 다음 표현식은 동일합니다.
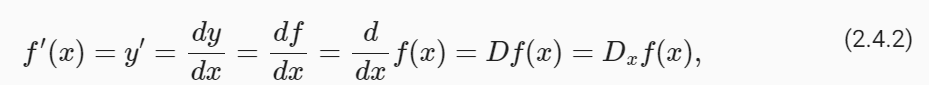
where the symbols d/dx and D are differentiation operators. Below, we present the derivatives of some common functions:
여기서 기호 d/dx와 D는 미분 연산자 differentiation operators 입니다. 아래에서는 몇 가지 일반적인 함수의 derivatives 을 제시합니다.

Functions composed from differentiable functions are often themselves differentiable. The following rules come in handy for working with compositions of any differentiable functions f and g, and constant C.
미분 가능한 함수로 구성된 함수는 종종 그 자체로 미분 가능합니다. 다음 규칙은 미분 가능한 함수 f와 g 및 상수 C의 구성 작업에 유용합니다.

Using this, we can apply the rules to find the derivative of 3x**2 − 4x via
이를 사용하여 다음을 통해 3x**2 − 4x의 도함수를 찾는 규칙을 적용할 수 있습니다.
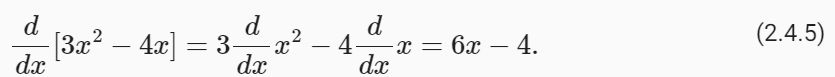
Plugging in x=1 shows that, indeed, the derivative equals 2 at this location. Note that derivatives tell us the slope of a function at a particular location.
x=1을 대입하면 실제로 이 위치에서 도함수는 2와 같다는 것을 알 수 있습니다. 도함수 derivatives 는 특정 위치에서 함수의 기울기를 알려줍니다.
2.4.2. Visualization Utilities
We can visualize the slopes of functions using the matplotlib library. We need to define a few functions. As its name indicates, use_svg_display tells matplotlib to output graphics in SVG format for crisper images. The comment #@save is a special modifier that allows us to save any function, class, or other code block to the d2l package so that we can invoke it later without repeating the code, e.g., via d2l.use_svg_display().
matplotlib 라이브러리를 사용하여 함수의 기울기를 시각화할 수 있습니다. 몇 가지 함수를 정의해야 합니다. 이름에서 알 수 있듯이 use_svg_display는 matplotlib에게 보다 선명한 이미지를 위해 SVG 형식으로 그래픽을 출력하도록 지시합니다. #@save 주석은 함수, 클래스 또는 기타 코드 블록을 d2l 패키지에 저장하여 나중에 코드를 반복하지 않고(예: d2l.use_svg_display()를 통해) 호출할 수 있도록 하는 특수 수정자 special modifier 입니다.
def use_svg_display(): #@save
"""Use the svg format to display a plot in Jupyter."""
backend_inline.set_matplotlib_formats('svg')주어진 코드는 Jupyter Notebook 환경에서 그래프나 그림을 SVG(Scalable Vector Graphics) 형식으로 표시하는 함수를 정의하는 파이썬 코드입니다. 아래는 코드의 설명입니다:
- def use_svg_display():: 이 코드는 use_svg_display라는 이름의 함수를 정의합니다. 이 함수는 그래프나 그림을 SVG 형식으로 표시하도록 설정하는 역할을 합니다.
- backend_inline.set_matplotlib_formats('svg'): 이 함수 내에서는 backend_inline 라이브러리의 set_matplotlib_formats 함수를 호출합니다. 이 함수는 Matplotlib 그래프의 출력 형식을 설정하는 역할을 합니다. 여기서 'svg'를 사용하여 SVG 형식으로 그래프를 설정합니다. SVG 형식은 확대하더라도 이미지가 깨지지 않고 고품질로 표시되며, Jupyter Notebook 환경에서 렌더링할 때 특히 유용합니다.
따라서 이 코드는 Jupyter Notebook 환경에서 그래프를 그릴 때 그래프의 형식을 SVG로 설정하여, 그래프가 화면에 고해상도로 표시되도록 하는 함수를 정의하고 있습니다. 이 함수를 사용하면 Jupyter Notebook에서 품질 좋은 그래프를 생성하고 시각화할 때 유용합니다.
Conveniently, we can set figure sizes with set_figsize. Since the import statement from matplotlib import pyplot as plt was marked via #@save in the d2l package, we can call d2l.plt.
편리하게도 set_figsize를 사용하여 그림 크기를 설정할 수 있습니다. matplotlib import pyplot as plt의 import 문이 d2l 패키지의 #@save를 통해 표시되었으므로 d2l.plt를 호출할 수 있습니다.
def set_figsize(figsize=(3.5, 2.5)): #@save
"""Set the figure size for matplotlib."""
use_svg_display()
d2l.plt.rcParams['figure.figsize'] = figsize주어진 코드는 Matplotlib를 사용하여 그림의 크기를 설정하는 함수를 정의하는 파이썬 코드입니다. 아래는 코드의 설명입니다:
- def set_figsize(figsize=(3.5, 2.5)):: 이 코드는 set_figsize라는 이름의 함수를 정의합니다. 이 함수는 그림의 크기를 설정하는 역할을 합니다. figsize 매개변수를 사용하여 원하는 그림 크기를 지정할 수 있으며, 기본값은 (3.5, 2.5)로 설정되어 있습니다.
- use_svg_display(): use_svg_display 함수를 호출하여 그래프를 SVG 형식으로 표시하도록 설정합니다. 이전 질문에 설명한 대로, SVG 형식은 고품질 그래프를 표시하는 데 유용합니다.
- d2l.plt.rcParams['figure.figsize'] = figsize: Matplotlib의 rcParams를 사용하여 그림의 크기를 설정합니다. figsize 매개변수에 지정된 크기로 그림을 설정합니다. 이것은 Matplotlib 그래프의 기본 크기를 변경하는 것으로, figsize를 통해 그림의 가로와 세로 크기를 지정할 수 있습니다.
따라서 이 코드는 Matplotlib를 사용하여 그림의 크기를 설정하는 함수를 정의하고 있으며, 그림 크기를 사용자 지정하거나 기본 설정을 변경하는 데 사용됩니다. 이를 통해 생성되는 그림은 원하는 크기로 표시되며, 시각화 결과를 조절할 수 있습니다.
The set_axes function can associate axes with properties, including labels, ranges, and scales.
set_axes 함수는 축을 레이블, 범위, 스케일 등의 속성과 연결할 수 있습니다.
#@save
def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):
"""Set the axes for matplotlib."""
axes.set_xlabel(xlabel), axes.set_ylabel(ylabel)
axes.set_xscale(xscale), axes.set_yscale(yscale)
axes.set_xlim(xlim), axes.set_ylim(ylim)
if legend:
axes.legend(legend)
axes.grid()주어진 코드는 Matplotlib 그래프의 축(axis) 설정을 수행하는 함수를 설명하는 파이썬 코드입니다. 이 함수를 사용하면 그래프의 축 레이블, 범위, 스케일, 범례, 그리드 등을 설정할 수 있습니다. 아래는 코드의 설명입니다:
- def set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend):: 이 코드는 set_axes라는 이름의 함수를 정의합니다. 이 함수는 Matplotlib 그래프의 축 설정을 담당합니다. 함수는 다음과 같은 매개변수를 사용합니다:
- axes: 설정할 축(axis) 객체.
- xlabel: x-축 레이블.
- ylabel: y-축 레이블.
- xlim: x-축 범위.
- ylim: y-축 범위.
- xscale: x-축 스케일.
- yscale: y-축 스케일.
- legend: 범례 설정.
- axes.set_xlabel(xlabel), axes.set_ylabel(ylabel): x-축과 y-축의 레이블을 설정합니다.
- axes.set_xscale(xscale), axes.set_yscale(yscale): x-축과 y-축의 스케일을 설정합니다. 스케일은 "linear" 또는 "log"와 같은 값으로 설정할 수 있으며, 스케일을 변경하면 축의 데이터 표시 방식이 변경됩니다.
- axes.set_xlim(xlim), axes.set_ylim(ylim): x-축과 y-축의 범위를 설정합니다. 범위는 그래프에서 보여질 데이터의 최솟값과 최댓값을 지정합니다.
- if legend: axes.legend(legend): 만약 legend 매개변수가 주어지면 그래프에 범례를 추가합니다. 범례는 그래프에서 각 선 또는 데이터 시리즈를 설명하는 레이블을 표시하는 데 사용됩니다.
- axes.grid(): 그리드를 추가하여 그래프에 격자 눈금을 표시합니다. 격자 눈금은 데이터의 위치를 더 쉽게 파악할 수 있도록 도와줍니다.
이 함수를 사용하면 Matplotlib 그래프의 축을 사용자 정의하고, 그래프를 보다 명확하게 표시하는 데 도움이 됩니다.
With these three functions, we can define a plot function to overlay multiple curves. Much of the code here is just ensuring that the sizes and shapes of inputs match.
이 세 가지 함수를 사용하면 여러 곡선을 오버레이하는 플롯 함수를 정의할 수 있습니다. 여기 코드의 대부분은 입력의 크기와 모양이 일치하는지 확인하는 것입니다.
#@save
def plot(X, Y=None, xlabel=None, ylabel=None, legend=[], xlim=None,
ylim=None, xscale='linear', yscale='linear',
fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None):
"""Plot data points."""
def has_one_axis(X): # True if X (tensor or list) has 1 axis
return (hasattr(X, "ndim") and X.ndim == 1 or isinstance(X, list)
and not hasattr(X[0], "__len__"))
if has_one_axis(X): X = [X]
if Y is None:
X, Y = [[]] * len(X), X
elif has_one_axis(Y):
Y = [Y]
if len(X) != len(Y):
X = X * len(Y)
set_figsize(figsize)
if axes is None:
axes = d2l.plt.gca()
axes.cla()
for x, y, fmt in zip(X, Y, fmts):
axes.plot(x,y,fmt) if len(x) else axes.plot(y,fmt)
set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend)주어진 코드는 데이터 포인트를 그리는 함수를 설명하는 파이썬 코드입니다. 이 함수를 사용하면 데이터 포인트를 그래프로 표시할 수 있으며, 그래프의 모양, 축, 범위, 스케일, 범례, 그리드 등을 설정할 수 있습니다. 아래는 코드의 설명입니다:
- plot(X, Y=None, xlabel=None, ylabel=None, legend=[], xlim=None, ylim=None, xscale='linear', yscale='linear', fmts=('-', 'm--', 'g-.', 'r:'), figsize=(3.5, 2.5), axes=None): 이 함수는 데이터 포인트를 그리는 함수로, 다양한 설정 옵션을 제공합니다. 이 함수는 다음과 같은 매개변수를 사용합니다:
- X: x-축에 대한 데이터 포인트 또는 데이터 포인트 리스트.
- Y: y-축에 대한 데이터 포인트 또는 데이터 포인트 리스트. 기본값은 None이며, 이 경우 X가 y-축 데이터로 사용됩니다.
- xlabel: x-축 레이블.
- ylabel: y-축 레이블.
- legend: 범례 설정. 여러 데이터 시리즈에 대한 범례를 지정할 수 있습니다.
- xlim: x-축 범위 설정.
- ylim: y-축 범위 설정.
- xscale: x-축 스케일 설정. 기본값은 "linear"로 설정되어 있습니다.
- yscale: y-축 스케일 설정. 기본값은 "linear"로 설정되어 있습니다.
- fmts: 그래프의 스타일 설정. 여러 다른 선 스타일을 제공하며, 기본값은 ('-', 'm--', 'g-.', 'r:')로 설정되어 있습니다.
- figsize: 그래프의 크기 설정. 기본값은 (3.5, 2.5)로 설정되어 있습니다.
- axes: 그래프를 그릴 Matplotlib 축 객체. 기본값은 None으로 설정되어 있으며, 필요한 경우 사용자가 직접 설정할 수 있습니다.
- def has_one_axis(X): 이 내부 함수는 주어진 데이터(X)가 1차원 배열 또는 리스트인지 확인합니다. 1차원이면 True를 반환하고, 그렇지 않으면 False를 반환합니다.
- if has_one_axis(X): X = [X]: 만약 X가 1차원 배열이라면, X를 원소가 하나인 리스트로 변환합니다. 이렇게 함으로써 여러 데이터 시리즈를 다룰 때 편리하게 처리할 수 있습니다.
- if Y is None: X, Y = [[]] * len(X), X: 만약 Y가 주어지지 않았다면, X를 y-축 데이터로 사용하기 위해 Y를 X로 설정합니다. 그리고 X를 원소가 비어 있는 리스트로 설정합니다.
- set_figsize(figsize): 그래프의 크기를 figsize에 지정된 크기로 설정하는 함수를 호출합니다.
- if axes is None: axes = d2l.plt.gca(): 만약 축(axes)가 주어지지 않았다면, 현재 활성화된 Matplotlib 축 객체를 가져와서 사용합니다.
- axes.cla(): 축 객체를 초기화하여 이전에 그려진 그래프를 지우고 새로운 그래프를 그릴 준비를 합니다.
- for x, y, fmt in zip(X, Y, fmts): axes.plot(x, y, fmt) if len(x) else axes.plot(y, fmt): X와 Y에 대한 데이터 시리즈와 스타일(fmt)을 순회하면서 그래프를 그립니다. 만약 x 데이터 시리즈가 비어 있다면(len(x) == 0), y 데이터 시리즈를 그래프로 그립니다.
- set_axes(axes, xlabel, ylabel, xlim, ylim, xscale, yscale, legend): set_axes 함수를 호출하여 축의 레이블, 범위, 스케일, 범례, 그리드 등을 설정합니다.
이 함수를 사용하면 주어진 데이터 포인트를 그래프로 시각화하고, 그래프의 모양과 설정을 유연하게 조절할 수 있습니다. 이는 데이터 시각화 및 그래프 생성에 유용한 도구입니다.
Now we can plot the function u=f(x) and its tangent line y=2x−3 at x=1, where the coefficient 2 is the slope of the tangent line.
이제 x=1에서 함수 u=f(x)와 접선 y=2x−3을 그릴 수 있습니다. 여기서 계수 2는 접선의 기울기입니다.
x = np.arange(0, 3, 0.1)
plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])주어진 코드는 주어진 범위에서 함수 f(x)와 x=1에서의 접선을 그래프로 표시하는 예제 코드입니다. 아래는 코드의 설명입니다:
- x = np.arange(0, 3, 0.1): 이 코드는 0에서 3까지의 범위에서 0.1 간격으로 숫자를 생성하여 x에 할당합니다. 이렇게 생성된 x 값은 함수 f(x)와 접선을 그래프로 그릴 때 x-축 값으로 사용됩니다.
- plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)']): plot 함수를 호출하여 그래프를 그립니다. 이때, 다음 매개변수들이 사용됩니다:
- x: x-축 데이터로 사용될 범위(0에서 3까지의 값).
- [f(x), 2 * x - 3]: y-축 데이터로 사용될 값. 여기서 f(x)는 함수 f(x)의 값이고, 2 * x - 3은 x=1에서의 접선의 방정식입니다.
- 'x': x-축 레이블로 사용될 문자열.
- 'f(x)': y-축 레이블로 사용될 문자열.
- legend=['f(x)', 'Tangent line (x=1)']: 범례 설정으로, 각 데이터 시리즈에 대한 설명을 제공합니다.
이 코드는 x 범위에서 f(x) 함수와 x=1에서의 접선을 그래프로 그립니다. 이를 통해 함수와 해당 지점에서의 기울기를 시각화할 수 있습니다.

2.4.3. Partial Derivatives and Gradients
Thus far, we have been differentiating functions of just one variable. In deep learning, we also need to work with functions of many variables. We briefly introduce notions of the derivative that apply to such multivariate functions.
지금까지 우리는 단 하나의 변수에 대한 함수를 차별화해 왔습니다. 딥러닝에서는 다양한 변수의 함수를 다루어야 합니다. 우리는 그러한 다변량 함수에 적용되는 미분의 개념을 간략하게 소개합니다.
Let y=f(x1,x2,…,xn) be a function with n variables. The partial derivative of y with respect to its i th parameter xi is
y=f(x1,x2,…,xn)을 n개의 변수를 갖는 함수로 둡니다. i 번째 매개변수 xi에 대한 y의 편도함수 multivariate functions는 다음과 같습니다.

To calculate ∂y/ ∂xi, we can treat x1,…,xi−1,xi+1,…,xn as constants and calculate the derivative of y with respect to xi. The following notational conventions for partial derivatives are all common and all mean the same thing:
∂y/ ∂xi를 계산하려면 x1,…,xi−1,xi+1,…,xn을 상수로 처리하고 xi에 대한 y의 도함수를 계산할 수 있습니다. 부분 도함수에 대한 다음 표기 규칙은 모두 공통적이며 모두 같은 의미입니다.

We can concatenate partial derivatives of a multivariate function with respect to all its variables to obtain a vector that is called the gradient of the function. Suppose that the input of function f: ℝ**n→ ℝ is an n-dimensional vector x=[x1,x2,…,xn]**⊤ and the output is a scalar. The gradient of the function f with respect to x is a vector of n partial derivatives:
모든 변수에 대해 다변량 함수의 부분 도함수를 연결하여 함수의 기울기라고 하는 벡터를 얻을 수 있습니다. 함수 f: ℝ**n→ ℝ의 입력이 n차원 벡터 x=[x1,x2,…,xn]**⊤이고 출력이 스칼라라고 가정합니다. x에 대한 함수 f의 기울기는 n 편도함수의 벡터입니다.

When there is no ambiguity, ∇xf(x) is typically replaced by ∇f(x). The following rules come in handy for differentiating multivariate functions:
모호성 ambiguity 이 없으면 ∇xf(x)는 일반적으로 ∇f(x)로 대체됩니다. 다변량 함수를 차별화하는 데 다음 규칙이 유용합니다.
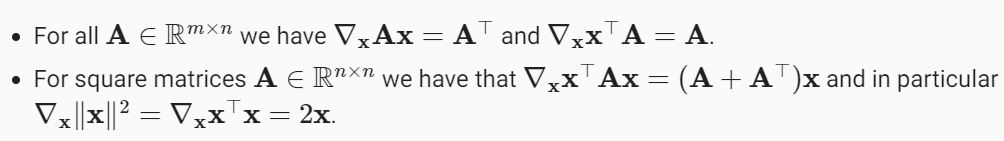
Similarly, for any matrix X, we have ∇x|X|2F=2X.
마찬가지로, 임의의 행렬 X에 대해 ∇x|X|2F=2X가 됩니다.
2.4.4. Chain Rule
In deep learning, the gradients of concern are often difficult to calculate because we are working with deeply nested functions (of functions (of functions…)). Fortunately, the chain rule takes care of this. Returning to functions of a single variable, suppose that y=f(g(x)) and that the underlying functions y=f(u) and u=g(x) are both differentiable. The chain rule states that
딥 러닝에서는 깊게 중첩된 함수(함수 중(함수…))로 작업하기 때문에 관심 기울기를 계산하기 어려운 경우가 많습니다. 다행히도 체인 규칙이 이를 처리합니다. 단일 변수의 함수로 돌아가서, y=f(g(x))와 기본 함수 y=f(u) 및 u=g(x)가 모두 미분 가능하다고 가정합니다. 체인 규칙은 다음과 같이 명시합니다.

Turning back to multivariate functions, suppose that y=f(u) has variables u1,u2,…,un, where each ui=gi(X) has variables x1,x2,…,xn, i.e., u=g(x). Then the chain rule states that
다변량 함수로 돌아가서, y=f(u)에 변수 u1,u2,…,un이 있다고 가정합니다. 여기서 각 ui=gi(X)에는 변수 x1,x2,…,xn이 있습니다. 즉, u=g(x) . 그런 다음 체인 규칙은 다음과 같이 명시합니다.
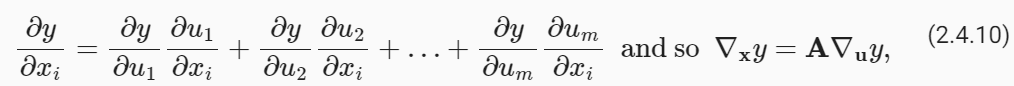
where A∈ ℝ n×m is a matrix that contains the derivative of vector u with respect to vector x. Thus, evaluating the gradient requires computing a vector–matrix product. This is one of the key reasons why linear algebra is such an integral building block in building deep learning systems.
여기서 A∈ ℝn×m은 벡터 x에 대한 벡터 u의 도함수를 포함하는 행렬입니다. 따라서 기울기를 평가하려면 벡터-행렬 곱을 계산해야 합니다. 이것이 선형 대수학이 딥 러닝 시스템을 구축하는 데 필수적인 구성 요소인 주요 이유 중 하나입니다.
2.4.5. Discussion
While we have just scratched the surface of a deep topic, a number of concepts already come into focus: first, the composition rules for differentiation can be applied routinely, enabling us to compute gradients automatically. This task requires no creativity and thus we can focus our cognitive powers elsewhere. Second, computing the derivatives of vector-valued functions requires us to multiply matrices as we trace the dependency graph of variables from output to input. In particular, this graph is traversed in a forward direction when we evaluate a function and in a backwards direction when we compute gradients. Later chapters will formally introduce backpropagation, a computational procedure for applying the chain rule.
우리는 단지 깊은 주제의 표면만 긁었을 뿐이지만 이미 여러 가지 개념에 초점을 맞추고 있습니다. 첫째, 미분을 위한 합성 규칙을 일상적으로 적용하여 기울기를 자동으로 계산할 수 있습니다. 이 작업에는 창의성이 필요하지 않으므로 인지 능력을 다른 곳에 집중할 수 있습니다. 둘째, 벡터 값 함수의 도함수를 계산하려면 출력에서 입력까지 변수의 종속성 그래프를 추적하면서 행렬을 곱해야 합니다. 특히, 이 그래프는 함수를 평가할 때 정방향으로 이동하고 기울기를 계산할 때 역방향으로 이동합니다. 이후 장에서는 체인 규칙을 적용하기 위한 계산 절차인 역전파를 공식적으로 소개할 것입니다.
From the viewpoint of optimization, gradients allow us to determine how to move the parameters of a model in order to lower the loss, and each step of the optimization algorithms used throughout this book will require calculating the gradient.
최적화 관점에서 기울기를 사용하면 손실을 낮추기 위해 모델의 매개변수를 이동하는 방법을 결정할 수 있으며, 이 책 전체에서 사용되는 최적화 알고리즘의 각 단계에서는 기울기 계산이 필요합니다.
2.4.6. Exercises

'Dive into Deep Learning > D2L Preliminaries' 카테고리의 다른 글
| D2L - 2.7. Documentation (2) | 2023.10.14 |
|---|---|
| D2L - 2.6. Probability and Statistics (0) | 2023.10.14 |
| D2L - 2.5. Automatic Differentiation (0) | 2023.10.12 |
| D2L - 2.3. Linear Algebra - 선형 대수학 (1) | 2023.10.11 |
| D2L - 2.2. Data Preprocessing (0) | 2023.10.09 |
| D2L - 2.1. Data Manipulation (0) | 2023.10.09 |
| D2L - 2. Preliminaries (0) | 2023.10.09 |

