15.5. Word Embedding with Global Vectors (GloVe) — Dive into Deep Learning 1.0.3 documentation
d2l.ai
15.5. Word Embedding with Global Vectors (GloVe)
Word-word co-occurrences within context windows may carry rich semantic information. For example, in a large corpus word “solid” is more likely to co-occur with “ice” than “steam”, but word “gas” probably co-occurs with “steam” more frequently than “ice”. Besides, global corpus statistics of such co-occurrences can be precomputed: this can lead to more efficient training. To leverage statistical information in the entire corpus for word embedding, let’s first revisit the skip-gram model in Section 15.1.3, but interpreting it using global corpus statistics such as co-occurrence counts.
15.1. Word Embedding (word2vec) — Dive into Deep Learning 1.0.3 documentation
d2l.ai
컨텍스트 창 내에서 단어-단어 동시 발생 Word-word co-occurrences 은 풍부한 의미 정보를 전달할 수 있습니다. 예를 들어, 대규모 코퍼스에서 "solid"라는 단어는 "steam"보다 "ice"와 함께 나타날 가능성이 더 높지만 "gas"라는 단어는 "ice"보다 "steam"과 더 자주 함께 나타날 가능성이 높습니다. 게다가, 그러한 동시 발생에 대한 글로벌 코퍼스 통계가 미리 계산될 수 있습니다. 이는 보다 효율적인 훈련으로 이어질 수 있습니다. 단어 임베딩을 위해 전체 코퍼스의 통계 정보를 활용하기 위해 먼저 섹션 15.1.3의 스킵 그램 모델을 다시 방문하되 동시 발생 횟수와 같은 전역 코퍼스 통계를 사용하여 해석해 보겠습니다.
15.5.1. Skip-Gram with Global Corpus Statistics
Denoting by qij the conditional probability P(wj∣wi) of word wj given word wi in the skip-gram model, we have this formula where for any index i vectors vi and ui represent word wi as the center word and context word, respectively, and V={0,1,…,|V|−1} is the index set of the vocabulary.

스킵-그램 모델에서 단어 wi가 주어졌을 때 단어 wj의 조건부 확률 P(wj∣wi)를 qij로 표시하면 다음 공식을 얻을 수 있습니다. 여기서 모든 인덱스 i에 대해 벡터 vi와 ui는 단어 wi를 각각 중심 단어와 문맥 단어로 나타냅니다. , 그리고 V={0,1,…,|V|−1}은 어휘의 인덱스 세트입니다.
Consider word wi that may occur multiple times in the corpus. In the entire corpus, all the context words wherever wi is taken as their center word form a multiset Ci of word indices that allows for multiple instances of the same element. For any element, its number of instances is called its multiplicity. To illustrate with an example, suppose that word wi occurs twice in the corpus and indices of the context words that take wi as their center word in the two context windows are k,j,m,k and k,l,k,j. Thus, multiset Ci={j,j,k,k,k,k,l,m}, where multiplicities of elements j,k,l,m are 2, 4, 1, 1, respectively.
말뭉치에서 여러 번 나타날 수 있는 단어 wi를 생각해 보세요. 전체 코퍼스에서 wi가 중심 단어로 사용되는 모든 문맥 단어는 동일한 요소의 여러 인스턴스를 허용하는 단어 인덱스의 다중 집합 Ci를 형성합니다. 모든 요소에 대해 인스턴스 수를 다중성이라고 합니다. 예를 들어 설명하자면, 단어 wi가 말뭉치에 두 번 나타나고 두 문맥 창에서 wi를 중심 단어로 하는 문맥 단어의 인덱스가 k,j,m,k 및 k,l,k,j라고 가정합니다. 따라서 다중 집합 Ci={j,j,k,k,k,k,l,m}이며, 여기서 요소 j,k,l,m의 다중도는 각각 2, 4, 1, 1입니다.
Now let’s denote the multiplicity of element j in multiset Ci as xij. This is the global co-occurrence count of word wj (as the context word) and word wi (as the center word) in the same context window in the entire corpus. Using such global corpus statistics, the loss function of the skip-gram model is equivalent to this fomular,
이제 다중집합 Ci에서 요소 j의 다중도를 xij로 표시해 보겠습니다. 이는 전체 말뭉치에서 동일한 컨텍스트 창에 있는 단어 wj(문맥 단어)와 단어 wi(중앙 단어)의 전역 동시 발생 횟수입니다. 이러한 전역 코퍼스 통계를 사용하면 스킵그램 모델의 손실 함수는 다음 공식과 동일합니다.

We further denote by xi the number of all the context words in the context windows where wi occurs as their center word, which is equivalent to |Ci|. Letting pij be the conditional probability xij/ki for generating context word wj given center word wi, (15.5.2) can be rewritten as
또한 wi가 중심 단어로 나타나는 컨텍스트 창의 모든 컨텍스트 단어 수를 xi로 표시하며 이는 |Ci|와 동일합니다. pij를 중심 단어 wi가 주어졌을 때 문맥 단어 wj를 생성하기 위한 조건부 확률 xij/ki라고 하면 (15.5.2)는 다음 공식으로 다시 작성할 수 있습니다.

In (15.5.3), −∑j∈vpij**log qij calculates the cross-entropy of the conditional distribution pij of global corpus statistics and the conditional distribution qij of model predictions. This loss is also weighted by xi as explained above. Minimizing the loss function in (15.5.3) will allow the predicted conditional distribution to get close to the conditional distribution from the global corpus statistics.
(15.5.3)에서 −∑j∈vpij**log qij는 전역 코퍼스 통계의 조건부 분포 pij와 모델 예측의 조건부 분포 qij의 교차 엔트로피를 계산합니다. 이 손실은 위에서 설명한 대로 xi에 의해 가중치가 부여됩니다. (15.5.3)에서 손실함수를 최소화하면 예측된 조건부 분포가 전역 코퍼스 통계의 조건부 분포에 가까워질 수 있습니다.
Though being commonly used for measuring the distance between probability distributions, the cross-entropy loss function may not be a good choice here. On the one hand, as we mentioned in Section 15.2, the cost of properly normalizing qij results in the sum over the entire vocabulary, which can be computationally expensive. On the other hand, a large number of rare events from a large corpus are often modeled by the cross-entropy loss to be assigned with too much weight.
확률 분포 사이의 거리를 측정하는 데 일반적으로 사용되지만 교차 엔트로피 손실 함수는 여기서는 좋은 선택이 아닐 수 있습니다. 한편으로, 섹션 15.2에서 언급했듯이 qij를 적절하게 정규화하는 비용은 전체 어휘에 대한 합계를 산출하므로 계산 비용이 많이 들 수 있습니다. 반면, 대규모 코퍼스에서 발생하는 다수의 희귀 이벤트는 교차 엔트로피 손실로 모델링되어 너무 많은 가중치가 할당되는 경우가 많습니다.
15.5.2. The GloVe Model
In view of this, the GloVe model makes three changes to the skip-gram model based on squared loss (Pennington et al., 2014):
이를 고려하여 GloVe 모델은 손실 제곱을 기반으로 하는 스킵 그램 모델에 세 가지 변경 사항을 적용합니다(Pennington et al., 2014).

Putting all things together, training GloVe is to minimize the following loss function:
모든 것을 종합하면 GloVe 교육은 다음 손실 함수를 최소화하는 것입니다.

For the weight function, a suggested choice is: ℎ(x)=(x/c)**α (e.g α=0.75) if x<c (e.g., c=100); otherwise ℎ(x)=1. In this case, because ℎ(0)=0, the squared loss term for any xij=0 can be omitted for computational efficiency. For example, when using minibatch stochastic gradient descent for training, at each iteration we randomly sample a minibatch of non-zero xij to calculate gradients and update the model parameters. Note that these non-zero xij are precomputed global corpus statistics; thus, the model is called GloVe for Global Vectors.
가중치 함수의 경우 제안되는 선택은 다음과 같습니다. x<c(예: c=100)인 경우 ℎ(x)=(x/c)**α(예: α=0.75); 그렇지 않으면 ℎ(x)=1입니다. 이 경우 ℎ(0)=0이므로 xij=0에 대한 제곱 손실 항은 계산 효율성을 위해 생략될 수 있습니다. 예를 들어, 훈련을 위해 미니배치 확률적 경사하강법을 사용할 때 각 반복마다 0이 아닌 xij의 미니배치를 무작위로 샘플링하여 경사를 계산하고 모델 매개변수를 업데이트합니다. 0이 아닌 xij는 미리 계산된 글로벌 코퍼스 통계입니다. 따라서 이 모델은 전역 벡터용 GloVe라고 합니다.
It should be emphasized that if word wi appears in the context window of word wj, then vice versa. Therefore, xij=xji. Unlike word2vec that fits the asymmetric conditional probability pij, GloVe fits the symmetric logxij. Therefore, the center word vector and the context word vector of any word are mathematically equivalent in the GloVe model. However in practice, owing to different initialization values, the same word may still get different values in these two vectors after training: GloVe sums them up as the output vector.
wj라는 단어의 컨텍스트 창에 wi라는 단어가 나타나면 그 반대의 경우도 마찬가지라는 점을 강조해야 합니다. 따라서 xij=xji입니다. 비대칭 조건부 확률 pij에 맞는 word2vec와 달리 GloVe는 대칭 logxij에 적합합니다. 따라서 모든 단어의 중심 단어 벡터와 문맥 단어 벡터는 GloVe 모델에서 수학적으로 동일합니다. 그러나 실제로는 초기화 값이 다르기 때문에 동일한 단어가 훈련 후에도 두 벡터에서 서로 다른 값을 얻을 수 있습니다. GloVe는 이를 출력 벡터로 합산합니다.
15.5.3. Interpreting GloVe from the Ratio of Co-occurrence Probabilities
We can also interpret the GloVe model from another perspective. Using the same notation in Section 15.5.1, let pij =def P(wj|wi) be the conditional probability of generating the context word wj given wi as the center word in the corpus. tab_glove lists several co-occurrence probabilities given words “ice” and “steam” and their ratios based on statistics from a large corpus.
GloVe 모델을 다른 관점에서 해석할 수도 있습니다. 섹션 15.5.1의 동일한 표기법을 사용하여, pij =def P(wj|wi)를 말뭉치의 중심 단어로 wi가 주어진 문맥 단어 wj를 생성하는 조건부 확률로 둡니다. tab_glove는 "ice"와 "steam"이라는 단어가 주어진 여러 동시 발생 확률과 대규모 코퍼스의 통계를 기반으로 한 비율을 나열합니다.
:Word-word co-occurrence probabilities and their ratios from a large corpus (adapted from Table 1 in Pennington et al. (2014))
: 대규모 자료의 단어-단어 동시 발생 확률 및 그 비율(Pennington et al.(2014)의 표 1에서 채택)
Table 15.5.1 label:tab_glove
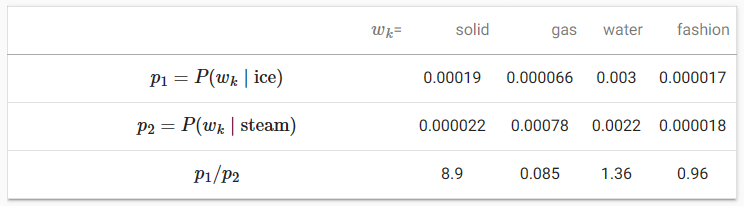
We can observe the following from tab_glove:
tab_glove에서 다음을 관찰할 수 있습니다.
- For a word wk that is related to “ice” but unrelated to “steam”, such as wk=solid, we expect a larger ratio of co-occurence probabilities, such as 8.9.
- wk=solid와 같이 “ice”와 관련이 있지만 “steam”과 관련이 없는 단어 wk의 경우 8.9와 같이 더 큰 동시 발생 확률 비율이 예상됩니다.
- For a word wk that is related to “steam” but unrelated to “ice”, such as wk=gas, we expect a smaller ratio of co-occurence probabilities, such as 0.085.
- wk=gas와 같이 "증기"와 관련이 있지만 "얼음"과 관련이 없는 단어 wk의 경우 0.085와 같이 더 작은 동시 발생 확률 비율이 예상됩니다.
- For a word wk that is related to both “ice” and “steam”, such as wk=water, we expect a ratio of co-occurence probabilities that is close to 1, such as 1.36.
- wk=물과 같이 "얼음"과 "증기" 모두와 관련된 단어 wk의 경우 1.36과 같이 1에 가까운 동시 발생 확률 비율을 예상합니다.
- For a word wk that is unrelated to both “ice” and “steam”, such as wk=fashion, we expect a ratio of co-occurence probabilities that is close to 1, such as 0.96.
- wk=fashion과 같이 "ice"와 "steam" 모두와 관련이 없는 단어 wk의 경우 0.96과 같이 1에 가까운 동시 발생 확률 비율을 기대합니다.
It can be seen that the ratio of co-occurrence probabilities can intuitively express the relationship between words. Thus, we can design a function of three word vectors to fit this ratio. For the ratio of co-occurrence probabilities pij/pik with wi being the center word and wj and wk being the context words, we want to fit this ratio using some function f:
동시발생 확률의 비율을 통해 단어 간의 관계를 직관적으로 표현할 수 있음을 알 수 있다. 따라서 우리는 이 비율에 맞게 세 단어 벡터의 함수를 설계할 수 있습니다. wi가 중심 단어이고 wj와 wk가 문맥 단어인 동시 발생 확률 pij/pik의 비율에 대해 우리는 일부 함수 f를 사용하여 이 비율을 맞추고 싶습니다.

Among many possible designs for f, we only pick a reasonable choice in the following. Since the ratio of co-occurrence probabilities is a scalar, we require that f be a scalar function, such as f(uj,uk,vi)=f((ui−uk)**⊤vi). Switching word indices j and k in (15.5.5), it must hold that f(x)f(−x)=1, so one possibility is f(x)=exp(x), i.e.,
f에 대해 가능한 많은 디자인 중에서 우리는 다음 중에서 합리적인 선택만을 선택합니다. 동시 발생 확률의 비율은 스칼라이므로 f는 f(uj,uk,vi)=f((ui−uk)**⊤vi)와 같은 스칼라 함수여야 합니다. (15.5.5)에서 단어 인덱스 j와 k를 전환하면 f(x)f(−x)=1을 유지해야 하므로 한 가지 가능성은 f(x)=exp(x)입니다. 즉,

Now let’s pick exp(uj**⊤ vi)≈αpij, where α is a constant. Since pij=xij/xi, after taking the logarithm on both sides we get uj**⊤ vi≈log α+log xij − log xi. We may use additional bias terms to fit −log α + log xi, such as the center word bias bi and the context word bias cj:
이제 α가 상수인 exp(uj**⊤ vi)αpij를 선택해 보겠습니다. pij=xij/xi이므로, 양쪽에 로그를 취한 후 uj**⊤ vi≒log α+log xij − log xi를 얻습니다. 중심 단어 바이어스 bi 및 문맥 단어 바이어스 cj와 같이 −log α + log xi를 맞추기 위해 추가 바이어스 항을 사용할 수 있습니다.

Measuring the squared error of (15.5.7) with weights, the GloVe loss function in (15.5.4) is obtained.
가중치를 사용하여 (15.5.7)의 제곱 오차를 측정하면 (15.5.4)의 GloVe 손실 함수가 얻어집니다.
GloVe Model 이란?
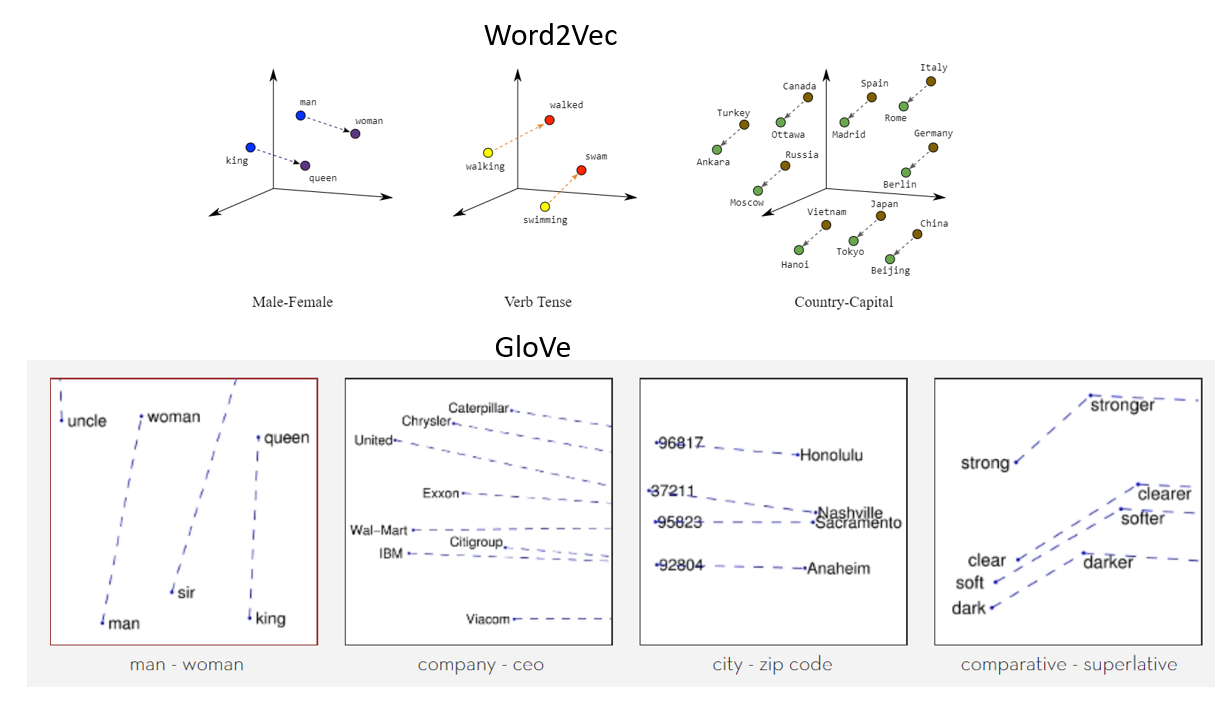
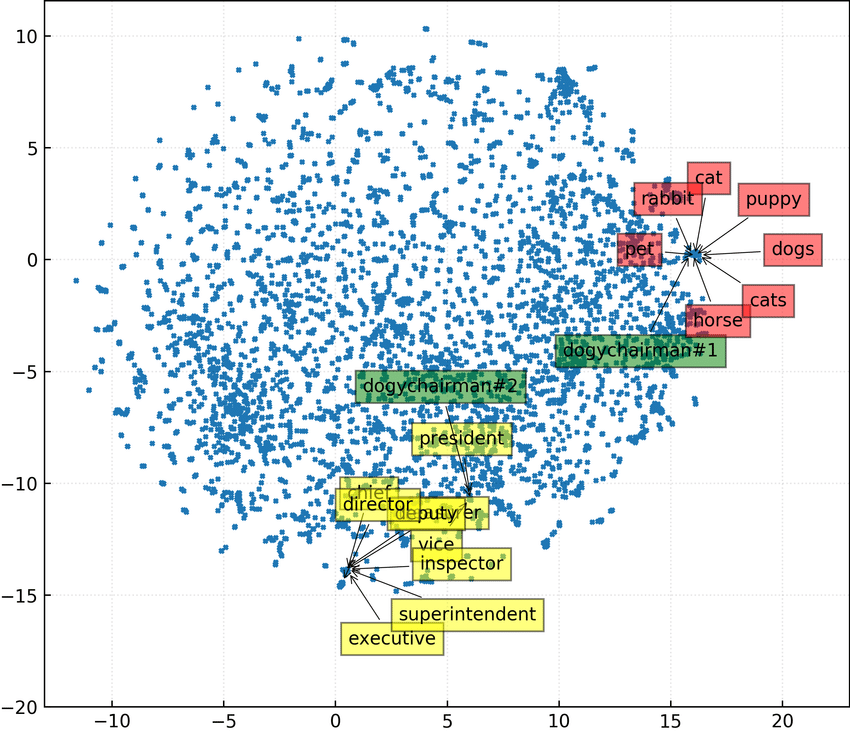
The GloVe model, short for Global Vectors for Word Representation, is an unsupervised learning algorithm designed to create word embeddings – numerical representations of words – from large text corpora. These word embeddings capture semantic relationships between words and are used in various natural language processing (NLP) tasks.
GloVe 모델은 Global Vectors for Word Representation의 약자로, 대용량 텍스트 말뭉치에서 단어 임베딩 – 단어의 숫자 표현 – 을 생성하기 위한 비지도 학습 알고리즘입니다. 이러한 단어 임베딩은 단어 간 의미 관계를 포착하며 다양한 자연어 처리 (NLP) 작업에서 사용됩니다.
The key idea behind the GloVe model is to factorize the word co-occurrence matrix, which represents how often words appear together in a given context window. By analyzing these co-occurrence statistics, GloVe learns to embed words in a continuous vector space where similar words are closer to each other, and relationships between words are preserved.
GloVe 모델의 핵심 아이디어는 word co-occurrence matrix을 분해하는 것입니다. 이 행렬은 주어진 문맥 창 내에서 단어가 얼마나 자주 함께 나타나는지를 나타냅니다. 이러한 공기 발생 통계를 분석하여 GloVe는 유사한 단어가 서로 가까이 위치하고 단어 간 관계가 보존되는 연속 벡터 공간에 단어를 임베딩하는 방법을 학습합니다.
Here's a brief overview of how the GloVe model works:
다음은 GloVe 모델의 작동 방식에 대한 간략한 개요입니다:
- Construct the Co-occurrence Matrix: Create a co-occurrence matrix that counts how often each word appears in the context of other words within a specified window.
공기 발생 행렬 생성: 지정된 창 내에서 각 단어가 다른 단어와 함께 나타나는 빈도를 계산하는 공기 발생 행렬을 생성합니다. - Initialize Word Vectors: Initialize word vectors randomly for each word.
단어 벡터 초기화: 각 단어에 대해 단어 벡터를 무작위로 초기화합니다. - Define the GloVe Objective Function: Define an objective function that measures the difference between the dot product of word vectors and the logarithm of the co-occurrence probabilities. The aim is to minimize the difference.
GloVe 목적 함수 정의: 단어 벡터의 내적과 공기 발생 확률의 로그 차이를 측정하는 목적 함수를 정의합니다. 목표는 차이를 최소화하는 것입니다. - Optimize the Objective Function: Use an optimization algorithm (usually stochastic gradient descent) to minimize the objective function. During this optimization, the word vectors are updated to better capture the co-occurrence patterns.
목적 함수 최적화: 최적화 알고리즘 (일반적으로 확률적 경사 하강법)을 사용하여 목적 함수를 최소화합니다. 이 최적화 과정에서 단어 벡터는 공기 발생 패턴을 더 잘 포착하기 위해 업데이트됩니다. - Extract Word Embeddings: Once training is complete, the learned word vectors serve as the word embeddings that capture semantic information about words.
단어 임베딩 추출: 훈련이 완료되면 학습된 단어 벡터는 의미 정보를 포착하는 단어 임베딩으로 사용됩니다.
GloVe embeddings have gained popularity due to their ability to capture meaningful semantic relationships between words, even without requiring extensive training data. They excel in capturing both syntactic (grammatical) and semantic (meaning-based) relationships, making them useful for a wide range of NLP tasks, such as text classification, sentiment analysis, machine translation, and more.
GloVe 임베딩은 광범위한 의미 관계를 캡처하는 능력으로 인해 풍부한 의미 정보를 기대할 수 없는 환경에서도 의미 있는 의미 관계를 포착하여 인기를 얻었습니다. 구문적 (문법적) 및 의미적 (의미 기반) 관계를 모두 잘 포착하여 텍스트 분류, 감성 분석, 기계 번역 등 다양한 NLP 작업에 유용합니다.
The GloVe model is an important advancement in the field of word embeddings and has contributed significantly to improving the quality of word representations used in various NLP applications.
GloVe 모델은 단어 임베딩 분야에서 중요한 진전으로, 다양한 NLP 응용 프로그램에서 사용되는 단어 표현의 품질을 크게 향상시키는 데 기여한 중요한 역할을 하고 있습니다.
15.5.4. Summary
- The skip-gram model can be interpreted using global corpus statistics such as word-word co-occurrence counts.
스킵그램 모델은 단어-단어 동시 발생 횟수와 같은 전역 코퍼스 통계를 사용하여 해석할 수 있습니다. - The cross-entropy loss may not be a good choice for measuring the difference of two probability distributions, especially for a large corpus. GloVe uses squared loss to fit precomputed global corpus statistics.
교차 엔트로피 손실은 특히 대규모 자료의 경우 두 확률 분포의 차이를 측정하는 데 좋은 선택이 아닐 수 있습니다. GloVe는 미리 계산된 글로벌 코퍼스 통계를 맞추기 위해 제곱 손실을 사용합니다. - The center word vector and the context word vector are mathematically equivalent for any word in GloVe.
중심 단어 벡터와 문맥 단어 벡터는 GloVe의 모든 단어에 대해 수학적으로 동일합니다. - GloVe can be interpreted from the ratio of word-word co-occurrence probabilities.
GloVe는 단어-단어 동시 출현 확률의 비율로 해석할 수 있습니다.
15.5.5. Exercises¶
- If words wi and wj co-occur in the same context window, how can we use their distance in the text sequence to redesign the method for calculating the conditional probability pij? Hint: see Section 4.2 of the GloVe paper (Pennington et al., 2014).
- For any word, are its center word bias and context word bias mathematically equivalent in GloVe? Why?
'Dive into Deep Learning > D2L Natural language Processing' 카테고리의 다른 글
| D2L - 15.10. Pretraining BERT (0) | 2023.08.30 |
|---|---|
| D2L - 15.9. The Dataset for Pretraining BERT (0) | 2023.08.30 |
| D2L - 15.8. Bidirectional Encoder Representations from Transformers (BERT) (0) | 2023.08.30 |
| D2L - 15.7. Word Similarity and Analogy (0) | 2023.08.30 |
| D2L - 15.6. Subword Embedding (0) | 2023.08.30 |
| D2L - 15.4. Pretraining word2vec (0) | 2023.08.29 |
| D2L - 15.3. The Dataset for Pretraining Word Embeddings (0) | 2023.08.29 |
| D2L- 15.2. Approximate Training (0) | 2023.08.28 |
| D2L- 15.1. Word Embedding (word2vec) (0) | 2023.08.25 |
| D2L - 15. Natural Language Processing: Pretraining (0) | 2023.08.24 |

