7.4. Multiple Input and Multiple Output Channels — Dive into Deep Learning 1.0.0-beta0 documentation
d2l.ai
7.4. Multiple Input and Multiple Output Channels
While we described the multiple channels that comprise each image (e.g., color images have the standard RGB channels to indicate the amount of red, green and blue) and convolutional layers for multiple channels in Section 7.1.4, until now, we simplified all of our numerical examples by working with just a single input and a single output channel. This allowed us to think of our inputs, convolution kernels, and outputs each as two-dimensional tensors.
섹션 7.1.4에서 각 이미지를 구성하는 여러 채널(예: 컬러 이미지에는 빨강, 녹색 및 파랑의 양을 나타내는 표준 RGB 채널이 있음)과 여러 채널에 대한 컨볼루션 레이어에 대해 설명했지만 지금까지 모든 이미지를 단순화했습니다. 단일 입력 및 단일 출력 채널로 작업하여 수치 예를 들어 보겠습니다. 이를 통해 입력, 컨볼루션 커널 및 출력을 각각 2차원 텐서로 생각할 수 있습니다.
When we add channels into the mix, our inputs and hidden representations both become three-dimensional tensors. For example, each RGB input image has shape 3×ℎ×w. We refer to this axis, with a size of 3, as the channel dimension. The notion of channels is as old as CNNs themselves. For instance LeNet5 (LeCun et al., 1995) uses them. In this section, we will take a deeper look at convolution kernels with multiple input and multiple output channels.
mix에 채널을 추가하면 입력과 hidden representations이 3차원 텐서가 됩니다. 예를 들어 각 RGB 입력 이미지의 모양은 3×ℎ×w입니다. 크기가 3인 이 축을 channel dimension이라고 합니다. 채널의 개념은 CNN 자체만큼이나 오래되었습니다. 예를 들어 LeNet5(LeCun et al., 1995)가 그것을 사용합니다. 이 섹션에서는 다중 입력 및 다중 출력 채널이 있는 컨볼루션 커널에 대해 자세히 살펴보겠습니다.
import torch
from d2l import torch as d2l
7.4.1. Multiple Input Channels
When the input data contains multiple channels, we need to construct a convolution kernel with the same number of input channels as the input data, so that it can perform cross-correlation with the input data. Assuming that the number of channels for the input data is ci, the number of input channels of the convolution kernel also needs to be ci. If our convolution kernel’s window shape is kℎ×kw, then when ci=1, we can think of our convolution kernel as just a two-dimensional tensor of shape kℎ×kw.
입력 데이터가 여러 채널을 포함하는 경우 입력 데이터와 상호 상관을 수행할 수 있도록 입력 데이터와 동일한 수의 입력 채널로 컨볼루션 커널을 구성해야 합니다. 입력 데이터의 채널 수가 ci라고 가정하면 컨볼루션 커널의 입력 채널 수도 ci가 되어야 합니다. 컨볼루션 커널의 창 모양이 kℎ×kw이면 ci=1일 때 컨볼루션 커널을 kℎ×kw 모양의 2차원 텐서로 생각할 수 있습니다.
However, when ci>1, we need a kernel that contains a tensor of shape kℎ×kw for every input channel. Concatenating these ci tensors together yields a convolution kernel of shape ci×kℎ×kw. Since the input and convolution kernel each have ci channels, we can perform a cross-correlation operation on the two-dimensional tensor of the input and the two-dimensional tensor of the convolution kernel for each channel, adding the ci results together (summing over the channels) to yield a two-dimensional tensor. This is the result of a two-dimensional cross-correlation between a multi-channel input and a multi-input-channel convolution kernel.
그러나 ci>1이면 모든 입력 채널에 대해 shape kℎ×kw의 텐서를 포함하는 커널이 필요합니다. 이 ci 텐서를 함께 연결하면 ci×kℎ×kw 모양의 컨볼루션 커널이 생성됩니다. 입력 및 컨볼루션 커널에는 각각 ci 채널이 있으므로 각 채널에 대한 입력의 2차원 텐서와 컨볼루션 커널의 2차원 텐서에 대해 cross-correlation 연산을 수행하여 ci 결과를 함께 더할 수 있습니다(합산 채널)을 사용하여 2차원 텐서를 생성합니다. 이것은 다중 채널 입력과 다중 입력 채널 컨볼루션 커널 사이의 2차원 cross-correlation의 결과입니다.
Fig. 7.4.1 provides an example of a two-dimensional cross-correlation with two input channels. The shaded portions are the first output element as well as the input and kernel tensor elements used for the output computation: (1×1+2×2+4×3+5×4)+(0×0+1×1+3×2+4×3)=56.
그림 7.4.1은 2개의 입력 채널이 있는 2차원 상호 상관의 예를 제공합니다. 음영 부분은 출력 계산에 사용되는 입력 및 커널 텐서 요소뿐만 아니라 첫 번째 출력 요소입니다. (1×1+2×2+4×3+5×4)+(0×0+1×1+ 3×2+4×3)=56.

To make sure we really understand what is going on here, we can implement cross-correlation operations with multiple input channels ourselves. Notice that all we are doing is performing a cross-correlation operation per channel and then adding up the results.
여기서 무슨 일이 일어나고 있는지 확실히 이해하기 위해 여러 입력 채널을 사용하여 상호 상관 작업을 직접 구현할 수 있습니다. 우리가 하는 일은 채널당 교차 상관 작업을 수행한 다음 결과를 합산하는 것뿐입니다.
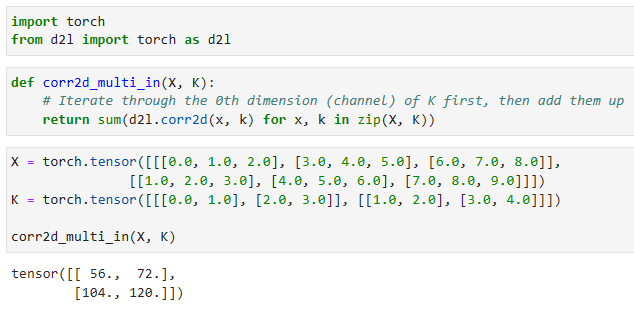
def corr2d_multi_in(X, K):
# Iterate through the 0th dimension (channel) of K first, then add them up
return sum(d2l.corr2d(x, k) for x, k in zip(X, K))- corr2d_multi_in 함수는 다중 입력 채널에 대한 2D 크로스-코릴레이션을 수행합니다.
- X는 입력 데이터를 나타내며, K는 커널을 나타냅니다.
- zip(X, K)를 사용하여 X와 K를 쌍으로 묶어 순회하면서 corr2d 함수를 적용한 결과를 모두 더하여 반환합니다.
https://www.programiz.com/python-programming/methods/built-in/zip
Python zip()
Python zip() In this tutorial, we will learn about the Python zip() function with the help of examples. The zip() function takes iterables (can be zero or more), aggregates them in a tuple, and returns it. Example languages = ['Java', 'Python', 'JavaScript
www.programiz.com
We can construct the input tensor X and the kernel tensor K corresponding to the values in Fig. 7.4.1 to validate the output of the cross-correlation operation.
그림 7.4.1의 값에 해당하는 입력 텐서 X와 커널 텐서 K를 구성하여 상호 상관 연산의 출력을 검증할 수 있습니다.
X = torch.tensor([[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
[[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]])
K = torch.tensor([[[0.0, 1.0], [2.0, 3.0]], [[1.0, 2.0], [3.0, 4.0]]])
corr2d_multi_in(X, K)- X는 입력 데이터를 나타내며, shape은 (2, 3, 3)입니다. 즉, 2개의 채널을 가지며 각 채널은 3x3 크기의 2D 행렬입니다.
- K는 커널을 나타내며, shape은 (2, 2, 2)입니다. 즉, 2개의 채널을 가지며 각 채널은 2x2 크기의 2D 행렬입니다.
- corr2d_multi_in(X, K)를 호출하여 X와 K의 다중 입력 채널에 대한 2D 크로스-코릴레이션을 계산합니다. 결과는 (2, 2) shape을 가진 2D 텐서로 반환됩니다.
7.4.2. Multiple Output Channels
Regardless of the number of input channels, so far we always ended up with one output channel. However, as we discussed in Section 7.1.4, it turns out to be essential to have multiple channels at each layer. In the most popular neural network architectures, we actually increase the channel dimension as we go deeper in the neural network, typically downsampling to trade off spatial resolution for greater channel depth. Intuitively, you could think of each channel as responding to a different set of features. The reality is a bit more complicated than this. A naive interpretation would suggest that representations are learned independently per pixel or per channel. Instead, channels are optimized to be jointly useful. This means that rather than mapping a single channel to an edge detector, it may simply mean that some direction in channel space corresponds to detecting edges.
입력 채널 수에 관계없이 지금까지 우리는 항상 하나의 출력 채널로 끝났습니다. 그러나 섹션 7.1.4에서 논의한 것처럼 각 계층에 여러 채널을 갖는 것이 필수적임이 밝혀졌습니다. 가장 널리 사용되는 신경망 아키텍처에서 우리는 신경망이 더 깊어짐에 따라 실제로 채널 차원을 증가시키고 일반적으로 더 큰 채널 깊이를 위해 공간 해상도를 절충하기 위해 다운샘플링합니다. 직관적으로 각 채널이 서로 다른 기능 집합에 응답한다고 생각할 수 있습니다. 현실은 이것보다 조금 더 복잡합니다. 순진한 해석은 표현이 픽셀 또는 채널별로 독립적으로 학습된다고 제안합니다. 대신 채널은 공동으로 유용하도록 최적화됩니다. 이는 단일 채널을 에지 검출기에 매핑하는 것이 아니라 단순히 채널 공간의 일부 방향이 에지 검출에 해당함을 의미할 수 있음을 의미합니다.
Denote by ci and co the number of input and output channels, respectively, and let kℎ and kw be the height and width of the kernel. To get an output with multiple channels, we can create a kernel tensor of shape ci×kℎ×kw for every output channel. We concatenate them on the output channel dimension, so that the shape of the convolution kernel is co×ci×kℎ×kw. In cross-correlation operations, the result on each output channel is calculated from the convolution kernel corresponding to that output channel and takes input from all channels in the input tensor.
ci 및 co는 각각 입력 및 출력 채널의 수를 나타내고 kℎ 및 kw는 커널의 높이 및 너비입니다. 여러 채널의 출력을 얻기 위해 모든 출력 채널에 대해 모양 ci×kℎ×kw의 커널 텐서를 만들 수 있습니다. 컨볼루션 커널의 모양이 co×ci×kℎ×kw가 되도록 출력 채널 차원에서 이들을 연결합니다. 교차 상관 연산에서 각 출력 채널의 결과는 해당 출력 채널에 해당하는 컨벌루션 커널에서 계산되며 입력 텐서의 모든 채널에서 입력을 받습니다.
We implement a cross-correlation function to calculate the output of multiple channels as shown below.
아래와 같이 여러 채널의 출력을 계산하기 위해 교차 상관 함수를 구현합니다.
def corr2d_multi_in_out(X, K):
# Iterate through the 0th dimension of K, and each time, perform
# cross-correlation operations with input X. All of the results are
# stacked together
return torch.stack([corr2d_multi_in(X, k) for k in K], 0)- X는 입력 데이터를 나타내며, shape은 (2, 3, 3)입니다. 즉, 2개의 입력 채널을 가지며 각 채널은 3x3 크기의 2D 행렬입니다.
- K는 커널을 나타내며, shape은 (3, 2, 2, 2)입니다. 즉, 3개의 입력 채널과 2개의 출력 채널을 가지며 각 채널은 2x2 크기의 2D 행렬입니다.
- corr2d_multi_in_out(X, K)를 호출하여 다중 입력 채널과 다중 출력 채널에 대한 2D 크로스-코릴레이션을 계산합니다. 결과는 (3, 2, 2) shape을 가진 3D 텐서로 반환됩니다.
We construct a trivial convolution kernel with 3 output channels by concatenating the kernel tensor for K with K+1 and K+2.
우리는 K에 대한 커널 텐서를 K+1 및 K+2와 연결하여 3개의 출력 채널이 있는 trivial convolution 커널을 구성합니다.
K = torch.stack((K, K + 1, K + 2), 0)
K.shape- K는 커널을 나타내는 텐서입니다.
- torch.stack((K, K + 1, K + 2), 0)를 사용하여 K의 차원 0을 따라 여러 개의 커널을 쌓습니다.
- 결과적으로 K의 shape은 (3, 2, 2, 2)가 됩니다. 즉, 3개의 커널을 가지며 각 커널은 2개의 입력 채널과 2개의 출력 채널을 가지는 2x2 크기의 2D 행렬입니다.

Below, we perform cross-correlation operations on the input tensor X with the kernel tensor K. Now the output contains 3 channels. The result of the first channel is consistent with the result of the previous input tensor X and the multi-input channel, single-output channel kernel.
아래에서는 입력 텐서 X와 커널 텐서 K에 대한 상호 상관 연산을 수행합니다. 이제 출력에는 3개의 채널이 포함됩니다. 첫 번째 채널의 결과는 이전 입력 텐서 X 및 다중 입력 채널, 단일 출력 채널 커널의 결과와 일치합니다.
corr2d_multi_in_out(X, K)- X는 입력 데이터를 나타내는 텐서입니다.
- K는 커널을 나타내는 텐서입니다.
- corr2d_multi_in_out(X, K) 함수는 K의 차원 0을 따라 반복하면서 X와의 크로스-코릴레이션 연산을 수행합니다.
- 결과적으로 모든 결과가 스택되어 텐서로 반환됩니다. 반환된 텐서의 shape은 (3, 1, 2, 2)가 됩니다. 즉, 3개의 커널을 가지며 각 커널은 1개의 입력 채널과 2개의 출력 채널을 가지는 2x2 크기의 2D 행렬입니다.

7.4.3. 1×1 Convolutional Layer
At first, a 1×1 convolution, i.e., kℎ=kw=1, does not seem to make much sense. After all, a convolution correlates adjacent pixels. A 1×1 convolution obviously does not. Nonetheless, they are popular operations that are sometimes included in the designs of complex deep networks (Lin et al., 2013, Szegedy et al., 2017) Let’s see in some detail what it actually does.
처음에는 1×1 컨벌루션, 즉 kℎ=kw=1이 별 의미가 없는 것 같습니다. 결국 컨볼루션은 인접한 픽셀을 연관시킵니다. 1×1 컨볼루션은 분명히 그렇지 않습니다. 그럼에도 불구하고 복잡한 심층 네트워크의 설계에 때때로 포함되는 인기 있는 작업입니다(Lin et al., 2013, Szegedy et al., 2017) 실제로 어떤 일을 하는지 자세히 살펴보겠습니다.
Because the minimum window is used, the 1×1 convolution loses the ability of larger convolutional layers to recognize patterns consisting of interactions among adjacent elements in the height and width dimensions. The only computation of the 1×1 convolution occurs on the channel dimension.
minimum window이 사용되기 때문에 1×1 컨볼루션은 높이와 너비 차원에서 인접한 요소 간의 상호 작용으로 구성된 패턴을 인식하는 더 큰 컨볼루션 레이어의 기능을 잃습니다. 1×1 컨벌루션의 유일한 계산은 채널 차원에서 발생합니다.
Fig. 7.4.2 shows the cross-correlation computation using the 1×1 convolution kernel with 3 input channels and 2 output channels. Note that the inputs and outputs have the same height and width. Each element in the output is derived from a linear combination of elements at the same position in the input image. You could think of the 1×1 convolutional layer as constituting a fully connected layer applied at every single pixel location to transform the ci corresponding input values into c0 output values. Because this is still a convolutional layer, the weights are tied across pixel location. Thus the 1×1 convolutional layer requires co×ci weights (plus the bias). Also note that convolutional layers are typically followed by nonlinearities. This ensures that 1×1 convolutions cannot simply be folded into other convolutions.
그림 7.4.2는 3개의 입력 채널과 2개의 출력 채널이 있는 1×1 컨볼루션 커널을 사용한 교차 상관 계산을 보여줍니다. 입력과 출력의 높이와 너비는 동일합니다. 출력의 각 요소는 입력 이미지의 동일한 위치에 있는 요소의 선형 조합에서 파생됩니다. 1×1 컨벌루션 레이어는 모든 단일 픽셀 위치에 적용되는 완전 연결 레이어를 구성하여 ci 해당 입력 값을 c0 출력 값으로 변환하는 것으로 생각할 수 있습니다. 이것은 여전히 컨볼루션 레이어이기 때문에 가중치는 픽셀 위치 전체에 묶여 있습니다. 따라서 1×1 컨벌루션 레이어에는 co×ci 가중치(바이어스 포함)가 필요합니다. 또한 컨볼루션 레이어 다음에는 일반적으로 비선형성이 뒤따릅니다. 이렇게 하면 1×1 컨볼루션이 단순히 다른 컨볼루션으로 접힐 수 없습니다.

Let’s check whether this works in practice: we implement a 1×1 convolution using a fully connected layer. The only thing is that we need to make some adjustments to the data shape before and after the matrix multiplication.
이것이 실제로 작동하는지 확인해 보겠습니다. 완전 연결 레이어를 사용하여 1×1 컨볼루션을 구현합니다. 유일한 것은 행렬 곱셈 전후에 데이터 모양을 약간 조정해야 한다는 것입니다.
def corr2d_multi_in_out_1x1(X, K):
c_i, h, w = X.shape
c_o = K.shape[0]
X = X.reshape((c_i, h * w))
K = K.reshape((c_o, c_i))
# Matrix multiplication in the fully connected layer
Y = torch.matmul(K, X)
return Y.reshape((c_o, h, w))- X는 입력 데이터를 나타내는 텐서입니다.
- K는 커널을 나타내는 텐서입니다.
- c_i, h, w는 X의 차원을 나타냅니다. c_i는 입력 채널의 개수, h는 높이, w는 너비입니다.
- c_o는 K의 차원 0의 크기로, 출력 채널의 개수를 나타냅니다.
- X와 K를 형태에 맞게 재조정합니다. X는 (c_i, h * w) 형태로, K는 (c_o, c_i) 형태로 재조정됩니다.
- 행렬 곱셈을 통해 완전 연결 층에서의 계산을 수행합니다. Y = torch.matmul(K, X)를 통해 결과를 얻습니다.
- 최종적으로 Y를 (c_o, h, w) 형태로 재조정하여 반환합니다. 즉, 출력 채널 개수가 c_o이고 높이와 너비가 같은 2D 텐서를 반환합니다.
When performing 1×1 convolutions, the above function is equivalent to the previously implemented cross-correlation function corr2d_multi_in_out. Let’s check this with some sample data.
1×1 컨벌루션을 수행할 때 위의 함수는 이전에 구현된 교차 상관 함수 corr2d_multi_in_out과 동일합니다. 몇 가지 샘플 데이터로 이를 확인해보자.
X = torch.normal(0, 1, (3, 3, 3))
K = torch.normal(0, 1, (2, 3, 1, 1))
Y1 = corr2d_multi_in_out_1x1(X, K)
Y2 = corr2d_multi_in_out(X, K)
assert float(torch.abs(Y1 - Y2).sum()) < 1e-6- X는 평균 0, 표준 편차 1인 정규 분포를 따르는 3차원 텐서입니다. 크기는 (3, 3, 3)입니다.
- K는 평균 0, 표준 편차 1인 정규 분포를 따르는 4차원 텐서입니다. 크기는 (2, 3, 1, 1)입니다. 이는 1x1 커널을 사용하는 다중 입력 다중 출력(conv2d_multi_in_out_1x1) 연산에 사용됩니다.
- Y1은 X와 K를 사용하여 1x1 커널을 적용한 다중 입력 다중 출력(conv2d_multi_in_out_1x1) 연산의 결과입니다.
- Y2는 X와 K를 사용하여 일반적인 다중 입력 다중 출력(conv2d_multi_in_out) 연산의 결과입니다.
- Y1과 Y2의 차이를 절댓값으로 계산하고 그 합이 1e-6보다 작은지 확인합니다. 즉, 두 연산의 결과가 거의 동일한지 확인하는 검증(assert)입니다.
7.4.4. Discussion
Channels allow us to combine the best of both worlds: MLPs that allow for significant nonlinearities and convolutions that allow for localized analysis of features. In particular, channels allow the CNN to reason with multiple features, such as edge and shape detectors at the same time. They also offer a practical trade-off between the drastic parameter reduction arising from translation invariance and locality, and the need for expressive and diverse models in computer vision.
채널을 통해 두 세계의 장점을 결합할 수 있습니다. 중요한 비선형성을 허용하는 MLP와 기능의 국지적 분석을 허용하는 컨볼루션입니다. 특히 채널을 통해 CNN은 모서리 및 모양 감지기와 같은 여러 기능을 동시에 추론할 수 있습니다. 또한 변환 불변성 및 지역성으로 인해 발생하는 급격한 매개변수 감소와 컴퓨터 비전에서 표현적이고 다양한 모델에 대한 필요성 사이의 실용적인 절충안을 제공합니다.

그러나 이러한 유연성에는 대가가 따른다는 점에 유의하십시오. 크기가 (ℎ×w)인 이미지가 주어지면 k×k 컨벌루션을 계산하는 비용은 O(ℎ⋅w⋅k2)입니다. ci 및 co 입력 및 출력 채널의 경우 각각 O(ℎ⋅w⋅k2⋅ci⋅co)로 증가합니다. 5×5 커널과 각각 128개의 입력 및 출력 채널이 있는 256×256 픽셀 이미지의 경우 이는 530억 개가 넘는 작업에 해당합니다(곱셈과 덧셈은 별도로 계산함). 나중에 우리는 ResNeXt(Xie et al., 2017)와 같은 아키텍처로 이어지는 채널별 작업이 블록 대각선이 되도록 요구함으로써 비용을 절감하는 효과적인 전략에 직면하게 될 것입니다.
7.4.5. Exercises

'Dive into Deep Learning > D2L Convolutional Neural Networks (CNN)' 카테고리의 다른 글
| D2L - 8.3. Network in Network (NiN) (0) | 2023.07.11 |
|---|---|
| D2L - 8.2. Networks Using Blocks (VGG) (0) | 2023.07.10 |
| D2L - 8.1. Deep Convolutional Neural Networks (AlexNet) (0) | 2023.07.10 |
| D2L - 8. Modern Convolutional Neural Networks (0) | 2023.07.10 |
| D2L - 7.6. Convolutional Neural Networks (LeNet) (0) | 2023.07.09 |
| D2L - 7.5. Pooling (1) | 2023.07.09 |
| D2L - 7.3. Padding and Stride (0) | 2023.07.09 |
| D2L - 7.2. Convolutions for Images (0) | 2023.07.09 |
| D2L - 7.1. From Fully Connected Layers to Convolutions (0) | 2023.07.09 |
| D2L - 7. Convolutional Neural Networks (0) | 2023.07.09 |

