D2L - 7.5. Pooling
2023. 7. 9. 21:27 |
7.5. Pooling — Dive into Deep Learning 1.0.0-beta0 documentation (d2l.ai)
7.5. Pooling — Dive into Deep Learning 1.0.0-beta0 documentation
d2l.ai
7.5. Pooling
In many cases our ultimate task asks some global question about the image, e.g., does it contain a cat? Consequently, the units of our final layer should be sensitive to the entire input. By gradually aggregating information, yielding coarser and coarser maps, we accomplish this goal of ultimately learning a global representation, while keeping all of the advantages of convolutional layers at the intermediate layers of processing. The deeper we go in the network, the larger the receptive field (relative to the input) to which each hidden node is sensitive. Reducing spatial resolution accelerates this process, since the convolution kernels cover a larger effective area.
많은 경우에 우리의 궁극적인 작업은 이미지에 대한 전반적인 질문을 합니다. (예: 고양이가 포함되어 있습니까?) 결과적으로 최종 레이어의 단위는 전체 입력에 민감해야 합니다. 점진적으로 정보를 집계하고 더 거칠고(coarser) 더 거친(coarser) 맵을 생성함으로써 우리는 궁극적으로 글로벌 표현(global representation)을 학습하는 동시에 중간 처리 레이어에서 컨볼루션 레이어의 모든 이점을 유지한다는 목표를 달성합니다. 네트워크에 깊이 들어갈수록 각 hidden node는 민감해 지면서 수용(receptive ) 필드(입력에 비해)가 커집니다. 컨볼루션 커널이 더 큰 유효 영역을 다루기 때문에 공간 해상도(spatial resolution)를 줄이면 이 프로세스가 가속화됩니다.
Moreover, when detecting lower-level features, such as edges (as discussed in Section 7.2), we often want our representations to be somewhat invariant to translation. For instance, if we take the image X with a sharp delineation between black and white and shift the whole image by one pixel to the right, i.e., Z[i, j] = X[i, j + 1], then the output for the new image Z might be vastly different. The edge will have shifted by one pixel. In reality, objects hardly ever occur exactly at the same place. In fact, even with a tripod and a stationary object, vibration of the camera due to the movement of the shutter might shift everything by a pixel or so (high-end cameras are loaded with special features to address this problem).
더욱 이 에지와 같은 lower-level features을 detecting 할 때(섹션 7.2에서 논의됨) 우리는 종종 우리의 표현(representations )이 translation 면에서 다소 불변하기를 원합니다. 예를 들어, 검은색과 흰색 사이의 뚜렷한 경계가 있는 이미지 X를 취하고 전체 이미지를 오른쪽으로 한 픽셀씩 이동하면(즉, Z[i, j] = X[i, j + 1]) 그러면 새 이미지 Z에 대한 출력은 크게 다를 수 있습니다. 가장자리가 1픽셀씩 이동하게 될 겁니다. 실제로는 물체가 정확히 같은 장소에 있는 경우는 거의 없습니다. 사실 삼각대와 고정된 물체가 있더라도 셔터 누를때의 움직임 때문에 카메라가 약간이라도 흔들려서 모든 것들은 1픽셀이나 그 이상 움직일 수 있습니다. (고급 카메라에는 이 문제를 해결하기 위한 특수 기능이 탑재되어 있습니다).
This section introduces pooling layers, which serve the dual purposes of mitigating the sensitivity of convolutional layers to location and of spatially downsampling representations.
이 섹션에서는 위치에 대한 컨볼루션 레이어의 민감도와 공간적 다운샘플링 표현의 민감도를 완화하는 이중 목적을 제공하는 풀링 레이어(pooling layers)를 소개합니다.
import torch
from torch import nn
from d2l import torch as d2l
7.5.1. Maximum Pooling and Average Pooling
Like convolutional layers, pooling operators consist of a fixed-shape window that is slid over all regions in the input according to its stride, computing a single output for each location traversed by the fixed-shape window (sometimes known as the pooling window). However, unlike the cross-correlation computation of the inputs and kernels in the convolutional layer, the pooling layer contains no parameters (there is no kernel). Instead, pooling operators are deterministic, typically calculating either the maximum or the average value of the elements in the pooling window. These operations are called maximum pooling (max-pooling for short) and average pooling, respectively.
컨벌루션 레이어와 마찬가지로 풀링 연산자는 보폭(stride)에 따라 입력의 모든 영역에서 미끄러지는 고정 모양 창(fixed-shape window)으로 구성되며 고정 모양 창(풀링 창이라고도 함)이 통과하는 각 위치에 대해 단일 출력을 계산합니다. 그러나 컨벌루션 계층의 입력 및 커널의 상호 상관(cross-correlation) 계산과 달리 풀링 계층에는 매개 변수가 없습니다 (커널이 없음). 대신 풀링 연산자는 결정적(deterministic)이며 일반적으로 풀링 창에 있는 요소의 최대값(maximum ) 또는 평균값(average )을 계산합니다. 이러한 작업을 각각 maximum pooling(줄여서 max-pooling) 및 평균 풀링(average pooling)이라고 합니다.
Average pooling is essentially as old as CNNs. The idea is akin to downsampling an image. Rather than just taking the value of every second (or third) pixel for the lower resolution image, we can average over adjacent pixels to obtain an image with better signal to noise ratio since we are combining the information from multiple adjacent pixels. Max-pooling was introduced in Riesenhuber and Poggio (1999) in the context of cognitive neuroscience to describe how information aggregation might be aggregated hierarchically for the purpose of object recognition, and an earlier version in speech recognition (Yamaguchi et al., 1990). In almost all cases, max-pooling, as it is also referred to, is preferable.
평균 풀링(Average pooling)은 기본적으로 CNN만큼 오래되었습니다. 아이디어는 이미지를 다운샘플링하는 것과 유사합니다. 저해상도 이미지에 대해 모든 두 번째(또는 세 번째) 픽셀의 값을 취하는 대신 여러 인접 픽셀의 정보를 결합하므로 인접 픽셀에 대해 평균을 내어 더 나은 신호 대 노이즈 비율을 가진 이미지를 얻을 수 있습니다. Max-pooling은 Riesenhuber와 Poggio(1999)에서 객체 인식을 위해 정보 집계가 계층적으로 집계되는 방법을 설명하기 위해 인지 신경과학의 맥락에서 도입되었으며 음성 인식의 초기 버전(Yamaguchi et al., 1990)입니다. 거의 모든 경우에 최대 풀링(max-pooling)이 선호됩니다.
In both cases, as with the cross-correlation operator, we can think of the pooling window as starting from the upper-left of the input tensor and sliding across the input tensor from left to right and top to bottom. At each location that the pooling window hits, it computes the maximum or average value of the input subtensor in the window, depending on whether max or average pooling is employed.
두 경우 모두 cross-correlation 연산자와 마찬가지로 풀링 창을 입력 텐서의 왼쪽 상단에서 시작하여 입력 텐서를 가로질러 왼쪽에서 오른쪽으로 그리고 위에서 아래로 미끄러지는 것으로 생각할 수 있습니다. 풀링 윈도우가 도달하는 각 위치에서 최대 또는 평균 풀링이 사용되는지 여부에 따라 윈도우에서 입력 하위 텐서의 최대값 또는 평균값을 계산합니다.
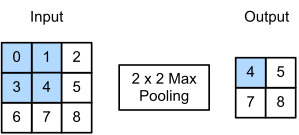
The output tensor in Fig. 7.5.1 has a height of 2 and a width of 2. The four elements are derived from the maximum value in each pooling window:
그림 7.5.1의 출력 텐서는 높이가 2이고 너비가 2입니다. 4개의 요소는 각 풀링 창의 최대값에서 파생됩니다.

More generally, we can define a p×q pooling layer by aggregating over a region of said size. Returning to the problem of edge detection, we use the output of the convolutional layer as input for 2×2 max-pooling. Denote by X the input of the convolutional layer input and Y the pooling layer output. Regardless of whether or not the values of X[i, j], X[i, j + 1], X[i+1, j] and X[i+1, j + 1] are different, the pooling layer always outputs Y[i, j] = 1. That is to say, using the 2×2 max-pooling layer, we can still detect if the pattern recognized by the convolutional layer moves no more than one element in height or width.
보다 일반적으로, 우리는 상기 크기의 영역을 집계하여 p×q 풀링 계층을 정의할 수 있습니다. 에지 감지 문제로 돌아가서 컨볼루션 레이어의 출력을 2×2 최대 풀링의 입력으로 사용합니다. X는 컨벌루션 계층 입력의 입력을 나타내고 Y는 풀링 계층 출력을 나타냅니다. X[i, j], X[i, j + 1], X[i+1, j] 및 X[i+1, j + 1]의 값이 다른지 여부에 관계없이 pooling layer는 항상 Y[i, j] = 1을 출력합니다. 즉, 2×2 최대 풀링 레이어를 사용하여 컨볼루션 레이어에서 인식한 패턴이 높이 또는 너비에서 하나의 요소만 이동하는지 여전히 감지할 수 있습니다.
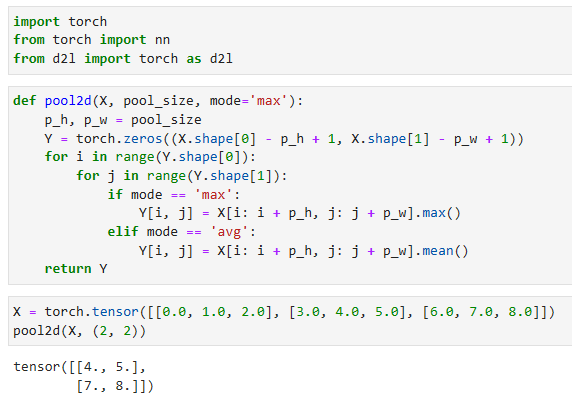
In the code below, we implement the forward propagation of the pooling layer in the pool2d function. This function is similar to the corr2d function in Section 7.2. However, no kernel is needed, computing the output as either the maximum or the average of each region in the input.
아래 코드에서는 pool2d 함수에서 풀링 계층의 순방향 전파를 구현합니다. 이 함수는 섹션 7.2의 corr2d 함수와 유사합니다. 그러나 커널이 필요하지 않으며 입력에서 각 영역의 최대 또는 평균으로 출력을 계산합니다.
def pool2d(X, pool_size, mode='max'):
p_h, p_w = pool_size
Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
if mode == 'max':
Y[i, j] = X[i: i + p_h, j: j + p_w].max()
elif mode == 'avg':
Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
return Y- X는 입력 데이터로, 2차원 텐서입니다.
- pool_size는 풀링 윈도우의 크기를 지정하는 튜플 (p_h, p_w)입니다.
- mode는 풀링 모드를 선택하는 매개변수로, 'max' 또는 'avg'로 설정할 수 있습니다.
- Y는 풀링 연산의 결과로, 입력 X의 차원을 줄여 나온 2차원 텐서입니다.
- for 반복문을 사용하여 X의 각 위치에 대해 풀링 연산을 수행합니다.
- mode가 'max'인 경우, 해당 위치의 풀링 윈도우에서 가장 큰 값을 선택하여 Y에 저장합니다.
- mode가 'avg'인 경우, 해당 위치의 풀링 윈도우의 평균 값을 계산하여 Y에 저장합니다.
- 최종적으로 Y를 반환합니다.
We can construct the input tensor X in Fig. 7.5.1 to validate the output of the two-dimensional max-pooling layer.
그림 7.5.1에서 입력 텐서 X를 구성하여 2차원 최대 풀링 레이어의 출력을 검증할 수 있습니다.
X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
pool2d(X, (2, 2))- X는 입력 데이터로, 2차원 텐서입니다.
- (2, 2)는 풀링 윈도우의 크기를 나타내는 튜플입니다.
- pool2d 함수를 호출하여 입력 X에 대해 2x2 크기의 풀링 연산을 수행합니다.
- 풀링 연산은 주어진 윈도우 크기 내에서 최대값 또는 평균값을 계산하여 결과 텐서를 반환합니다.
- 반환된 결과 텐서는 입력 X의 크기를 줄여 2차원 텐서로 나타냅니다.
Also, we experiment with the average pooling layer.
또한 평균 풀링 계층을 실험합니다.
pool2d(X, (2, 2), 'avg')
7.5.2. Padding and Stride
As with convolutional layers, pooling layers change the output shape. And as before, we can adjust the operation to achieve a desired output shape by padding the input and adjusting the stride. We can demonstrate the use of padding and strides in pooling layers via the built-in two-dimensional max-pooling layer from the deep learning framework. We first construct an input tensor X whose shape has four dimensions, where the number of examples (batch size) and number of channels are both 1.
컨벌루션 레이어와 마찬가지로 풀링 레이어는 출력 형태(output shape)를 변경합니다. 이전과 마찬가지로 입력을 패딩하고 보폭(stride)을 조정하여 원하는 출력 모양을 얻기 위해 작업을 조정할 수 있습니다. 딥 러닝 프레임워크의 built-in two-dimensional max-pooling layer 을 통해 풀링 계층에서 패딩 및 strides 의 사용을 시연할 수 있습니다. 먼저 모양이 4차원인 입력 텐서 X를 구성합니다. 여기서 예제 수(배치 크기)와 채널 수는 모두 1입니다.
X = torch.arange(16, dtype=torch.float32).reshape((1, 1, 4, 4))
X- torch.arange(16, dtype=torch.float32)는 0부터 15까지의 값을 가지는 1차원 텐서를 생성합니다.
- .reshape((1, 1, 4, 4))는 생성된 1차원 텐서를 4x4 크기의 2차원 텐서로 변형합니다.
- X는 변형된 2차원 텐서로, 형태는 (1, 1, 4, 4)입니다.
- 이는 배치 크기가 1이고 채널 수가 1인 4x4 크기의 이미지를 의미합니다.

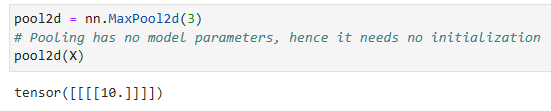
Since pooling aggregates information from an area, deep learning frameworks default to matching pooling window sizes and stride. For instance, if we use a pooling window of shape (3, 3) we get a stride shape of (3, 3) by default.
풀링은 한 area에서 정보를 집계하므로 딥 러닝 프레임워크는 기본적으로 일치하는 풀링 창 크기 및 보폭(stride)을 사용합니다. 예를 들어 모양이 (3, 3)인 풀링 창을 사용하면 기본적으로 stride 모양이 (3, 3)이 됩니다.
pool2d = nn.MaxPool2d(3)
# Pooling has no model parameters, hence it needs no initialization
pool2d(X)- nn.MaxPool2d(3)는 3x3 크기의 Max Pooling 연산을 수행하는 풀링 레이어를 생성합니다.
- 풀링 레이어는 모델 파라미터가 없으므로 초기화할 필요가 없습니다.
- pool2d(X)는 입력 X에 대해 Max Pooling 연산을 수행한 결과를 반환합니다.
- 이는 입력 이미지에서 3x3 윈도우로 최대값을 추출하여 다운샘플링한 결과입니다.
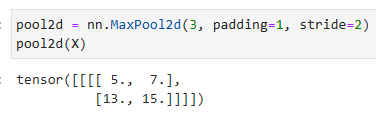
As expected, the stride and padding can be manually specified to override framework defaults if needed.
예상대로 stride 과 패딩을 수동으로 특정하여 필요한 경우 프레임워크 기본값을 재정의할 수 있습니다.
pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)- nn.MaxPool2d(3, padding=1, stride=2)는 3x3 크기의 Max Pooling 연산을 수행하는 풀링 레이어를 생성합니다.
- padding=1은 입력에 대해 패딩을 적용하여 출력 크기를 유지합니다. 패딩 값은 1입니다.
- stride=2는 풀링 연산을 수행할 때 2칸씩 이동하면서 다운샘플링합니다.
- pool2d(X)는 입력 X에 대해 Max Pooling 연산을 수행한 결과를 반환합니다.
- 이는 입력 이미지에서 3x3 윈도우로 최대값을 추출하고, 패딩을 적용하여 출력 크기를 유지하며, 2칸씩 이동하면서 다운샘플링한 결과입니다.
Of course, we can specify an arbitrary rectangular pooling window with arbitrary height and width respectively, as the example below shows.
물론 아래 예제와 같이 임의의 높이와 너비를 가진 임의의 직사각형 풀링 창(arbitrary rectangular pooling window)을 지정할 수 있습니다.
pool2d = nn.MaxPool2d((2, 3), stride=(2, 3), padding=(0, 1))
pool2d(X)- nn.MaxPool2d((2, 3), stride=(2, 3), padding=(0, 1))는 2x3 크기의 Max Pooling 연산을 수행하는 풀링 레이어를 생성합니다.
- (2, 3)은 풀링 윈도우의 크기를 지정합니다. 여기서는 2x3 크기의 윈도우를 사용합니다.
- stride=(2, 3)는 풀링 연산을 수행할 때 2칸씩 수평 방향으로 이동하고 3칸씩 수직 방향으로 이동하면서 다운샘플링합니다.
- padding=(0, 1)은 입력에 대해 패딩을 적용하여 출력 크기를 유지합니다. 수직 방향으로만 패딩을 적용하며, 위쪽에는 패딩이 없고 아래쪽에는 1칸의 패딩을 적용합니다.
- pool2d(X)는 입력 X에 대해 Max Pooling 연산을 수행한 결과를 반환합니다.
- 이는 입력 이미지에서 2x3 크기의 윈도우로 최대값을 추출하고, 수평과 수직 방향으로 지정된 stride만큼 이동하면서 다운샘플링한 결과입니다. 패딩을 적용하여 출력 크기를 유지합니다.

7.5.3. Multiple Channels
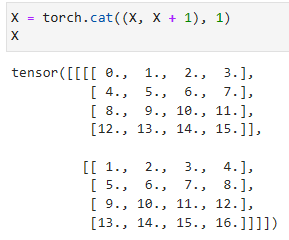
When processing multi-channel input data, the pooling layer pools each input channel separately, rather than summing the inputs up over channels as in a convolutional layer. This means that the number of output channels for the pooling layer is the same as the number of input channels. Below, we will concatenate tensors X and X + 1 on the channel dimension to construct an input with 2 channels.
다중 채널 입력 데이터를 처리할 때 풀링 계층은 컨벌루션 계층에서와 같이 채널을 통해 입력을 합산하는 대신 각 입력 채널을 개별적으로 풀링합니다. 이는 풀링 레이어의 출력 채널 수가 입력 채널 수와 같다는 것을 의미합니다. 아래에서는 채널 차원에서 텐서 X와 X + 1을 연결하여 2개의 채널이 있는 입력을 구성합니다.
X = torch.cat((X, X + 1), 1)
X- torch.cat((X, X + 1), 1)은 텐서 X와 X + 1을 수평 방향(axis 1)으로 연결하는 연산입니다.
- X와 X + 1은 같은 크기의 텐서이며, 수평 방향으로 연결하면 총 2개의 텐서가 결합된 결과를 반환합니다.
- 따라서 X는 첫 번째 차원(axis 0)을 유지하고 수평 방향으로 결합된 텐서입니다.
- X는 결합된 결과를 나타내며, 연결된 두 개의 텐서가 수평으로 이어져 있습니다.
https://pytorch.org/docs/stable/generated/torch.cat.html
torch.cat — PyTorch 2.0 documentation
Shortcuts
pytorch.org
As we can see, the number of output channels is still 2 after pooling.
보시다시피 출력 채널 수는 풀링 후에도 여전히 2개입니다.
pool2d = nn.MaxPool2d(3, padding=1, stride=2)
pool2d(X)- nn.MaxPool2d(3, padding=1, stride=2)은 최대 풀링(max pooling)을 수행하는 2D 풀링 레이어입니다.
- 이 풀링 레이어는 입력 데이터를 3x3 윈도우로 슬라이딩하면서 각 윈도우 영역의 최댓값을 출력으로 반환합니다.
- padding=1은 입력 데이터 주변에 1픽셀만큼의 패딩을 추가하는 것을 의미합니다. 이를 통해 입력 데이터의 크기를 보존하면서 풀링 연산을 수행합니다.
- stride=2는 윈도우를 이동시키는 간격을 나타냅니다. 이 경우, 각 풀링 영역을 2픽셀씩 이동시킵니다.
- pool2d(X)는 입력 데이터 X에 대해 최대 풀링 연산을 수행한 결과를 반환합니다.
- 최대 풀링은 입력 데이터를 윈도우로 나누고 각 윈도우 영역에서 최댓값을 추출하는 연산입니다.
- 반환된 결과는 입력 데이터를 3x3 윈도우로 슬라이딩하면서 최댓값을 추출한 결과로 이루어진 텐서입니다.
- 출력 텐서의 크기는 입력 데이터의 크기에 영향을 받으며, 패딩과 스트라이드에 따라서도 달라질 수 있습니다.

https://pytorch.org/docs/stable/generated/torch.nn.MaxPool2d.html
MaxPool2d — PyTorch 2.0 documentation
Shortcuts
pytorch.org
7.5.4. Summary
Pooling is an exceedingly simple operation. It does exactly what its name indicates, aggregate results over a window of values. All convolution semantics, such as strides and padding apply in the same way as they did previously. Note that pooling is indifferent to channels, i.e., it leaves the number of channels unchanged and it applies to each channel separately. Lastly, of the two popular pooling choices, max-pooling is preferable to average pooling, as it confers some degree of invariance to output. A popular choice is to pick a pooling window size of 2×2 to quarter the spatial resolution of output.
풀링은 매우 간단한 작업입니다. 이름이 나타내는 것과 정확히 일치하며 값 창에서 결과를 집계합니다. 보폭(stride) 및 패딩과 같은 모든 컨볼루션 시맨틱은 이전과 동일한 방식으로 적용됩니다. 풀링은 채널과 무관합니다. 즉, 채널 수를 변경하지 않고 각 채널에 개별적으로 적용합니다. 마지막으로 인기 있는 두 가지 풀링 선택 중에서 최대 풀링이 평균 풀링보다 선호되는데, 이는 출력에 어느 정도의 불변성을 부여하기 때문입니다. 대중적인 선택은 2×2의 풀링 창 크기를 선택하여 출력의 공간 해상도를 4분의 1로 줄이는 것입니다.
Note that there are many more ways of reducing resolution beyond pooling. For instance, in stochastic pooling (Zeiler and Fergus, 2013) and fractional max-pooling (Graham, 2014) aggregation is combined with randomization. This can slightly improve the accuracy in some cases. Lastly, as we will see later with the attention mechanism, there are more refined ways of aggregating over outputs, e.g., by using the alignment between a query and representation vectors.
풀링 외에도 해상도를 줄이는 더 많은 방법이 있습니다. 예를 들어 확률적 풀링(Zeiler and Fergus, 2013) 및 분수 최대 풀링(Graham, 2014)에서 집계는 무작위화와 결합됩니다. 이것은 경우에 따라 정확도를 약간 향상시킬 수 있습니다. 마지막으로 주의 메커니즘에 대해 나중에 살펴보겠지만 쿼리와 표현 벡터 사이의 정렬을 사용하여 출력을 집계하는 보다 세련된 방법이 있습니다.
7.5.5. Exercises

'Dive into Deep Learning > D2L Convolutional Neural Networks (CNN)' 카테고리의 다른 글
| D2L - 8.3. Network in Network (NiN) (0) | 2023.07.11 |
|---|---|
| D2L - 8.2. Networks Using Blocks (VGG) (0) | 2023.07.10 |
| D2L - 8.1. Deep Convolutional Neural Networks (AlexNet) (0) | 2023.07.10 |
| D2L - 8. Modern Convolutional Neural Networks (0) | 2023.07.10 |
| D2L - 7.6. Convolutional Neural Networks (LeNet) (0) | 2023.07.09 |
| D2L - 7.4. Multiple Input and Multiple Output Channels (0) | 2023.07.09 |
| D2L - 7.3. Padding and Stride (0) | 2023.07.09 |
| D2L - 7.2. Convolutions for Images (0) | 2023.07.09 |
| D2L - 7.1. From Fully Connected Layers to Convolutions (0) | 2023.07.09 |
| D2L - 7. Convolutional Neural Networks (0) | 2023.07.09 |

