https://d2l.ai/chapter_attention-mechanisms-and-transformers/attention-pooling.html
11.2. Attention Pooling by Similarity — Dive into Deep Learning 1.0.0-beta0 documentation
d2l.ai
11.2. Attention Pooling by Similarity
Now that we introduced the primary components of the attention mechanism, let’s use them in a rather classical setting, namely regression and classification via kernel density estimation (Nadaraya, 1964, Watson, 1964). This detour simply provides additional background: it is entirely optional and can be skipped if needed. At their core, Nadaraya-Watson estimators rely on some similarity kernel α(q,k) relating queries q to keys k. Some common kernels are
어텐션 메커니즘의 주요 구성 요소를 소개했으므로 이제 이를 다소 고전적인 설정, 즉 커널 밀도 추정(kernel density estimation)을 통한 회귀 및 분류(regression and classification)에서 사용하겠습니다(Nadaraya, 1964, Watson, 1964). 이 detour 는 단순히 추가 배경을 제공합니다. 완전히 선택 사항이며 필요한 경우 건너뛸 수 있습니다. 그들의 핵심에서 Nadaraya-Watson 추정기는 쿼리 q와 키 k를 관련시키는 몇 가지 유사성 커널 α(q,k)에 의존합니다. 일부 일반적인 커널은 다음과 같습니다.
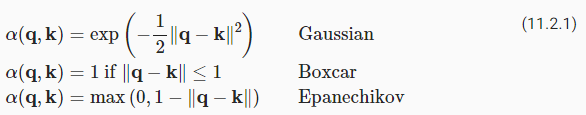
There are many more choices that we could pick. See a Wikipedia article for a more extensive review and how the choice of kernels is related to kernel density estimation, sometimes also called Parzen Windows (Parzen, 1957). All of the kernels are heuristic and can be tuned. For instance, we can adjust the width, not only on a global basis but even on a per-coordinate basis. Regardless, all of them lead to the following equation for regression and classification alike:
우리가 고를 수 있는 더 많은 선택이 있습니다. 보다 광범위한 review 및 커널 선택이 kernel density estimation(때때로 Parzen Windows라고도 함)과 어떻게 관련되는지에 대해서는 Wikipedia 기사를 참조하십시오(Parzen, 1957). 모든 커널은 경험적(heuristic)이며 조정할 수 있습니다. 예를 들어 전역 기준뿐만 아니라 좌표 단위로도 너비를 조정할 수 있습니다. 그럼에도 불구하고 모두 회귀(regression ) 및 분류(classification )에 대해 다음과 같은 방정식으로 이어집니다.

In the case of a (scalar) regression with observations (xi,yi) for features and labels respectively, vi=yi are scalars, ki=xi are vectors, and the query q denotes the new location where f should be evaluated. In the case of (multiclass) classification, we use one-hot-encoding of yi to obtain vi. One of the convenient properties of this estimator is that it requires no training. Even more so, if we suitably narrow the kernel with increasing amounts of data, the approach is consistent (Mack and Silverman, 1982), i.e., it will converge to some statistically optimal solution. Let’s start by inspecting some kernels.
features 와 labels 에 대한 관찰값(xi,yi)이 있는 (스칼라) 회귀의 경우 vi=yi는 스칼라이고 ki=xi는 벡터이며 쿼리 q는 f를 평가해야 하는 새 위치를 나타냅니다. (다중 클래스) classification의 경우 vi를 얻기 위해 yi의 one-hot-encoding을 사용합니다. 이 추정기의 편리한 속성 중 하나는 교육이 필요하지 않다는 것입니다. 더욱이 데이터 양이 증가함에 따라 커널을 적절하게 좁히면 접근 방식이 일관됩니다(Mack and Silverman, 1982). 즉, 통계적으로 최적의 솔루션으로 수렴됩니다. 일부 커널을 검사하여 시작하겠습니다.
import numpy as np
import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l
d2l.use_svg_display()이 코드는 다음과 같은 작업을 수행합니다:
- numpy와 torch 라이브러리를 임포트합니다.
- torch.nn 내의 모듈들을 더 간단하게 접근하기 위해 nn 별칭을 사용합니다.
- torch.nn.functional 모듈 내의 함수들을 더 간단하게 접근하기 위해 F 별칭을 사용합니다.
- d2l 라이브러리 내의 torch 모듈을 d2l 별칭으로 사용합니다.
- d2l.use_svg_display()를 호출하여 그림을 SVG 형식으로 보여주는 설정을 적용합니다.
이 코드는 이후 코드에서 d2l 라이브러리를 사용할 준비를 하는 과정입니다.
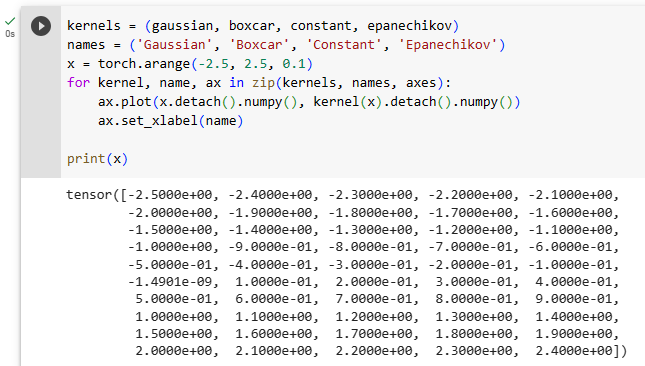
11.2.1. Kernels and Data
All the kernels α(k,q) defined in this section are translation and rotation invariant, that is, if we shift and rotate k and q in the same manner, the value of α remains unchanged. For simplicity we thus pick scalar arguments k,q∈ℝ and pick the key k=0 as the origin. This yields:
이 섹션에서 정의된 모든 커널 α(k,q)는 이동 및 회전 불변(translation and rotation invariant)입니다. 즉, k와 q를 같은 방식으로 이동하고 회전하면 α의 값은 변경되지 않습니다. 간단하게 하기 위해 스칼라 인수 k,q∈ℝ를 선택하고 키 k=0을 원점으로 선택합니다. 결과는 다음과 같습니다.
fig, axes = d2l.plt.subplots(1, 4, sharey=True, figsize=(12, 3))
# Define some kernels
def gaussian(x):
return torch.exp(-x**2 / 2)
def boxcar(x):
return torch.abs(x) < 1.0
def constant(x):
return 1.0 + 0 * x
def epanechikov(x):
return torch.max(1 - torch.abs(x), torch.zeros_like(x))이 코드는 다음과 같은 작업을 수행합니다:
- d2l.plt.subplots(1, 4, sharey=True, figsize=(12, 3))를 호출하여 1행 4열의 서브플롯을 생성합니다. 각각의 서브플롯은 공유된 y축을 가지며, 전체 그림의 크기는 (12, 3)로 설정됩니다.
- 네 가지 서로 다른 커널 함수 gaussian, boxcar, constant, epanechikov를 정의합니다. 이러한 커널 함수는 주어진 입력 x에 따라 값을 계산하며, 각각 가우시안, 박스카, 상수, epanechnikov 커널을 나타냅니다.
이 코드는 후속 코드에서 커널 함수를 사용하여 그림을 생성하는 일부 예제를 준비하는 과정입니다.

kernels = (gaussian, boxcar, constant, epanechikov)
names = ('Gaussian', 'Boxcar', 'Constant', 'Epanechikov')
x = torch.arange(-2.5, 2.5, 0.1)
for kernel, name, ax in zip(kernels, names, axes):
ax.plot(x.detach().numpy(), kernel(x).detach().numpy())
ax.set_xlabel(name)이 코드는 다음과 같은 작업을 수행합니다:
- kernels = (gaussian, boxcar, constant, epanechikov)을 사용하여 앞서 정의한 네 가지 커널 함수를 리스트로 정의합니다.
- names = ('Gaussian', 'Boxcar', 'Constant', 'Epanechikov')를 사용하여 각 커널 함수의 이름을 리스트로 정의합니다.
- x = torch.arange(-2.5, 2.5, 0.1)를 호출하여 범위 -2.5부터 2.5까지 0.1 간격으로 값을 가지는 벡터 x를 생성합니다.
- for kernel, name, ax in zip(kernels, names, axes): 루프를 통해 각각의 커널 함수와 해당 이름, 서브플롯 ax에 대해 다음 작업을 반복합니다:
- ax.plot(x.detach().numpy(), kernel(x).detach().numpy())를 호출하여 x 벡터를 입력으로 사용하여 해당 커널 함수를 계산한 결과를 그래프로 그립니다.
- ax.set_xlabel(name)을 사용하여 현재 서브플롯에 x축 레이블로 해당 커널 함수의 이름을 설정합니다.
즉, 이 코드는 네 가지 다른 형태의 커널 함수의 그래프를 생성하고, 각 그래프에 해당 커널 함수의 이름을 x축 레이블로 추가하는 작업을 수행합니다.
Pytorch에서 Tensor란?
PyTorch에서의 "Tensor"는 다차원 배열을 나타내는 기본적인 데이터 구조입니다. 텐서는 NumPy 배열과 유사하지만, GPU를 활용한 가속 연산을 지원하고, 자동 미분을 통한 그래디언트 계산을 위한 기능도 내장하고 있습니다.
텐서는 PyTorch의 핵심 데이터 타입 중 하나로, 다양한 수학 연산과 행렬 연산을 수행하며, 딥러닝 모델의 입력 데이터, 가중치, 출력 데이터 등을 나타내는 데 사용됩니다. 텐서는 다양한 차원(Dimension)을 가질 수 있으며, 이를 통해 스칼라, 벡터, 행렬, 다차원 행렬 등을 나타낼 수 있습니다.
텐서의 중요한 특징은 그래디언트(Gradient) 계산을 자동으로 수행할 수 있다는 점입니다. 이는 머신러닝 모델의 역전파(Backpropagation) 알고리즘에서 매우 중요한 역할을 합니다.
PyTorch에서는 텐서를 생성하고 조작하기 위해 다양한 함수와 연산을 제공하며, 이를 통해 딥러닝 모델을 구축하고 학습시키는 데 활용할 수 있습니다.
Different kernels correspond to different notions of range and smoothness. For instance, the boxcar kernel only attends to observations within a distance of 1 (or some otherwise defined hyperparameter) and does so indiscriminately.
서로 다른 커널은 range 와 smoothness의 서로 다른 개념에 상응합니다. 예를 들어 boxcar 커널은 distance 1(or some otherwise defined hyperparameter) 내의 관측값에만 주의를 기울이고 무차별적으로 수행합니다.
To see Nadaraya-Watson estimation in action, let’s define some training data. In the following we use the dependency where ϵ is drawn from a normal distribution with zero mean and unit variance.
Nadaraya-Watson 추정이 실제로 작동하는지 확인하기 위해 몇 가지 학습 데이터를 정의해 보겠습니다. 다음에서는 ϵ가 평균이 0(zero mean)이고 unit variance이 있는 정규 분포(normal distribution)에서 도출되는 종속성(dependency )을 사용합니다.

We draw 40 training examples.
def f(x):
return 2 * torch.sin(x) + x
n = 40
x_train, _ = torch.sort(torch.rand(n) * 5)
y_train = f(x_train) + torch.randn(n)
x_val = torch.arange(0, 5, 0.1)
y_val = f(x_val)
이 코드는 다음과 같은 작업을 수행합니다:
- def f(x):를 사용하여 함수 f를 정의합니다. 이 함수는 주어진 입력 x에 대해 2 * sin(x) + x를 계산하여 반환합니다.
- n = 40를 사용하여 학습 데이터의 수를 지정합니다.
- x_train, _ = torch.sort(torch.rand(n) * 5)를 호출하여 0과 5 사이에서 균일한 분포의 난수를 생성하고, 이를 정렬하여 학습 데이터 x_train을 생성합니다.
- y_train = f(x_train) + torch.randn(n)를 호출하여 학습 데이터 x_train에 함수 f를 적용한 결과에 노이즈를 추가하여 학습 데이터 y_train을 생성합니다.
- x_val = torch.arange(0, 5, 0.1)를 호출하여 0부터 5까지 0.1 간격으로 값을 가지는 벡터 x_val을 생성합니다.
- y_val = f(x_val)를 호출하여 벡터 x_val에 함수 f를 적용한 결과를 검증 데이터 y_val로 생성합니다.
즉, 이 코드는 주어진 함수 f에 노이즈를 추가하여 학습 데이터를 생성하고, 함수 f를 적용한 결과를 검증 데이터로 생성하는 작업을 수행합니다.

11.2.2. Attention Pooling via Nadaraya-Watson Regression
Now that we have data and kernels, all we need is a function that computes the kernel regression estimates. Note that we also want to obtain the relative kernel weights in order to perform some minor diagnostics. Hence we first compute the kernel between all training features (covariates) x_train and all validation features x_val. This yields a matrix, which we subsequently normalize. When multiplied with the training labels y_train we obtain the estimates.
이제 데이터와 커널이 있으므로 kernel regression estimates을 계산하는 함수만 있으면 됩니다. 우리는 또한 몇 가지 minor diagnostics을 수행하기 위해 상대적인 커널 가중치(relative kernel weights)를 얻고자 합니다. 따라서 먼저 모든 training features(공변량) x_train과 모든 alidation features x_val 사이의 커널을 계산합니다. 이것은 우리가 나중에 정규화하는 행렬을 생성합니다. 학습 레이블 y_train을 곱하면 추정치를 얻습니다.
Recall attention pooling in (11.1.1). Let each validation feature be a query, and each training feature-label pair be a key-value pair. As a result, the normalized relative kernel weights (attention_w below) are the attention weights.
(11.1.1)의 attention pooling을 상기하십시오. 각 validation feature을 쿼리로 만들고 각 training feature-label pair 을 key-value pair로 설정합니다. 결과적으로 정규화된 relative kernel weights(아래의 attention_w)가 attention weights입니다.
def nadaraya_watson(x_train, y_train, x_val, kernel):
dists = x_train.reshape((-1, 1)) - x_val.reshape((1, -1))
# Each column/row corresponds to each query/key
k = kernel(dists).type(torch.float32)
# Normalization over keys for each query
attention_w = k / k.sum(0)
y_hat = y_train@attention_w
return y_hat, attention_w
위 코드는 Nadaraya-Watson 커널 회귀를 구현한 함수입니다. Nadaraya-Watson 커널 회귀는 비선형 회귀 문제를 해결하기 위한 방법 중 하나로, 주어진 입력 데이터와 해당 입력 데이터에 대한 목표값을 이용하여 예측 모델을 만드는 알고리즘입니다.
함수의 입력으로는 x_train과 y_train은 학습 데이터의 입력 특징과 목표값을 나타내는 텐서입니다. x_val은 예측을 수행할 때의 입력 특징값을 나타내며, kernel은 사용할 커널 함수입니다.
커널 함수를 사용하여 입력 데이터와 예측 데이터 사이의 거리를 계산하고, 그 거리를 기반으로 각 입력 데이터의 가중치를 계산합니다. 이렇게 계산된 가중치를 이용하여 예측값을 계산하고 반환합니다.
이 함수를 통해 Nadaraya-Watson 커널 회귀를 수행하여 입력 데이터에 대한 예측값을 얻을 수 있습니다.
- nadaraya_watson 함수를 정의합니다. 이 함수는 Nadaraya-Watson 커널 회귀를 구현하는 함수입니다.
- x_train: 학습 데이터의 입력 특징을 나타내는 텐서입니다.
- y_train: 학습 데이터의 목표값(출력값)을 나타내는 텐서입니다.
- x_val: 예측을 수행할 때의 입력 특징값을 나타내는 텐서입니다.
- kernel: 사용할 커널 함수를 나타내는 함수입니다.
- dists는 입력 데이터와 예측 데이터 사이의 거리를 계산한 텐서입니다.
- x_train을 (n, 1) 모양으로 재구성하고 x_val을 (1, m) 모양으로 재구성한 후 뺄셈을 수행하여 거리를 계산합니다. 이렇게 하면 모든 입력 데이터와 예측 데이터 사이의 거리가 계산됩니다.
- kernel 함수를 사용하여 거리 텐서에 커널 함수를 적용하여 커널 행렬 k를 생성합니다.
- .type(torch.float32)를 사용하여 결과를 32비트 부동 소수점형 텐서로 변환합니다.
- k 행렬의 열별 합을 계산한 후, 각 원소를 열별 합으로 나누어 각 입력 데이터에 대한 가중치를 계산합니다.
- 이렇게 하면 입력 데이터에 대한 가중치 행렬 attention_w가 생성됩니다.
- 목표값 y_train과 가중치 행렬 attention_w의 내적을 계산하여 예측값 y_hat을 구합니다.
- 이렇게 하면 각 예측 데이터에 대한 예측값이 얻어집니다.
- 계산된 예측값 y_hat과 가중치 행렬 attention_w를 반환합니다.
- y_hat은 입력 데이터 x_val에 대한 예측 결과를 나타냅니다.
- attention_w는 각 입력 데이터의 가중치를 나타냅니다.
참고로 아래는 가우시안 커널을 써서 Attention Weights를 얻어내고 이 Attention Weights를 사용해서 목표값 y_train에 대한 예측값 y_hat을 가하는 과정을 테스트 해 봤습니다.

====Start dists =====
tensor([[ 0.5508, 0.4508, 0.3508, ..., -4.1492, -4.2492, -4.3492],
[ 0.6583, 0.5583, 0.4583, ..., -4.0417, -4.1417, -4.2417],
[ 0.7619, 0.6619, 0.5619, ..., -3.9381, -4.0381, -4.1381],
...,
[ 4.6253, 4.5253, 4.4253, ..., -0.0747, -0.1747, -0.2747],
[ 4.8496, 4.7496, 4.6496, ..., 0.1496, 0.0496, -0.0504],
[ 4.9156, 4.8156, 4.7156, ..., 0.2156, 0.1156, 0.0156]])
====End dists=====
====Start k =====
tensor([[8.5925e-01, 9.0338e-01, 9.4032e-01, ..., 1.8265e-04, 1.2002e-04,
7.8081e-05],
[8.0520e-01, 8.5569e-01, 9.0031e-01, ..., 2.8366e-04, 1.8841e-04,
1.2390e-04],
[7.4810e-01, 8.0329e-01, 8.5398e-01, ..., 4.2883e-04, 2.8780e-04,
1.9122e-04],
...,
[2.2622e-05, 3.5747e-05, 5.5924e-05, ..., 9.9721e-01, 9.8485e-01,
9.6297e-01],
[7.8152e-06, 1.2630e-05, 2.0206e-05, ..., 9.8887e-01, 9.9877e-01,
9.9873e-01],
[5.6628e-06, 9.2117e-06, 1.4836e-05, ..., 9.7702e-01, 9.9334e-01,
9.9988e-01]])
====End k=====
====Start attention_w =====
tensor([[1.2736e-01, 1.1960e-01, 1.1196e-01, ..., 1.3661e-05, 9.5400e-06,
6.6333e-06],
[1.1934e-01, 1.1328e-01, 1.0720e-01, ..., 2.1215e-05, 1.4976e-05,
1.0526e-05],
[1.1088e-01, 1.0635e-01, 1.0168e-01, ..., 3.2072e-05, 2.2876e-05,
1.6245e-05],
...,
[3.3530e-06, 4.7324e-06, 6.6587e-06, ..., 7.4582e-02, 7.8282e-02,
8.1809e-02],
[1.1584e-06, 1.6720e-06, 2.4059e-06, ..., 7.3958e-02, 7.9389e-02,
8.4847e-02],
[8.3933e-07, 1.2195e-06, 1.7664e-06, ..., 7.3072e-02, 7.8957e-02,
8.4945e-02]])
====End attention_w=====
====Start y_hat =====
tensor([2.6607, 2.6860, 2.7113, 2.7365, 2.7617, 2.7866, 2.8113, 2.8357, 2.8596,
2.8829, 2.9055, 2.9273, 2.9483, 2.9681, 2.9868, 3.0042, 3.0202, 3.0346,
3.0474, 3.0585, 3.0678, 3.0753, 3.0810, 3.0848, 3.0868, 3.0872, 3.0859,
3.0832, 3.0793, 3.0743, 3.0686, 3.0624, 3.0559, 3.0495, 3.0435, 3.0382,
3.0337, 3.0305, 3.0286, 3.0283, 3.0296, 3.0327, 3.0376, 3.0443, 3.0527,
3.0629, 3.0747, 3.0880, 3.1027, 3.1186])
====End y_hat=====
Let’s have a look at the kind of estimates that the different kernels produce.
서로 다른 커널이 생성하는 추정의 종류를 살펴보겠습니다.
def plot(x_train, y_train, x_val, y_val, kernels, names, attention=False):
fig, axes = d2l.plt.subplots(1, 4, sharey=True, figsize=(12, 3))
for kernel, name, ax in zip(kernels, names, axes):
y_hat, attention_w = nadaraya_watson(x_train, y_train, x_val, kernel)
if attention:
pcm = ax.imshow(attention_w.detach().numpy(), cmap='Reds')
else:
ax.plot(x_val, y_hat)
ax.plot(x_val, y_val, 'm--')
ax.plot(x_train, y_train, 'o', alpha=0.5);
ax.set_xlabel(name)
if not attention:
ax.legend(['y_hat', 'y'])
if attention:
fig.colorbar(pcm, ax=axes, shrink=0.7)
plot(x_train, y_train, x_val, y_val, kernels, names)
- plot 함수를 정의합니다. 이 함수는 데이터와 커널 함수들을 사용하여 데이터 포인트들을 예측하고 시각화하는 역할을 합니다.
- x_train: 학습 데이터의 입력 특징을 나타내는 텐서입니다.
- y_train: 학습 데이터의 목표값(출력값)을 나타내는 텐서입니다.
- x_val: 예측을 수행할 때의 입력 특징값을 나타내는 텐서입니다.
- y_val: 예측 결과와 비교할 실제 목표값을 나타내는 텐서입니다.
- kernels: 사용할 커널 함수들을 담은 튜플 또는 리스트입니다.
- names: 각 커널 함수들의 이름을 담은 튜플 또는 리스트입니다.
- attention: 가중치 히트맵을 표시할지 여부를 결정하는 불리언 값입니다.
fig, axes = d2l.plt.subplots(1, 4, sharey=True, figsize=(12, 3))- 1행 4열의 서브플롯들을 생성합니다. 이 서브플롯들은 커널 함수별 결과를 시각화하기 위해 사용됩니다.
- sharey=True로 설정하여 모든 서브플롯의 y축을 공유합니다.
- figsize=(12, 3)로 설정하여 전체 그림의 크기를 지정합니다.
for kernel, name, ax in zip(kernels, names, axes):- kernels와 names의 원소를 순서대로 묶어서 반복문을 수행합니다.
- kernel: 현재 반복문에서 사용될 커널 함수입니다.
- name: 해당 커널 함수의 이름입니다.
- ax: 현재 서브플롯을 가리키는 객체입니다.
y_hat, attention_w = nadaraya_watson(x_train, y_train, x_val, kernel)- 현재 커널 함수 kernel을 사용하여 Nadaraya-Watson 예측을 수행합니다.
- nadaraya_watson 함수는 x_train, y_train, x_val, kernel을 인자로 받아 예측 결과 y_hat과 가중치 attention_w를 반환합니다.
if attention:
pcm = ax.imshow(attention_w.detach().numpy(), cmap='Reds')
else:
ax.plot(x_val, y_hat)
ax.plot(x_val, y_val, 'm--')
ax.plot(x_train, y_train, 'o', alpha=0.5);
ax.set_xlabel(name)
if not attention:
ax.legend(['y_hat', 'y'])- 만약 attention이 True라면, 가중치 히트맵을 시각화합니다.
- 그렇지 않으면 예측 결과 y_hat과 실제 목표값 y_val을 선 그래프로 시각화합니다.
- 학습 데이터 x_train과 y_train을 점으로 나타냅니다.
- ax.set_xlabel(name)로 x축의 레이블을 현재 커널 함수의 이름으로 설정합니다.
- not attention 조건에서는 범례를 추가합니다.
if attention:
fig.colorbar(pcm, ax=axes, shrink=0.7)만약 attention이 True라면, 가중치 히트맵에 컬러바를 추가합니다.
plot(x_train, y_train, x_val, y_val, kernels, names)plot 함수를 호출하여 실제 데이터와 커널 함수들로 예측 결과를 시각화합니다.

참고로 각 Kernal 별로 dists, k, attention_w, y_hat을 출력한 결과는 아래와 같습니다.
====Gaussian =====
====Start dists =====
tensor([[ 0.5508, 0.4508, 0.3508, ..., -4.1492, -4.2492, -4.3492],
[ 0.6583, 0.5583, 0.4583, ..., -4.0417, -4.1417, -4.2417],
[ 0.7619, 0.6619, 0.5619, ..., -3.9381, -4.0381, -4.1381],
...,
[ 4.6253, 4.5253, 4.4253, ..., -0.0747, -0.1747, -0.2747],
[ 4.8496, 4.7496, 4.6496, ..., 0.1496, 0.0496, -0.0504],
[ 4.9156, 4.8156, 4.7156, ..., 0.2156, 0.1156, 0.0156]])
====End dists=====
====Start k =====
tensor([[8.5925e-01, 9.0338e-01, 9.4032e-01, ..., 1.8265e-04, 1.2002e-04,
7.8081e-05],
[8.0520e-01, 8.5569e-01, 9.0031e-01, ..., 2.8366e-04, 1.8841e-04,
1.2390e-04],
[7.4810e-01, 8.0329e-01, 8.5398e-01, ..., 4.2883e-04, 2.8780e-04,
1.9122e-04],
...,
[2.2622e-05, 3.5747e-05, 5.5924e-05, ..., 9.9721e-01, 9.8485e-01,
9.6297e-01],
[7.8152e-06, 1.2630e-05, 2.0206e-05, ..., 9.8887e-01, 9.9877e-01,
9.9873e-01],
[5.6628e-06, 9.2117e-06, 1.4836e-05, ..., 9.7702e-01, 9.9334e-01,
9.9988e-01]])
====End k=====
====Start attention_w =====
tensor([[1.2736e-01, 1.1960e-01, 1.1196e-01, ..., 1.3661e-05, 9.5400e-06,
6.6333e-06],
[1.1934e-01, 1.1328e-01, 1.0720e-01, ..., 2.1215e-05, 1.4976e-05,
1.0526e-05],
[1.1088e-01, 1.0635e-01, 1.0168e-01, ..., 3.2072e-05, 2.2876e-05,
1.6245e-05],
...,
[3.3530e-06, 4.7324e-06, 6.6587e-06, ..., 7.4582e-02, 7.8282e-02,
8.1809e-02],
[1.1584e-06, 1.6720e-06, 2.4059e-06, ..., 7.3958e-02, 7.9389e-02,
8.4847e-02],
[8.3933e-07, 1.2195e-06, 1.7664e-06, ..., 7.3072e-02, 7.8957e-02,
8.4945e-02]])
====End attention_w=====
====Start y_hat =====
tensor([2.6607, 2.6860, 2.7113, 2.7365, 2.7617, 2.7866, 2.8113, 2.8357, 2.8596,
2.8829, 2.9055, 2.9273, 2.9483, 2.9681, 2.9868, 3.0042, 3.0202, 3.0346,
3.0474, 3.0585, 3.0678, 3.0753, 3.0810, 3.0848, 3.0868, 3.0872, 3.0859,
3.0832, 3.0793, 3.0743, 3.0686, 3.0624, 3.0559, 3.0495, 3.0435, 3.0382,
3.0337, 3.0305, 3.0286, 3.0283, 3.0296, 3.0327, 3.0376, 3.0443, 3.0527,
3.0629, 3.0747, 3.0880, 3.1027, 3.1186])
====End y_hat=====
====Boxcar =====
====Start dists =====
tensor([[ 0.5508, 0.4508, 0.3508, ..., -4.1492, -4.2492, -4.3492],
[ 0.6583, 0.5583, 0.4583, ..., -4.0417, -4.1417, -4.2417],
[ 0.7619, 0.6619, 0.5619, ..., -3.9381, -4.0381, -4.1381],
...,
[ 4.6253, 4.5253, 4.4253, ..., -0.0747, -0.1747, -0.2747],
[ 4.8496, 4.7496, 4.6496, ..., 0.1496, 0.0496, -0.0504],
[ 4.9156, 4.8156, 4.7156, ..., 0.2156, 0.1156, 0.0156]])
====End dists=====
====Start k =====
tensor([[1., 1., 1., ..., 0., 0., 0.],
[1., 1., 1., ..., 0., 0., 0.],
[1., 1., 1., ..., 0., 0., 0.],
...,
[0., 0., 0., ..., 1., 1., 1.],
[0., 0., 0., ..., 1., 1., 1.],
[0., 0., 0., ..., 1., 1., 1.]])
====End k=====
====Start attention_w =====
tensor([[0.2000, 0.2000, 0.1667, ..., 0.0000, 0.0000, 0.0000],
[0.2000, 0.2000, 0.1667, ..., 0.0000, 0.0000, 0.0000],
[0.2000, 0.2000, 0.1667, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.1000, 0.1000, 0.1000],
[0.0000, 0.0000, 0.0000, ..., 0.1000, 0.1000, 0.1000],
[0.0000, 0.0000, 0.0000, ..., 0.1000, 0.1000, 0.1000]])
====End attention_w=====
====Start y_hat =====
tensor([2.2189, 2.2189, 2.5463, 2.5463, 2.5886, 2.5886, 2.5653, 2.5653, 2.8933,
2.8457, 2.8415, 2.8415, 2.8415, 2.8946, 2.8946, 2.9729, 3.1067, 3.1691,
3.1108, 3.1701, 3.1734, 3.1363, 3.1449, 3.1449, 3.1601, 3.0892, 3.1856,
3.2215, 3.0757, 3.1402, 3.1640, 3.1863, 3.0839, 3.0560, 2.9216, 2.8161,
2.8289, 2.8890, 2.9115, 2.8865, 3.0837, 3.1271, 3.0312, 3.0312, 3.0312,
3.1445, 3.1445, 3.0645, 3.0645, 3.0645])
====End y_hat=====
====Constant =====
====Start dists =====
tensor([[ 0.5508, 0.4508, 0.3508, ..., -4.1492, -4.2492, -4.3492],
[ 0.6583, 0.5583, 0.4583, ..., -4.0417, -4.1417, -4.2417],
[ 0.7619, 0.6619, 0.5619, ..., -3.9381, -4.0381, -4.1381],
...,
[ 4.6253, 4.5253, 4.4253, ..., -0.0747, -0.1747, -0.2747],
[ 4.8496, 4.7496, 4.6496, ..., 0.1496, 0.0496, -0.0504],
[ 4.9156, 4.8156, 4.7156, ..., 0.2156, 0.1156, 0.0156]])
====End dists=====
====Epanechikov =====
====Start k =====
tensor([[1., 1., 1., ..., 1., 1., 1.],
[1., 1., 1., ..., 1., 1., 1.],
[1., 1., 1., ..., 1., 1., 1.],
...,
[1., 1., 1., ..., 1., 1., 1.],
[1., 1., 1., ..., 1., 1., 1.],
[1., 1., 1., ..., 1., 1., 1.]])
====End k=====
====Start attention_w =====
tensor([[0.0250, 0.0250, 0.0250, ..., 0.0250, 0.0250, 0.0250],
[0.0250, 0.0250, 0.0250, ..., 0.0250, 0.0250, 0.0250],
[0.0250, 0.0250, 0.0250, ..., 0.0250, 0.0250, 0.0250],
...,
[0.0250, 0.0250, 0.0250, ..., 0.0250, 0.0250, 0.0250],
[0.0250, 0.0250, 0.0250, ..., 0.0250, 0.0250, 0.0250],
[0.0250, 0.0250, 0.0250, ..., 0.0250, 0.0250, 0.0250]])
====End attention_w=====
====Start y_hat =====
tensor([3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182,
3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182,
3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182,
3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182,
3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182, 3.0182,
3.0182, 3.0182, 3.0182, 3.0182, 3.0182])
====End y_hat=====
====Start dists =====
tensor([[ 0.5508, 0.4508, 0.3508, ..., -4.1492, -4.2492, -4.3492],
[ 0.6583, 0.5583, 0.4583, ..., -4.0417, -4.1417, -4.2417],
[ 0.7619, 0.6619, 0.5619, ..., -3.9381, -4.0381, -4.1381],
...,
[ 4.6253, 4.5253, 4.4253, ..., -0.0747, -0.1747, -0.2747],
[ 4.8496, 4.7496, 4.6496, ..., 0.1496, 0.0496, -0.0504],
[ 4.9156, 4.8156, 4.7156, ..., 0.2156, 0.1156, 0.0156]])
====End dists=====
====Start k =====
tensor([[0.4492, 0.5492, 0.6492, ..., 0.0000, 0.0000, 0.0000],
[0.3417, 0.4417, 0.5417, ..., 0.0000, 0.0000, 0.0000],
[0.2381, 0.3381, 0.4381, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.9253, 0.8253, 0.7253],
[0.0000, 0.0000, 0.0000, ..., 0.8504, 0.9504, 0.9496],
[0.0000, 0.0000, 0.0000, ..., 0.7844, 0.8844, 0.9844]])
====End k=====
====Start attention_w =====
tensor([[0.4024, 0.3398, 0.2957, ..., 0.0000, 0.0000, 0.0000],
[0.3061, 0.2733, 0.2468, ..., 0.0000, 0.0000, 0.0000],
[0.2133, 0.2092, 0.1996, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.1284, 0.1249, 0.1228],
[0.0000, 0.0000, 0.0000, ..., 0.1180, 0.1439, 0.1608],
[0.0000, 0.0000, 0.0000, ..., 0.1089, 0.1339, 0.1667]])
====End attention_w=====
====Start y_hat =====
tensor([1.9447, 2.0295, 2.1500, 2.2351, 2.2972, 2.3465, 2.4159, 2.5066, 2.5946,
2.6895, 2.7616, 2.8446, 2.8938, 2.9361, 2.9805, 3.0347, 3.0817, 3.1408,
3.1729, 3.1868, 3.2161, 3.2179, 3.2272, 3.2436, 3.2568, 3.2407, 3.2075,
3.1608, 3.1310, 3.1068, 3.0765, 3.0740, 3.0586, 3.0188, 2.9681, 2.9304,
2.8993, 2.8635, 2.8215, 2.7971, 2.8086, 2.8105, 2.8310, 2.8737, 2.9313,
3.0022, 3.0951, 3.1819, 3.2772, 3.3859])
====End y_hat=====
The first thing that stands out is that all three nontrivial kernels (Gaussian, Boxcar, and Epanechikov) produce fairly workable estimates that are not too far from the true function. Only the constant kernel that leads to the trivial estimate f(x)=1/n∑iyi produces a rather unrealistic result. Let’s inspect the attention weighting a bit more closely:
가장 먼저 눈에 띄는 것은 3개의 중요한(nontrivial ) 커널(Gaussian, Boxcar 및 Epanechikov) 모두 실제 함수에서 그리 멀지 않은 상당히 실행 가능한 추정치를 생성한다는 것입니다. 사소한(trivial ) 추정치 f(x)=1/n∑iyi로 이어지는 상수 커널만이 다소 비현실적인 결과를 생성합니다. 어텐션 가중치를 좀 더 자세히 살펴보겠습니다.
plot(x_train, y_train, x_val, y_val, kernels, names, attention=True)해당 코드는 주어진 데이터와 커널 함수를 사용하여 Nadaraya-Watson 예측 결과 및 가중치 히트맵을 시각화하는 함수를 호출하는 코드입니다.
- x_train, y_train: 학습 데이터의 입력 특징과 목표값입니다.
- x_val, y_val: 예측을 수행할 때 사용할 입력 특징과 실제 목표값입니다.
- kernels: 사용할 커널 함수들을 담은 튜플 또는 리스트입니다.
- names: 각 커널 함수들의 이름을 담은 튜플 또는 리스트입니다.
- attention=True: 가중치 히트맵을 표시하도록 설정합니다.
즉, 이 코드는 plot 함수를 호출하여 주어진 데이터와 커널 함수들을 이용하여 Nadaraya-Watson 예측 결과와 가중치 히트맵을 가시화하는 작업을 수행합니다.
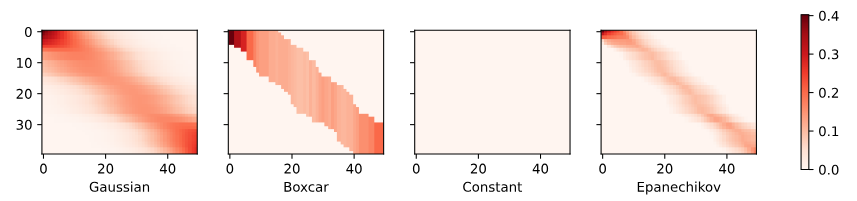
The visualization clearly shows why the estimates for Gaussian, Boxcar, and Epanechikov are very similar: after all, they are derived from very similar attention weights, despite the different functional form of the kernel. This raises the question as to whether this is always the case.
시각화는 Gaussian, Boxcar 및 Epanechikov에 대한 추정치가 매우 유사한 이유를 명확하게 보여줍니다. 결국 이들은 커널의 다른 기능적 형태에도 불구하고 매우 유사한 attention weights에서 파생됩니다. 이것은 이것이 항상 사실인지에 대한 질문을 제기합니다.
11.2.3. Adapting Attention Pooling
We could replace the Gaussian kernel with one of a different width. That is, we could use α(q,k)=exp(−1/2σ2‖q−k‖2) where σ2 determines the width of the kernel. Let’s see whether this affects the outcomes.
Gaussian kernel을 다른 width 중 하나로 교체할 수 있습니다. 즉, α(q,k)=exp(−1/2σ**2‖q−k‖**2)를 사용할 수 있습니다. 여기서 σ2는 커널의 너비를 결정합니다. 이것이 결과에 영향을 미치는지 봅시다.
sigmas = (0.1, 0.2, 0.5, 1)
names = ['Sigma ' + str(sigma) for sigma in sigmas]
def gaussian_with_width(sigma):
return (lambda x: torch.exp(-x**2 / (2*sigma**2)))
kernels = [gaussian_with_width(sigma) for sigma in sigmas]
plot(x_train, y_train, x_val, y_val, kernels, names)
위 코드는 주어진 각각의 시그마 값에 대한 가우시안 커널을 생성하고, 이를 사용하여 Nadaraya-Watson 예측 결과를 가시화하는 작업을 수행합니다.
- sigmas: 가우시안 커널을 생성할 때 사용할 시그마 값들을 담은 튜플 또는 리스트입니다.
- names: 각 시그마 값에 대한 이름을 담은 리스트입니다.
- gaussian_with_width(sigma): 주어진 시그마 값을 사용하여 가우시안 커널 함수를 생성하는 람다 함수입니다. 가우시안 커널의 폭은 시그마 값에 따라 결정됩니다.
- kernels: 시그마 값에 따라 생성한 가우시안 커널 함수들을 담은 리스트입니다.
따라서 위 코드는 생성한 가우시안 커널들과 주어진 데이터를 사용하여 Nadaraya-Watson 예측 결과를 시각화합니다. 이때 시그마 값이 작을수록 커널의 폭이 좁아지므로 예측 결과가 주변 데이터에 민감하게 반응하게 됩니다.
sigmas = (0.1, 0.2, 0.5, 1)sigmas: 시그마 값을 나타내는 튜플 또는 리스트로, 가우시안 커널을 생성할 때 사용할 다양한 시그마 값을 포함합니다.
names = ['Sigma ' + str(sigma) for sigma in sigmas]names: 시그마 값에 대응하는 이름을 가진 리스트로, 각 시그마 값에 대한 설명을 제공하기 위해 생성됩니다.
def gaussian_with_width(sigma):
return (lambda x: torch.exp(-x**2 / (2*sigma**2)))gaussian_with_width(sigma): 주어진 시그마 값을 사용하여 가우시안 커널 함수를 생성하는 람다 함수입니다. 커널 함수는 입력 x에 대해 가우시안 분포 형태로 값을 반환합니다. 시그마 값이 작을수록 함수의 폭이 좁아지게 됩니다.
kernels = [gaussian_with_width(sigma) for sigma in sigmas]kernels: 시그마 값들에 대응하는 가우시안 커널 함수들을 리스트에 저장합니다. 각 시그마 값에 해당하는 커널 함수가 생성됩니다.
plot(x_train, y_train, x_val, y_val, kernels, names)plot: 앞서 정의한 커널 함수들과 데이터를 사용하여 Nadaraya-Watson 예측 결과를 시각화하는 함수입니다. x_train과 y_train은 훈련 데이터, x_val과 y_val은 검증 데이터를 나타냅니다. kernels와 names는 위에서 생성한 커널 함수들과 그에 대응하는 이름입니다.

참고로 이 때 nadaraya_watson(x_train, y_train, x_val, kernel) 함수를 거치면서 각 Sigma 별 dists, k, attention_w, y_hat 의 값들은 아래와 같습니다.
========== Sigma 0.1 ================
====Start dists =====
tensor([[ 0.5508, 0.4508, 0.3508, ..., -4.1492, -4.2492, -4.3492],
[ 0.6583, 0.5583, 0.4583, ..., -4.0417, -4.1417, -4.2417],
[ 0.7619, 0.6619, 0.5619, ..., -3.9381, -4.0381, -4.1381],
...,
[ 4.6253, 4.5253, 4.4253, ..., -0.0747, -0.1747, -0.2747],
[ 4.8496, 4.7496, 4.6496, ..., 0.1496, 0.0496, -0.0504],
[ 4.9156, 4.8156, 4.7156, ..., 0.2156, 0.1156, 0.0156]])
====End dists=====
====Start k =====
tensor([[2.5833e-07, 3.8647e-05, 2.1270e-03, ..., 0.0000e+00, 0.0000e+00,
0.0000e+00],
[3.8917e-10, 1.7056e-07, 2.7501e-05, ..., 0.0000e+00, 0.0000e+00,
0.0000e+00],
[2.4881e-13, 3.0724e-10, 1.3956e-07, ..., 0.0000e+00, 0.0000e+00,
0.0000e+00],
...,
[0.0000e+00, 0.0000e+00, 0.0000e+00, ..., 7.5638e-01, 2.1730e-01,
2.2965e-02],
[0.0000e+00, 0.0000e+00, 0.0000e+00, ..., 3.2648e-01, 8.8415e-01,
8.8084e-01],
[0.0000e+00, 0.0000e+00, 0.0000e+00, ..., 9.7849e-02, 5.1260e-01,
9.8789e-01]])
====End k=====
====Start attention_w =====
tensor([[9.9849e-01, 9.9560e-01, 9.8717e-01, ..., 0.0000e+00, 0.0000e+00,
0.0000e+00],
[1.5042e-03, 4.3940e-03, 1.2763e-02, ..., 0.0000e+00, 0.0000e+00,
0.0000e+00],
[9.6172e-07, 7.9148e-06, 6.4774e-05, ..., 0.0000e+00, 0.0000e+00,
0.0000e+00],
...,
[0.0000e+00, 0.0000e+00, 0.0000e+00, ..., 4.2353e-01, 1.2920e-01,
1.2120e-02],
[0.0000e+00, 0.0000e+00, 0.0000e+00, ..., 1.8281e-01, 5.2568e-01,
4.6487e-01],
[0.0000e+00, 0.0000e+00, 0.0000e+00, ..., 5.4790e-02, 3.0477e-01,
5.2137e-01]])
====End attention_w=====
====Start y_hat =====
tensor([0.7001, 0.7049, 0.7188, 0.7589, 0.8718, 1.1642, 1.7662, 2.5361, 2.9078,
2.6384, 2.6582, 3.2754, 3.6133, 3.0595, 2.7241, 2.5963, 2.8396, 3.4269,
3.4479, 3.0167, 2.7594, 3.0357, 3.3311, 3.5103, 3.8398, 3.9149, 3.4224,
3.2546, 3.1993, 2.9091, 2.8003, 3.0526, 3.4077, 3.0245, 2.0238, 2.5702,
3.2725, 3.4686, 3.4608, 3.1705, 2.8389, 2.4726, 2.0033, 1.9214, 2.3984,
2.7935, 3.2564, 3.8366, 4.2474, 4.5033])
====End y_hat=====
========== Sigma 0.2 ================
====Start dists =====
tensor([[ 0.5508, 0.4508, 0.3508, ..., -4.1492, -4.2492, -4.3492],
[ 0.6583, 0.5583, 0.4583, ..., -4.0417, -4.1417, -4.2417],
[ 0.7619, 0.6619, 0.5619, ..., -3.9381, -4.0381, -4.1381],
...,
[ 4.6253, 4.5253, 4.4253, ..., -0.0747, -0.1747, -0.2747],
[ 4.8496, 4.7496, 4.6496, ..., 0.1496, 0.0496, -0.0504],
[ 4.9156, 4.8156, 4.7156, ..., 0.2156, 0.1156, 0.0156]])
====End dists=====
====Start k =====
tensor([[2.2545e-02, 7.8846e-02, 2.1475e-01, ..., 0.0000e+00, 0.0000e+00,
0.0000e+00],
[4.4415e-03, 2.0322e-02, 7.2416e-02, ..., 0.0000e+00, 0.0000e+00,
0.0000e+00],
[7.0627e-04, 4.1867e-03, 1.9328e-02, ..., 0.0000e+00, 0.0000e+00,
0.0000e+00],
...,
[0.0000e+00, 0.0000e+00, 0.0000e+00, ..., 9.3258e-01, 6.8275e-01,
3.8929e-01],
[0.0000e+00, 0.0000e+00, 0.0000e+00, ..., 7.5590e-01, 9.6969e-01,
9.6878e-01],
[0.0000e+00, 0.0000e+00, 0.0000e+00, ..., 5.5929e-01, 8.4615e-01,
9.9696e-01]])
====End k=====
====Start attention_w =====
tensor([[0.8134, 0.7612, 0.6969, ..., 0.0000, 0.0000, 0.0000],
[0.1603, 0.1962, 0.2350, ..., 0.0000, 0.0000, 0.0000],
[0.0255, 0.0404, 0.0627, ..., 0.0000, 0.0000, 0.0000],
...,
[0.0000, 0.0000, 0.0000, ..., 0.1917, 0.1766, 0.1332],
[0.0000, 0.0000, 0.0000, ..., 0.1554, 0.2509, 0.3314],
[0.0000, 0.0000, 0.0000, ..., 0.1150, 0.2189, 0.3410]])
====End attention_w=====
====Start y_hat =====
tensor([1.0328, 1.1357, 1.2674, 1.4327, 1.6341, 1.8683, 2.1208, 2.3631, 2.5644,
2.7187, 2.8481, 2.9605, 3.0131, 2.9749, 2.9317, 2.9685, 3.0621, 3.1506,
3.1919, 3.1827, 3.1649, 3.2103, 3.3393, 3.4787, 3.5528, 3.5163, 3.3763,
3.2104, 3.0832, 3.0113, 2.9892, 2.9975, 3.0009, 2.9633, 2.9128, 2.9430,
3.0500, 3.1424, 3.1170, 2.9067, 2.6212, 2.4255, 2.3716, 2.4512, 2.6213,
2.8445, 3.1176, 3.4497, 3.8138, 4.1366])
====End y_hat=====
========== Sigma 0.5 ================
====Start dists =====
tensor([[ 0.5508, 0.4508, 0.3508, ..., -4.1492, -4.2492, -4.3492],
[ 0.6583, 0.5583, 0.4583, ..., -4.0417, -4.1417, -4.2417],
[ 0.7619, 0.6619, 0.5619, ..., -3.9381, -4.0381, -4.1381],
...,
[ 4.6253, 4.5253, 4.4253, ..., -0.0747, -0.1747, -0.2747],
[ 4.8496, 4.7496, 4.6496, ..., 0.1496, 0.0496, -0.0504],
[ 4.9156, 4.8156, 4.7156, ..., 0.2156, 0.1156, 0.0156]])
====End dists=====
====Start k =====
tensor([[5.4511e-01, 6.6602e-01, 7.8183e-01, ..., 1.1130e-15, 2.0750e-16,
3.7168e-17],
[4.2034e-01, 5.3614e-01, 6.5701e-01, ..., 6.4745e-15, 1.2601e-15,
2.3563e-16],
[3.1321e-01, 4.1639e-01, 5.3185e-01, ..., 3.3818e-14, 6.8602e-15,
1.3371e-15],
...,
[2.6191e-19, 1.6329e-18, 9.7812e-18, ..., 9.8889e-01, 9.4077e-01,
8.5989e-01],
[3.7305e-21, 2.5442e-20, 1.6671e-19, ..., 9.5621e-01, 9.9509e-01,
9.9494e-01],
[1.0283e-21, 7.2004e-21, 4.8442e-20, ..., 9.1122e-01, 9.7362e-01,
9.9951e-01]])
====End k=====
====Start attention_w =====
tensor([[3.1451e-01, 2.8984e-01, 2.6481e-01, ..., 1.2967e-16, 2.6479e-17,
5.3421e-18],
[2.4252e-01, 2.3332e-01, 2.2253e-01, ..., 7.5431e-16, 1.6080e-16,
3.3866e-17],
[1.8071e-01, 1.8121e-01, 1.8014e-01, ..., 3.9400e-15, 8.7542e-16,
1.9217e-16],
...,
[1.5111e-19, 7.1061e-19, 3.3129e-18, ..., 1.1521e-01, 1.2005e-01,
1.2359e-01],
[2.1524e-21, 1.1072e-20, 5.6464e-20, ..., 1.1140e-01, 1.2698e-01,
1.4300e-01],
[5.9329e-22, 3.1335e-21, 1.6408e-20, ..., 1.0616e-01, 1.2424e-01,
1.4366e-01]])
====End attention_w=====
====Start y_hat =====
tensor([2.1311, 2.1903, 2.2514, 2.3142, 2.3788, 2.4450, 2.5123, 2.5803, 2.6482,
2.7151, 2.7796, 2.8407, 2.8973, 2.9488, 2.9951, 3.0365, 3.0735, 3.1069,
3.1370, 3.1638, 3.1868, 3.2048, 3.2164, 3.2204, 3.2161, 3.2039, 3.1852,
3.1620, 3.1366, 3.1105, 3.0848, 3.0598, 3.0354, 3.0106, 2.9846, 2.9568,
2.9273, 2.8980, 2.8722, 2.8540, 2.8474, 2.8547, 2.8767, 2.9125, 2.9606,
3.0188, 3.0852, 3.1581, 3.2357, 3.3168])
====End y_hat=====
========== Sigma 1 ================
====Start dists =====
tensor([[ 0.5508, 0.4508, 0.3508, ..., -4.1492, -4.2492, -4.3492],
[ 0.6583, 0.5583, 0.4583, ..., -4.0417, -4.1417, -4.2417],
[ 0.7619, 0.6619, 0.5619, ..., -3.9381, -4.0381, -4.1381],
...,
[ 4.6253, 4.5253, 4.4253, ..., -0.0747, -0.1747, -0.2747],
[ 4.8496, 4.7496, 4.6496, ..., 0.1496, 0.0496, -0.0504],
[ 4.9156, 4.8156, 4.7156, ..., 0.2156, 0.1156, 0.0156]])
====End dists=====
====Start k =====
tensor([[8.5925e-01, 9.0338e-01, 9.4032e-01, ..., 1.8265e-04, 1.2002e-04,
7.8081e-05],
[8.0520e-01, 8.5569e-01, 9.0031e-01, ..., 2.8366e-04, 1.8841e-04,
1.2390e-04],
[7.4810e-01, 8.0329e-01, 8.5398e-01, ..., 4.2883e-04, 2.8780e-04,
1.9122e-04],
...,
[2.2622e-05, 3.5747e-05, 5.5924e-05, ..., 9.9721e-01, 9.8485e-01,
9.6297e-01],
[7.8152e-06, 1.2630e-05, 2.0206e-05, ..., 9.8887e-01, 9.9877e-01,
9.9873e-01],
[5.6628e-06, 9.2117e-06, 1.4836e-05, ..., 9.7702e-01, 9.9334e-01,
9.9988e-01]])
====End k=====
====Start attention_w =====
tensor([[1.2736e-01, 1.1960e-01, 1.1196e-01, ..., 1.3661e-05, 9.5400e-06,
6.6333e-06],
[1.1934e-01, 1.1328e-01, 1.0720e-01, ..., 2.1215e-05, 1.4976e-05,
1.0526e-05],
[1.1088e-01, 1.0635e-01, 1.0168e-01, ..., 3.2072e-05, 2.2876e-05,
1.6245e-05],
...,
[3.3530e-06, 4.7324e-06, 6.6587e-06, ..., 7.4582e-02, 7.8282e-02,
8.1809e-02],
[1.1584e-06, 1.6720e-06, 2.4059e-06, ..., 7.3958e-02, 7.9389e-02,
8.4847e-02],
[8.3933e-07, 1.2195e-06, 1.7664e-06, ..., 7.3072e-02, 7.8957e-02,
8.4945e-02]])
====End attention_w=====
====Start y_hat =====
tensor([2.6607, 2.6860, 2.7113, 2.7365, 2.7617, 2.7866, 2.8113, 2.8357, 2.8596,
2.8829, 2.9055, 2.9273, 2.9483, 2.9681, 2.9868, 3.0042, 3.0202, 3.0346,
3.0474, 3.0585, 3.0678, 3.0753, 3.0810, 3.0848, 3.0868, 3.0872, 3.0859,
3.0832, 3.0793, 3.0743, 3.0686, 3.0624, 3.0559, 3.0495, 3.0435, 3.0382,
3.0337, 3.0305, 3.0286, 3.0283, 3.0296, 3.0327, 3.0376, 3.0443, 3.0527,
3.0629, 3.0747, 3.0880, 3.1027, 3.1186])
====End y_hat=====Clearly, the narrower the kernel, the less smooth the estimate. At the same time, it adapts better to the local variations. Let’s look at the corresponding attention weights.
분명히 커널이 좁을수록 추정값이 덜 매끄러워집니다. 동시에 지역적 변화에 더 잘 적응합니다. 해당 어텐션 가중치를 살펴보겠습니다.
plot(x_train, y_train, x_val, y_val, kernels, names, attention=True)
위 코드는 이전에 정의한 plot 함수를 호출하여 다양한 가우시안 커널의 경우 Nadaraya-Watson 예측 결과를 시각화하는 과정입니다. attention=True로 설정함으로써 각 데이터 포인트의 주의 가중치(attention weights)를 시각화하는 작업을 수행합니다.
각 인자의 역할은 이전 설명과 동일합니다:
- x_train, y_train: 훈련 데이터의 입력과 출력 값
- x_val, y_val: 검증 데이터의 입력과 실제 출력 값
- kernels, names: 다양한 시그마 값에 대응하는 가우시안 커널 함수와 그에 대한 이름
- attention=True: 주의 가중치를 시각화할 것임을 나타내는 플래그
결과적으로, 이 코드는 각 시그마 값에 따라 다른 주의 가중치와 Nadaraya-Watson 예측 결과를 시각화하여 비교합니다.
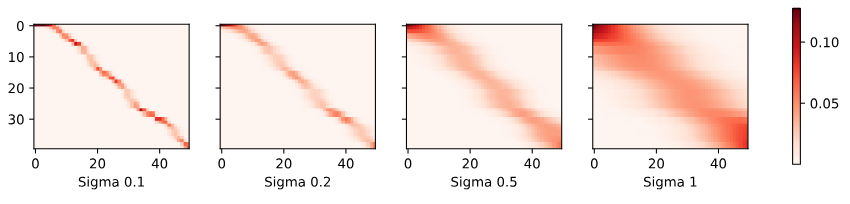
As we would expect, the narrower the kernel, the narrower the range of large attention weights. It is also clear that picking the same width might not be ideal. In fact, Silverman (1986) proposed a heuristic that depends on the local density. Many more such “tricks” have been proposed. It remains a valuable technique to date. For instance, Norelli et al. (2022) used a similar nearest-neighbor interpolation technique to design cross-modal image and text representations.
예상한 대로 커널이 좁을수록 큰 attention weights의 범위가 좁아집니다. 같은 너비를 선택하는 것이 이상적이지 않을 수도 있다는 것도 분명합니다. 실제로 Silverman(1986)은 지역 밀도(local density)에 의존하는 휴리스틱을 제안했습니다. 더 많은 그러한 "tricks"가 제안되었습니다. 그것은 현재까지 valuable 기술로 남아 있습니다. 예를 들어, Norelli 외. (2022)는 교차 모달 이미지(cross-modal image) 및 텍스트 표현(text representations)을 설계하기 위해 유사한 최근접 이웃 보간 기술(nearest-neighbor interpolation technique)을 사용했습니다.
The astute reader might wonder why this deep dive on a method that is over half a century old. First, it is one of the earliest precursors of modern attention mechanisms. Second, it is great for visualization. Third, and just as importantly, it demonstrates the limits of hand-crafted attention mechanisms. A much better strategy is to learn the mechanism, by learning the representations for queries and keys. This is what we will embark on in the following sections.
눈치 빠른 독자라면 반세기 이상 된 방법에 대해 왜 이렇게 깊이 파고드는지 의아해할 것입니다. 첫째, 그것은 현대 어텐션 메커니즘의 초기 선구자 중 하나입니다. 둘째, 시각화에 좋습니다. 셋째, 마찬가지로 중요한 것은 hand-crafted attention mechanisms의 한계를 보여줍니다. 훨씬 더 나은 전략은 쿼리 및 키에 대한 representations 을 학습하여 그 메커니즘을 배우는 것입니다. 이것이 우리가 다음 섹션에서 시작할 것입니다.
Nadaraya-Watson kernel regression이란?
Nadaraya-Watson kernel regression is a non-parametric regression technique used for estimating the conditional expectation of a dependent variable given an independent variable. It's a type of locally weighted regression that assigns different weights to each data point in the vicinity of the point where the prediction is being made. These weights are determined by a kernel function, typically a Gaussian or Epanechnikov kernel, which assigns higher weights to nearby points and lower weights to farther ones.
나다라야-와트슨 커널 회귀(Nadaraya-Watson kernel regression)는 독립 변수가 주어졌을 때 종속 변수의 조건부 기댓값을 추정하는 비모수 회귀 기법입니다. 이는 주변 데이터 포인트마다 다른 가중치를 할당하는 로컬 가중 회귀의 한 형태로, 예측이 이루어지는 지점 주변의 각 데이터 포인트에 가중치를 할당합니다. 이러한 가중치는 일반적으로 가우시안 또는 에파네치코프 커널과 같은 커널 함수에 의해 결정되며, 가까운 점에 높은 가중치를 부여하고 먼 점에는 낮은 가중치를 부여합니다.
Mathematically, given a set of input-output pairs (x_i, y_i), the Nadaraya-Watson estimator for predicting y at a new input x can be represented as:
수학적으로, 입력-출력 쌍 (x_i, y_i)의 집합이 주어진 경우 새로운 입력 x에서 y를 예측하기 위한 나다라야-와트슨 추정값은 다음과 같이 표현될 수 있습니다:
y_hat(x) = Σ (K(x - x_i) * y_i) / Σ K(x - x_i)
where K is the chosen kernel function. This method essentially emphasizes the influence of data points closer to the prediction point while downplaying the impact of distant points. It's particularly useful for handling non-linear relationships between variables and can adapt well to varying data densities in different regions.
여기서 K는 선택한 커널 함수를 나타냅니다. 이 방법은 실제로 예측 지점에 가까운 데이터 포인트의 영향을 강조하면서 먼 포인트의 영향을 감소시킵니다. 이는 변수 간의 비선형 관계를 처리하거나 서로 다른 데이터 밀도를 다양한 영역에서 잘 처리하는 데 특히 유용합니다.
Nadaraya-Watson kernel regression is commonly used for smoothing noisy data and capturing underlying trends or patterns in a flexible manner without making strong parametric assumptions about the relationship between variables.
나다라야-와트슨 커널 회귀는 노이즈가 있는 데이터를 스무딩하고 변수 간의 관계에 강력한 모수적 가정을 하지 않고 유연하게 잡아내는 데 일반적으로 사용되며, 변수 간의 관계를 다루는 데 유용한 방법입니다.
11.2.4. Summary
Nadaraya-Watson kernel regression is an early precursor of the current attention mechanisms. It can be used directly with little to no training or tuning, both for classification and regression. The attention weight is assigned according to the similarity (or distance) between query and key, and according to how many similar observations are available.
Nadaraya-Watson 커널 회귀는 현재 어텐션 메커니즘의 초기 선구자입니다. 분류 및 회귀 모두에 대해 훈련이나 튜닝이 거의 또는 전혀 없이 직접 사용할 수 있습니다. 어텐션 가중치는 쿼리와 키 사이의 유사성(또는 거리) 및 사용 가능한 유사한 관찰 수에 따라 할당됩니다.
Attention Pooling이란?
Attention pooling refers to a mechanism in machine learning and deep learning models where the model assigns varying degrees of importance or attention to different parts of the input data when making predictions. It's particularly common in sequence-to-sequence models, natural language processing tasks, and computer vision tasks.
어텐션 풀링(Attention Pooling)은 기계 학습과 딥 러닝 모델에서 입력 데이터의 다른 부분에 다양한 중요도나 주의를 할당하는 메커니즘을 의미합니다. 특히 시퀀스-투-시퀀스 모델, 자연어 처리 작업 및 컴퓨터 비전 작업에서 자주 사용됩니다.
In attention pooling, the model dynamically adjusts the weights or attention scores for each element of the input sequence based on its relevance to the current context. This allows the model to focus more on certain parts of the input when generating an output. For instance, in machine translation, the attention mechanism enables the model to align words in the source and target languages effectively, allowing it to generate accurate translations.
어텐션 풀링에서 모델은 현재 문맥과 관련성에 따라 입력 시퀀스의 각 요소에 가중치 또는 어텐션 점수를 동적으로 조정합니다. 이를 통해 모델은 출력을 생성할 때 입력의 특정 부분에 더 집중할 수 있습니다. 예를 들어 기계 번역에서 어텐션 메커니즘은 모델이 소스와 타겟 언어의 단어를 효과적으로 정렬하고 정확한 번역을 생성할 수 있게 합니다.
The attention pooling mechanism involves computing attention weights through various techniques like dot product attention, scaled dot product attention, and self-attention mechanisms (like those used in the Transformer model). These weights are then used to compute a weighted sum of the input elements, resulting in a context vector that is used for making predictions.
어텐션 풀링 메커니즘은 점곱 어텐션 dot product attention, 스케일링된 점곱 어텐션 scaled dot product attention, 그리고 트랜스포머 모델의 자기 어텐션 self-attention mechanisms 과 같은 다양한 기술을 사용하여 어텐션 가중치를 계산합니다. 이러한 가중치는 입력 요소의 가중합을 계산하는 데 사용되며, 이로써 예측을 위한 문맥 벡터를 생성합니다.
In summary, attention pooling is a crucial concept in deep learning models that enables them to focus on relevant parts of the input data while generating predictions, leading to improved performance in various sequence-related tasks.
요약하면, 어텐션 풀링은 딥 러닝 모델에서 예측을 생성하는 동안 입력 데이터의 관련 부분에 초점을 맞출 수 있도록 하는 중요한 개념으로, 다양한 시퀀스 관련 작업에서 성능을 향상시키는 데 기여하는 중요한 요소입니다.
11.2.5. Exercises

'Dive into Deep Learning > D2L Attention Mechanisms and Transformer' 카테고리의 다른 글
| D2L - 11.9. Large-Scale Pretraining with Transformers (0) | 2023.08.10 |
|---|---|
| D2L - 11.8. Transformers for Vision (0) | 2023.08.10 |
| D2L - 11.7. The Transformer Architecture (0) | 2023.08.09 |
| D2L - 11.6. Self-Attention and Positional Encoding (0) | 2023.08.09 |
| D2L - 11.5. Multi-Head Attention (0) | 2023.08.08 |
| D2L - 11.4. The Bahdanau Attention Mechanism (1) | 2023.08.08 |
| D2L - 11.3. Attention Scoring Functions (0) | 2023.08.07 |
| D2L - 11.1. Queries, Keys, and Values (0) | 2023.08.05 |
| D2L - 11. Attention Mechanisms and Transformers (0) | 2023.08.03 |

