11.6. Self-Attention and Positional Encoding — Dive into Deep Learning 1.0.0-beta0 documentation
d2l.ai
11.6. Self-Attention and Positional Encoding
In deep learning, we often use CNNs or RNNs to encode sequences. Now with attention mechanisms in mind, imagine feeding a sequence of tokens into an attention mechanism such that at each step, each token has its own query, keys, and values. Here, when computing the value of a token’s representation at the next layer, the token can attend (via its query vector) to each other token (matching based on their key vectors). Using the full set of query-key compatibility scores, we can compute, for each token, a representation by building the appropriate weighted sum over the other tokens. Because each token is attending to each other token (unlike the case where decoder steps attend to encoder steps), such architectures are typically described as self-attention models (Lin et al., 2017, Vaswani et al., 2017), and elsewhere described as intra-attention model (Cheng et al., 2016, Parikh et al., 2016, Paulus et al., 2017). In this section, we will discuss sequence encoding using self-attention, including using additional information for the sequence order.
딥 러닝에서 우리는 종종 CNN 또는 RNN을 사용하여 시퀀스를 인코딩합니다. 이제 어텐션 메커니즘을 염두에 두고 일련의 토큰을 어텐션 메커니즘에 공급하여 각 단계에서 각 토큰이 고유한 쿼리, 키 및 값을 갖도록 한다고 상상해 보십시오. 여기에서 다음 계층에서 토큰의 representation 값을 계산할 때 토큰은 쿼리 벡터를 통해 서로 토큰에 attend 할 수 있습니다(matching based on their key vectors). 쿼리 키 호환성 점수(compatibility scores)의 전체 집합을 사용하여 다른 토큰에 대해 적절한 weighted sum (가중 합계)를 구축하여 각 토큰에 대한 representation 을 계산할 수 있습니다. 각 토큰이 서로 토큰에 attending 하기 때문에(디코더 단계가 인코더 단계에 attend 하는 경우와 달리) 이러한 아키텍처는 일반적으로 self-attention 모델(Lin et al., 2017, Vaswani et al., 2017)로 설명됩니다. 인트라 어텐션 모델로 설명됩니다(Cheng et al., 2016, Parikh et al., 2016, Paulus et al., 2017). 이 섹션에서는 시퀀스 순서에 대한 추가 정보 사용을 포함하여 self-attention을 사용한 시퀀스 인코딩에 대해 설명합니다.
import math
import torch
from torch import nn
from d2l import torch as d2l
11.6.1. Self-Attention
Given a sequence of input tokens x1,…,xn where any xi∈ℝd (1≤i≤n), its self-attention outputs a sequence of the same length y1,…,yn, where like this according to the definition of attention pooling in (11.1.1).
임의의 xi∈ℝd(1≤i≤n)인 경우 입력 토큰 x1,...,xn의 시퀀스가 주어지면 self-attention은 동일한 길이 y1...,,yn의 시퀀스를 출력합니다. (11.1.1).

Using multi-head attention, the following code snippet computes the self-attention of a tensor with shape (batch size, number of time steps or sequence length in tokens, d). The output tensor has the same shape.
multi-head attention을 사용하여 다음 코드 스니펫은 shape (배치 크기, 시간 단계 수 또는 토큰의 시퀀스 길이, d)과 함께 텐서의 self-attention을 계산합니다. 출력 텐서는 동일한 모양을 갖습니다.
num_hiddens, num_heads = 100, 5
attention = d2l.MultiHeadAttention(num_hiddens, num_heads, 0.5)
batch_size, num_queries, valid_lens = 2, 4, torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens))
d2l.check_shape(attention(X, X, X, valid_lens),
(batch_size, num_queries, num_hiddens))위 코드는 멀티헤드 어텐션을 생성하고, 입력 데이터를 통해 멀티헤드 어텐션을 실행하며 출력의 형태를 확인하는 과정을 보여줍니다.
- num_hiddens, num_heads 변수를 설정하여 어텐션의 히든 크기와 헤드 개수를 정의합니다.
- d2l.MultiHeadAttention(num_hiddens, num_heads, 0.5) 코드를 통해 멀티헤드 어텐션 객체를 생성합니다. num_hiddens와 num_heads는 앞서 정의한 값이며, 0.5는 드롭아웃 비율을 나타냅니다.
- batch_size, num_queries, valid_lens 변수를 설정하여 미니배치 크기, 쿼리 개수, 그리고 유효한 쿼리 길이를 정의합니다.
- X = torch.ones((batch_size, num_queries, num_hiddens)) 코드를 통해 미니배치 크기와 쿼리 개수에 해당하는 크기의 3D 텐서 X를 생성합니다. 이 텐서는 쿼리 데이터를 나타냅니다.
- attention(X, X, X, valid_lens)를 호출하여 멀티헤드 어텐션을 실행합니다. 여기서 X를 쿼리, 키, 값으로 사용하며, valid_lens는 유효한 쿼리 길이를 나타냅니다.
- d2l.check_shape()를 사용하여 어텐션의 출력 형태를 확인합니다. 출력은 (batch_size, num_queries, num_hiddens)의 형태가 되어야 합니다. 이를 통해 코드의 정확성을 검증합니다.
이 코드는 멀티헤드 어텐션을 생성하고 실행하여 출력의 형태가 기대한 형태와 일치하는지 확인하는 예시입니다.

11.6.2. Comparing CNNs, RNNs, and Self-Attention
Let’s compare architectures for mapping a sequence of n tokens to another sequence of equal length, where each input or output token is represented by a d-dimensional vector. Specifically, we will consider CNNs, RNNs, and self-attention. We will compare their computational complexity, sequential operations, and maximum path lengths. Note that sequential operations prevent parallel computation, while a shorter path between any combination of sequence positions makes it easier to learn long-range dependencies within the sequence (Hochreiter et al., 2001).
n개 토큰의 시퀀스를 동일한 길이의 다른 시퀀스로 매핑하기 위한 아키텍처를 비교해 봅시다. 각 입력 또는 출력 토큰은 d차원 벡터로 표현됩니다. 구체적으로 CNN, RNN, self-attention을 고려할 것입니다. 계산 복잡성, 순차 작업 및 최대 경로 길이를 비교할 것입니다. 순차 작업(sequential operations)은 병렬 계산을 방지하는 반면 시퀀스 positions 조합 사이의 경로가 짧으면 시퀀스 내에서 장거리 종속성을 쉽게 학습할 수 있습니다(Hochreiter et al., 2001).

Consider a convolutional layer whose kernel size is k. We will provide more details about sequence processing using CNNs in later chapters. For now, we only need to know that since the sequence length is n, the numbers of input and output channels are both d, the computational complexity of the convolutional layer is 𝒪(knd2). As Fig. 11.6.1 shows, CNNs are hierarchical, so there are 𝒪(1) sequential operations and the maximum path length is 𝒪(n/k). For example, x1 and x5 are within the receptive field of a two-layer CNN with kernel size 3 in Fig. 11.6.1.
커널 크기가 k인 컨볼루션 계층을 고려하십시오. 이후 장에서 CNN을 사용한 시퀀스 처리에 대한 자세한 내용을 제공할 것입니다. 지금은 시퀀스 길이가 n이고 입력 및 출력 채널의 수가 모두 d이므로 컨볼루션 계층의 계산 복잡도는 𝒪(knd2)라는 것만 알면 됩니다. 그림 11.6.1에서 볼 수 있듯이 CNN은 계층적이므로 𝒪(1)개의 순차적 작업이 있고 최대 경로 길이는 𝒪(n/k)입니다. 예를 들어 x1과 x5는 그림 11.6.1에서 커널 크기가 3인 two-layer CNN의 receptive field 내에 있습니다.
When updating the hidden state of RNNs, multiplication of the d×d weight matrix and the d-dimensional hidden state has a computational complexity of 𝒪(d^2). Since the sequence length is n, the computational complexity of the recurrent layer is 𝒪(nd^2). According to Fig. 11.6.1, there are 𝒪(n) sequential operations that cannot be parallelized and the maximum path length is also 𝒪(n).
RNN의 hidden state를 업데이트할 때 d×d 가중치 행렬과 d차원 hidden state의 곱셈은 𝒪(d^2)의 계산 복잡도를 갖습니다. 시퀀스 길이가 n이므로 recurrent layer의 계산 복잡도는 𝒪(nd^2)입니다. 그림 11.6.1에 따르면 병렬화할 수 없는 순차 연산이 𝒪(n)개 있고 최대 경로 길이도 𝒪(n)입니다.
In self-attention, the queries, keys, and values are all n×d matrices. Consider the scaled dot-product attention in (11.3.6), where a n×d matrix is multiplied by a d×n matrix, then the output n×n matrix is multiplied by a n×d matrix. As a result, the self-attention has a 𝒪(n^2d) computational complexity. As we can see in Fig. 11.6.1, each token is directly connected to any other token via self-attention. Therefore, computation can be parallel with 𝒪(1) sequential operations and the maximum path length is also 𝒪(1).
self-attention에서 쿼리, 키, 값은 모두 n×d 행렬입니다. n×d 행렬에 d×n 행렬을 곱한 다음 출력 n×n 행렬에 n×d 행렬을 곱하는 (11.3.6)의 scaled dot-product attention를 고려하십시오. 결과적으로 self-attention은 𝒪(n^2d) 계산 복잡도를 가집니다. 그림 11.6.1에서 볼 수 있듯이 각 토큰은 self-attention을 통해 다른 토큰에 직접 연결됩니다. 따라서 연산은 𝒪(1) 순차 연산과 병행할 수 있으며 최대 경로 길이도 𝒪(1)입니다.
All in all, both CNNs and self-attention enjoy parallel computation and self-attention has the shortest maximum path length. However, the quadratic computational complexity with respect to the sequence length makes self-attention prohibitively slow for very long sequences.
대체로 CNN과 self-attention은 병렬 계산을 즐기고 self-attention은 최대 경로 길이(maximum path length)가 가장 짧습니다. 그러나 시퀀스 길이에 대한 2차 계산 복잡성(quadratic computational complexity)으로 인해 매우 긴 시퀀스의 경우 self-attention이 엄청나게 느려집니다.
quadratic computational complexity란?
'Quadratic computational complexity' refers to the growth rate of computational resources (such as time or memory) required by an algorithm as the input size increases. Specifically, it describes a scenario where the computational cost of an algorithm increases quadratically with the size of the input.
이차 계산 복잡도'는 알고리즘이 입력 크기가 증가함에 따라 필요한 계산 리소스(시간 또는 메모리와 같은)의 증가 속도를 나타냅니다. 구체적으로 말하면, 이는 알고리즘의 계산 비용이 입력 크기의 제곱에 비례하여 증가하는 상황을 의미합니다.
In mathematical terms, an algorithm is said to have quadratic complexity if the time or space it requires is proportional to the square of the input size. This is often denoted as O(n^2), where "n" represents the size of the input.
수학적으로, 알고리즘의 시간 또는 공간 요구 사항이 입력 크기의 제곱에 비례한다면 알고리즘은 이차 복잡도를 가진다고 말합니다. 이는 종종 O(n^2)로 표기되며, 여기서 "n"은 입력 크기를 나타냅니다.
Quadratic complexity is commonly associated with algorithms that involve nested loops, where each iteration of an outer loop contains one or more iterations of an inner loop. As the input size grows, the total number of iterations increases quadratically, leading to a significant increase in computational requirements.
이차 복잡도는 외부 루프의 각 반복이 내부 루프의 하나 이상의 반복을 포함하는 중첩 루프와 관련이 있습니다. 입력 크기가 증가함에 따라 전체 반복 횟수가 이차적으로 증가하므로 계산 요구 사항이 크게 증가합니다.
Algorithms with quadratic complexity are less efficient than those with linear (O(n)), logarithmic (O(log n)), or constant (O(1)) complexity. Therefore, in designing algorithms, it's generally preferable to minimize or avoid quadratic complexity whenever possible to ensure optimal performance as the input size grows.
이차 복잡도를 가진 알고리즘은 선형(O(n)), 로그(O(log n)), 또는 상수(O(1)) 복잡도를 가진 알고리즘보다 효율성이 낮습니다. 따라서 알고리즘을 설계할 때 입력 크기가 증가함에 따라 최적의 성능을 보장하기 위해 이차 복잡도를 최소화하거나 피하는 것이 일반적으로 바람직합니다.
11.6.3. Positional Encoding
Unlike RNNs, which recurrently process tokens of a sequence one by one, self-attention ditches sequential operations in favor of parallel computation. Note, however, that self-attention by itself does not preserve the order of the sequence. What do we do if it really matters that the model knows in which order the input sequence arrived?
시퀀스의 토큰을 하나씩 반복적으로 처리하는 RNN과 달리 self-attention은 병렬 계산을 위해 sequential operations을 버립니다. self-attention 자체는 시퀀스의 순서를 유지하지 않는 다는 것을 주목 하세요. 모델이 입력 시퀀스가 도착한 순서를 아는 것이 정말 중요하다면 어떻게 해야 할까요?
The dominant approach for preserving information about the order of tokens is to represent this to the model as an additional input associated with each token. These inputs are called positional encodings. and they can either be learned or fixed a priori. We now describe a simple scheme for fixed positional encodings based on sine and cosine functions (Vaswani et al., 2017).
토큰 순서에 대한 정보를 보존하기 위한 지배적인 접근 방식은 이를 각 토큰과 관련된 추가 입력으로 모델에 나타내는 것입니다. 이러한 입력을 positional encodings이라고 합니다. 그것들은 선험적으로 학습되거나 고정될 수 있습니다. 이제 사인 및 코사인 함수를 기반으로 fixed positional encodings을 위한 간단한 체계를 설명합니다(Vaswani et al., 2017).
Positional Encodings란?
'Positional Encodings'은 트랜스포머 모델과 같은 시퀀스-투-시퀀스 모델에서 단어의 상대적인 위치 정보를 모델에 전달하는 메커니즘입니다. 트랜스포머 모델은 셀프 어텐션을 통해 시퀀스 내의 단어들 간의 관계를 학습하지만, 이 모델은 단어의 위치 정보를 고려하지 않습니다. 따라서 같은 단어라고 하더라도 문장 내에서의 위치에 따라 의미가 달라질 수 있습니다.
이런 문제를 해결하기 위해 트랜스포머 모델은 'Positional Encodings'을 도입합니다. 이는 각 단어의 임베딩에 위치 정보를 더하는 방식으로 동작합니다. 이러한 위치 정보는 사인과 코사인 함수를 사용하여 계산되며, 이러한 함수의 주기와 진폭이 단어의 위치를 나타냅니다. 이렇게 함으로써 모델은 단어의 상대적인 위치 정보를 학습할 수 있게 됩니다.
예를 들어, "I love coding"이라는 문장에서 "love"라는 단어는 문장 맨 처음과는 다른 위치에 있을 때 다른 의미를 가지게 될 수 있습니다. 'Positional Encodings'을 사용하면 모델은 이러한 상대적인 위치 정보를 학습하여 단어의 의미를 더 정확하게 파악할 수 있습니다.
Suppose that the input representation X∈ℝn×d contains the d-dimensional embeddings for n tokens of a sequence. The positional encoding outputs X+P using a positional embedding matrix P∈ℝn×d of the same shape, whose element on the i th row and the (2j)th or the (2j+1)th column is
입력 representation X∈ℝn×d가 시퀀스의 n 토큰에 대한 d차원 임베딩을 포함한다고 가정합니다. positional encoding는 동일한 모양의 positional embedding matrix P∈ℝn×d를 사용하여 X+P를 출력하며, i번째 행과 (2j)번째 또는 (2j+1)번째 열의 요소는 다음과 같습니다.
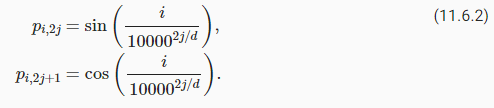
At first glance, this trigonometric-function design looks weird. Before explanations of this design, let’s first implement it in the following PositionalEncoding class.
언뜻 보면 이 삼각함수(trigonometric-function) 디자인이 이상해 보입니다. 이 디자인을 설명하기 전에 먼저 다음 PositionalEncoding 클래스에서 구현해 보겠습니다.
class PositionalEncoding(nn.Module): #@save
"""Positional encoding."""
def __init__(self, num_hiddens, dropout, max_len=1000):
super().__init__()
self.dropout = nn.Dropout(dropout)
# Create a long enough P
self.P = torch.zeros((1, max_len, num_hiddens))
X = torch.arange(max_len, dtype=torch.float32).reshape(
-1, 1) / torch.pow(10000, torch.arange(
0, num_hiddens, 2, dtype=torch.float32) / num_hiddens)
self.P[:, :, 0::2] = torch.sin(X)
self.P[:, :, 1::2] = torch.cos(X)
def forward(self, X):
X = X + self.P[:, :X.shape[1], :].to(X.device)
return self.dropout(X)위 코드는 트랜스포머 모델에서 사용되는 'Positional Encoding'을 구현한 클래스입니다. 트랜스포머 모델은 단어의 순서 정보를 어텐션 메커니즘을 사용하여 처리하므로, 단어의 상대적인 위치 정보를 인코딩해야 합니다. 이를 위해 'Positional Encoding'이 사용됩니다.
클래스의 구성요소를 하나씩 설명해보겠습니다.
- __init__(self, num_hiddens, dropout, max_len=1000):
- num_hiddens: 임베딩된 토큰의 차원을 나타내는 매개변수입니다.
- dropout: 드롭아웃 확률을 나타내는 매개변수입니다.
- max_len: 시퀀스의 최대 길이를 나타내는 매개변수로, 기본값은 1000입니다.
- self.dropout: 드롭아웃 레이어를 초기화합니다.
- self.P: 시퀀스의 각 위치에 대한 positional encoding을 저장하는 텐서입니다.
- X는 트랜스포머에서 사용되는 각 위치의 positional encoding을 생성하는 역할을 합니다. 이때 max_len만큼의 숫자 시퀀스를 생성하고, 이를 이용하여 각 위치의 positional encoding 값을 계산합니다.
torch.pow(10000, ...)를 통해 positional encoding 값의 변화율을 결정합니다.
self.P의 홀수 인덱스 위치에는 사인 값을, 짝수 인덱스 위치에는 코사인 값을 저장하여 positional encoding 값을 구성합니다.
- forward(self, X):
- X: 임베딩된 입력 토큰 텐서입니다.
- forward 메서드는 입력으로 받은 임베딩된 토큰 X에 positional encoding을 더하는 과정을 수행합니다.
- X에 self.P를 더하여 positional encoding을 적용합니다. 이 때 입력의 길이에 맞추어 self.P의 길이를 잘라내어 적용합니다. (self.P는 토큰의 개수에 맞게 잘라서 가져온 후, X와 더하여 위치 정보를 추가합니다.)
- 이후 self.dropout을 적용하여 드롭아웃을 적용한 결과를 반환합니다.
위 클래스는 트랜스포머 모델에서 입력 임베딩에 positional encoding을 추가하는 역할을 수행합니다. 이를 통해 모델은 단어의 상대적인 위치 정보를 반영하여 문장 내 단어의 순서를 고려할 수 있게 됩니다.
In the positional embedding matrix P, rows correspond to positions within a sequence and columns represent different positional encoding dimensions. In the example below, we can see that the 6th and the 7th columns of the positional embedding matrix have a higher frequency than the 8th and the 9th columns. The offset between the 6th and the 7th (same for the 8th and the 9th) columns is due to the alternation of sine and cosine functions.
positional embedding matrix P에서 행rows 은 시퀀스 내의 위치positions 에 해당하고 열columns 은 서로 다른 positional encoding dimensions을 나타냅니다. 아래 예에서 positional embedding matrix 의 6번째 및 7번째 열이 8번째 및 9번째 열보다 높은 빈도를 갖는 것을 볼 수 있습니다. 6번째 열과 7번째 열(8번째 및 9번째 열과 동일) 사이의 오프셋은 사인 및 코사인 함수의 교체 alternation로 인한 것입니다.
encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
X = pos_encoding(torch.zeros((1, num_steps, encoding_dim)))
P = pos_encoding.P[:, :X.shape[1], :]
d2l.plot(torch.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',
figsize=(6, 2.5), legend=["Col %d" % d for d in torch.arange(6, 10)])- encoding_dim은 positional encoding 차원의 크기를, num_steps는 시퀀스의 길이를 나타냅니다.
- PositionalEncoding 클래스를 이용해 pos_encoding 객체를 생성합니다. 이 객체는 위치 정보를 포함한 positional encoding을 생성하는 역할을 합니다.
- torch.zeros((1, num_steps, encoding_dim))를 통해 임의의 입력 데이터를 생성하고, 이를 pos_encoding에 적용하여 positional encoding을 얻습니다.
- pos_encoding.P[:, :X.shape[1], :]를 통해 얻은 positional encoding 텐서를 P에 저장합니다. 이때 텐서의 형태는 (1, num_steps, encoding_dim)입니다.
- d2l.plot 함수를 이용해 특정 인덱스 범위의 positional encoding을 시각화합니다. torch.arange(6, 10)은 6부터 9까지의 열을 선택하여 시각화하겠다는 의미입니다.
- xlabel='Row (position)'를 통해 x 축의 레이블을 설정하고, figsize=(6, 2.5)로 그림의 크기를 지정합니다.
- legend=["Col %d" % d for d in torch.arange(6, 10)]를 통해 범례에 각 열의 레이블을 추가합니다.
이 코드는 PositionalEncoding을 통해 생성한 positional encoding을 시각화하여, 각 위치와 각 차원의 변화를 확인하는 역할을 합니다.


11.6.3.1. Absolute Positional Information
To see how the monotonically decreased frequency along the encoding dimension relates to absolute positional information, let’s print out the binary representations of 0,1,…,7. As we can see, the lowest bit, the second-lowest bit, and the third-lowest bit alternate on every number, every two numbers, and every four numbers, respectively.
인코딩 차원을 따라 단조롭게 감소된 frequency 가 절대 위치 정보와 어떻게 관련되는지 확인하기 위해 0,1,…,7의 이진 표현을 출력해 보겠습니다. 보시다시피 가장 낮은 비트, 두 번째로 낮은 비트 및 세 번째로 낮은 비트는 각각 모든 숫자, 두 개의 숫자 및 네 개의 숫자마다 번갈아 나타납니다.
for i in range(8):
print(f'{i} in binary is {i:>03b}')이 코드는 0부터 7까지의 정수를 이진수로 나타내는 예시를 보여주는 반복문입니다.
- for i in range(8):는 0부터 7까지의 정수를 반복하는 루프입니다.
- f'{i} in binary is {i:>03b}'은 문자열 포맷팅을 사용하여 출력될 문자열을 생성합니다. 여기서 i는 현재 정수 값이며, i:>03b는 해당 값을 이진수로 나타내는 형식입니다. >03은 문자열을 오른쪽 정렬하고, 최소 3자리로 표현하도록 지시하는 것을 의미합니다.
결과적으로 이 코드는 0부터 7까지의 정수를 이진수로 변환하여 출력합니다. 출력 형태는 각 정수와 해당 이진수 표현을 보여주며, 이때 이진수는 최소 3자리로 오른쪽 정렬된 형태로 출력됩니다.
0 in binary is 000
1 in binary is 001
2 in binary is 010
3 in binary is 011
4 in binary is 100
5 in binary is 101
6 in binary is 110
7 in binary is 111
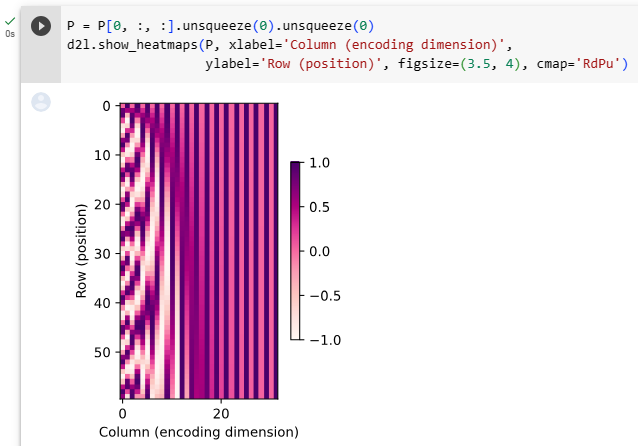
In binary representations, a higher bit has a lower frequency than a lower bit. Similarly, as demonstrated in the heat map below, the positional encoding decreases frequencies along the encoding dimension by using trigonometric functions. Since the outputs are float numbers, such continuous representations are more space-efficient than binary representations.
binary representations에서 높은 비트는 낮은 비트보다 주파수가 낮습니다. 유사하게, 아래의 열지도heat map에서 볼 수 있듯이 positional encoding은 삼각 함수를 사용하여 encoding dimension을 따라 frequencies 를 줄입니다. 출력은 부동 소수점 숫자이므로 이러한 연속 representations 은 이진 표현보다 공간 효율적입니다.
P = P[0, :, :].unsqueeze(0).unsqueeze(0)
d2l.show_heatmaps(P, xlabel='Column (encoding dimension)',
ylabel='Row (position)', figsize=(3.5, 4), cmap='Blues')이 코드는 위치 인코딩 행렬 P를 시각화하여 행과 열에 대한 히트맵을 표시하는 부분입니다.
- P = P[0, :, :].unsqueeze(0).unsqueeze(0)는 P 행렬을 시각화할 수 있도록 데이터 형태를 조정합니다. P는 (1, max_len, num_hiddens)의 형태를 가지는데, 이를 (1, num_steps, encoding_dim)의 형태로 변환합니다. 이는 히트맵을 표시하기 위해 데이터 형태를 변경하는 단계입니다.
- d2l.show_heatmaps(P, xlabel='Column (encoding dimension)', ylabel='Row (position)', figsize=(3.5, 4), cmap='Blues')는 d2l 라이브러리의 show_heatmaps 함수를 사용하여 히트맵을 시각화합니다. 여기서 P를 시각화하며, x축은 인코딩 차원(column)을 나타내고, y축은 위치(row)를 나타냅니다. figsize는 그림 크기를 지정하고, cmap은 색상 맵을 지정합니다.
이 코드는 위치 인코딩 행렬을 히트맵으로 시각화하여, 행과 열에 따른 패턴을 확인할 수 있도록 합니다.


11.6.3.2. Relative Positional Information
Besides capturing absolute positional information, the above positional encoding also allows a model to easily learn to attend by relative positions. This is because for any fixed position offset δ (delta), the positional encoding at position i+δ can be represented by a linear projection of that at position i.
absolute positional information를 캡처하는 것 외에도 위의 positional encoding을 사용하면 모델이 relative positions에 attend 하는 방법을 쉽게 배울 수 있습니다. 이는 임의의 고정된 위치 오프셋 δ(델타)에 대해 위치 i+δ에서의 위치 인코딩이 위치 i에서의 선형 프로젝션으로 표현될 수 있기 때문입니다.

이 projection은 수학적으로 설명 될 수 있습니다.

where the 2×2 projection matrix does not depend on any position index i.
여기서 2×2 프로젝션 매트릭스는 위치 인덱스 i에 의존하지 않습니다.
11.6.4. Summary
In self-attention, the queries, keys, and values all come from the same place. Both CNNs and self-attention enjoy parallel computation and self-attention has the shortest maximum path length. However, the quadratic computational complexity with respect to the sequence length makes self-attention prohibitively slow for very long sequences. To use the sequence order information, we can inject absolute or relative positional information by adding positional encoding to the input representations.
self-attention에서 쿼리, 키 및 값은 모두 같은 위치에서 옵니다. CNN과 self-attention 모두 병렬 계산을 즐기고 self-attention은 최대 경로 길이가 가장 짧습니다. 그러나 시퀀스 길이에 대한 2차(quadratic ) 계산 복잡성으로 인해 매우 긴 시퀀스의 경우 self-attention이 엄청나게 느려집니다. 시퀀스 순서 정보를 사용하기 위해 입력 표현에 위치 인코딩을 추가하여 절대 또는 상대 위치 정보를 주입할 수 있습니다.
11.6.5. Exercises
- Suppose that we design a deep architecture to represent a sequence by stacking self-attention layers with positional encoding. What could be issues?
- Can you design a learnable positional encoding method?
- Can we assign different learned embeddings according to different offsets between queries and keys that are compared in self-attention? Hint: you may refer to relative position embeddings (Huang et al., 2018, Shaw et al., 2018).
Self-Attention이란?
'Self-attention'은 주어진 입력 시퀀스 내의 요소들 간의 상관 관계를 계산하기 위해 사용되는 메커니즘입니다. 주로 자연어 처리와 기계 번역과 같은 sequence-to-sequence 모델에서 사용되며, 특히 트랜스포머 (Transformer)와 같은 모델에서 널리 사용됩니다.
Self-attention은 입력 시퀀스의 각 요소가 다른 모든 요소와 얼마나 관련 있는지를 계산하며, 이를 통해 문장 내에서 단어들 간의 의미적 연관성을 포착할 수 있습니다. 이는 문맥을 파악하거나 문장 내에서 중요한 단어를 감지하는 데 유용합니다.
Self-attention 메커니즘은 다양한 방식으로 구현될 수 있지만, 대표적으로 'Scaled Dot-Product Attention', 'Additive Attention', 'Multi-Head Attention' 등이 있습니다. 이러한 메커니즘을 통해 모델은 입력 시퀀스의 각 요소에 대해 가중치를 할당하여 문맥을 이해하고, 이를 기반으로 다음 출력을 생성하거나 문장을 번역하는 작업을 수행할 수 있습니다.
'Dive into Deep Learning > D2L Attention Mechanisms and Transformer' 카테고리의 다른 글
| D2L - 11.9. Large-Scale Pretraining with Transformers (0) | 2023.08.10 |
|---|---|
| D2L - 11.8. Transformers for Vision (0) | 2023.08.10 |
| D2L - 11.7. The Transformer Architecture (0) | 2023.08.09 |
| D2L - 11.5. Multi-Head Attention (0) | 2023.08.08 |
| D2L - 11.4. The Bahdanau Attention Mechanism (1) | 2023.08.08 |
| D2L - 11.3. Attention Scoring Functions (0) | 2023.08.07 |
| D2L - 11.2. Attention Pooling by Similarity (0) | 2023.08.06 |
| D2L - 11.1. Queries, Keys, and Values (0) | 2023.08.05 |
| D2L - 11. Attention Mechanisms and Transformers (0) | 2023.08.03 |

