https://d2l.ai/chapter_attention-mechanisms-and-transformers/attention-scoring-functions.html
11.3. Attention Scoring Functions — Dive into Deep Learning 1.0.0-beta0 documentation
d2l.ai
11.3. Attention Scoring Functions
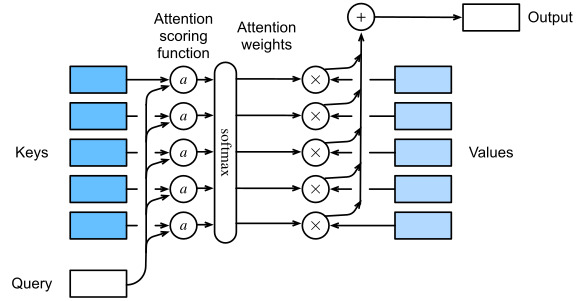
In Section 11.2, we used a number of different distance-based kernels, including a Gaussian kernel to model interactions between queries and keys. As it turns out, distance functions are slightly more expensive to compute than inner products. As such, with the softmax operation to ensure nonnegative attention weights, much of the work has gone into attention scoring functions α in (11.1.3) and Fig. 11.3.1 that are simpler to compute.
섹션 11.2에서 쿼리와 키 간의 상호 작용을 모델링하기 위해 가우시안 커널을 포함하여 다양한 거리 기반 커널을 사용했습니다. 결과적으로 거리 함수는 내적(inner products)보다 계산 비용이 약간 더 비쌉니다. 이와 같이 음이 아닌 attention weights를 보장하기 위한 softmax operation으로 많은 작업이 (11.1.3) 및 그림 11.3.1의 attention scoring functions α로 진행되었으며 이는 계산하기 더 간단합니다.
Innder products (내적) 이란?
"Inner products" refer to a mathematical operation that takes two vectors and produces a scalar value. Also known as a dot product, it quantifies the similarity or alignment between two vectors by calculating the sum of the products of their corresponding components.
"내적"은 두 개의 벡터를 가져와서 스칼라 값을 생성하는 수학적 연산을 나타냅니다. 내적은 또한 점곱이라고도 하며, 두 벡터 간의 대응하는 구성 요소의 곱의 합을 계산하여 두 벡터의 유사성이나 정렬을 측정합니다.
For two vectors x and y in an n-dimensional space, the inner product is calculated as:
n-차원 공간에서 두 벡터 x와 y에 대해서 내적은 다음과 같이 계산됩니다:
x ⋅ y = x₁ * y₁ + x₂ * y₂ + ... + xₙ * yₙ
This operation is often used in various mathematical and computational contexts, such as vector spaces, linear algebra, functional analysis, and machine learning algorithms. Inner products have a wide range of applications, including measuring angles between vectors, calculating distances, finding projections, and solving optimization problems.
이 연산은 벡터 공간, 선형 대수학, 함수 해석 및 기계 학습 알고리즘과 같은 다양한 수학적 및 계산적 맥락에서 사용됩니다. 내적은 벡터 간의 각도를 측정하거나 거리를 계산하며, 투영을 찾는 데 사용되며, 최적화 문제를 해결하는 등 다양한 응용 분야가 있습니다.
import math
import torch
from torch import nn
from d2l import torch as d2l
11.3.1. Dot Product Attention
Let’s review the attention function (without exponentiation) from the Gaussian kernel for a moment:
잠시 동안 Gaussian kernel 의 attention function(지수 없음)를 검토해 보겠습니다.
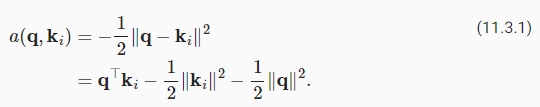
First, note that the last term depends on q only. As such it is identical for all (q,ki) pairs. Normalizing the attention weights to 1, as is done in (11.1.3), ensures that this term disappears entirely. Second, note that both batch and layer normalization (to be discussed later) lead to activations that have well-bounded, and often constant norms ‖ki‖≈const. This is the case, for instance, whenever the keys ki were generated by a layer norm. As such, we can drop it from the definition of α without any major change in the outcome.
첫째, last term는 q에만 의존한다는 점에 유의하십시오. 따라서 모든 (q,ki) 쌍에 대해 동일합니다. (11.1.3)에서와 같이 attention weights를 1로 정규화하면 이 term 가 완전히 사라집니다. 둘째, batch 및 layer normalization(나중에 논의됨) 모두 well-bounded하고 종종 constant norms인 ki‖≈const를 갖는 활성화로 이어집니다. 예를 들어 키 ki가 layer norm에 의해 생성될 때마다 그렇습니다. 따라서 결과에 큰 변화 없이 α의 정의에서 제외할 수 있습니다.
Last, we need to keep the order of magnitude of the arguments in the exponential function under control. Assume that all the elements of the query q∈ℝ^d and the key ki∈ℝ^d are independent and identically drawn random variables with zero mean and unit variance. The dot product between both vectors has zero mean and a variance of d. To ensure that the variance of the dot product still remains one regardless of vector length, we use the scaled dot-product attention scoring function. That is, we rescale the dot-product by 1/ √d. We thus arrive at the first commonly used attention function that is used, e.g., in Transformers (Vaswani et al., 2017):
마지막으로 지수 함수(exponential function)에서 인수의 크기(magnitude ) 순서를 제어할 필요가 있습니다. 쿼리 q∈ℝ^d 및 키 ki∈ℝ^d의 모든 요소가 평균이 0이고 단위 분산이 있는 독립적이고 동일하게 그려진 확률 변수라고 가정합니다. 두 벡터 간의 내적(dot product)은 zero mean이고 a variance of d입니다. 벡터 길이에 관계없이 내적(dot product)의 분산(variance )이 여전히 1로 유지되도록 scaled dot-product attention scoring function를 사용합니다. 즉, 내적(dot-product)을 1/ √d로 재조정합니다. 따라서 우리는 예를 들어 Transformers(Vaswani et al., 2017)에서 사용되는 첫 번째 일반적으로 사용되는 attention function에 도달합니다.

Scaled dot product attention이란?
'Scaled Dot Product Attention'은 트랜스포머(Transformer)와 같은 인공 신경망 모델에서 사용되는 어텐션(Attention) 메커니즘 중 하나입니다. 이 어텐션 메커니즘은 특정 쿼리(Query)와 키(Key) 사이의 관계를 계산하여 가중치를 생성하고, 이를 값(Value)에 적용하여 가중 평균을 계산하는 방법을 확장한 것입니다.
'Scaled Dot Product Attention'에서 "Scaled"는 어텐션 스코어를 정규화하기 위해 사용되는 조정 상수(scale factor)입니다. 어텐션 스코어는 쿼리와 각 키 사이의 내적(Dot Product)을 의미합니다. 내적을 스케일링하면 어텐션 스코어의 크기가 키의 차원 수에 영향을 받지 않게 됩니다.
이러한 접근 방식은 어텐션 스코어의 분포를 조절하여 학습을 안정화하고, 어텐션 가중치를 좀 더 관리 가능한 범위로 조절하여 기울기 소실과 폭주 문제를 완화하는 데 도움을 줍니다. 이러한 메커니즘은 트랜스포머의 인코더-디코더 어텐션, 멀티헤드 어텐션 등 다양한 컨텍스트에서 사용되며, 특히 자연어 처리 및 기계 번역과 같은 태스크에서 중요한 역할을 합니다.
Note that attention weights α still need normalizing. We can simplify this further via (11.1.3) by using the softmax operation:
attention 가중치 α는 여전히 정규화가 필요합니다. softmax 작업을 사용하여 (11.1.3)을 통해 이를 더 단순화할 수 있습니다.


As it turns out, all popular attention mechanisms use the softmax, hence we will limit ourselves to that in the remainder of this chapter.
밝혀진 바와 같이 모든 인기 있는 어텐션 메커니즘은 소프트맥스를 사용하므로 이 장의 나머지 부분에서는 이에 대해 제한할 것입니다.
11.3.2. Convenience Functions
We need a few functions to make the attention mechanism efficient to deploy. This includes tools to deal with strings of variable lengths (common for natural language processing) and tools for efficient evaluation on minibatches (batch matrix multiplication).
attention mechanism을 효율적으로 배포하려면 몇 가지 기능이 필요합니다. 여기에는 variable lengths의 문자열을 처리하는 도구(자연어 처리에 일반적임)와 미니배치(배치 행렬 곱셈)에서 efficient evaluation를 위한 도구가 포함됩니다.
11.3.2.1. Masked Softmax Operation
One of the most popular applications of the attention mechanism is to sequence models. Hence we need to be able to deal with sequences of different lengths. In some cases, such sequences may end up in the same minibatch, necessitating padding with dummy tokens for shorter sequences (see Section 10.5 for an example). These special tokens do not carry meaning. For instance, assume that we have the following three sentences:
attention mechanism의 가장 인기 있는 애플리케이션 중 하나는 sequence models입니다. 따라서 길이가 다른 시퀀스를 처리할 수 있어야 합니다. 경우에 따라 이러한 시퀀스는 더 짧은 시퀀스를 위해 dummy tokens으로 padding해야 하는 동일한 미니 배치로 끝날 수 있습니다(예는 섹션 10.5 참조). 이러한 특수 토큰에는 의미가 없습니다. 예를 들어, 다음 세 문장이 있다고 가정합니다.
(길이를 같게 하기 위해 넣은 blank는 아무런 의미가 없다.)
Dive into Deep Learning
Learn to code <blank>
Hello world <blank> <blank>
Since we do not want blanks in our attention model we simply need to limit ∑n i=1 α(q,ki)vi to ∑l i=1 α(q,ki)vi for however long l ≤ n the actual sentence is. Since it is such a common problem, it has a name: the masked softmax operation.
우리는 attention model에서 공백을 원하지 않기 때문에 실제 문장이 l ≤ n인 경우 ∑n i=1 α(q,ki)vi를 ∑l i=1 α(q,ki)vi로 제한하기만 하면 됩니다. 이는 매우 일반적인 문제이므로 masked softmax operation이라는 이름이 있습니다.
Let’s implement it. Actually, the implementation cheats ever so slightly by setting the values to zero vi=0 for i>l. Moreover, it sets the attention weights to a large negative number, such as −106 in order to make their contribution to gradients and values vanish in practice. This is done since linear algebra kernels and operators are heavily optimized for GPUs and it is faster to be slightly wasteful in computation rather than to have code with conditional (if then else) statements.
이제 이것을 구현합시다. 실제로 구현은 i>l에 대해 vi=0으로 값을 0으로 설정하여 약간 속입니다. 또한 attention weights를 -10**6과 같은 큰 음수로 설정하여 기울기와 값에 대한 기여도가 실제로 사라지도록 합니다. 이것은 선형 대수학 커널과 연산자가 GPU에 크게 최적화되어 있고 조건문(if then else)이 있는 코드를 사용하는 것보다 계산에서 약간 낭비하는 것이 더 빠르기 때문에 수행됩니다.
(blank가 있는 부분은 값을 0으로 설정하고 attention weights를 큰 음수로 설정해 기울기가 사라지도록 해서 계산에서 제외 시킵니다.)
def masked_softmax(X, valid_lens): #@save
"""Perform softmax operation by masking elements on the last axis."""
# X: 3D tensor, valid_lens: 1D or 2D tensor
def _sequence_mask(X, valid_len, value=0):
maxlen = X.size(1)
mask = torch.arange((maxlen), dtype=torch.float32,
device=X.device)[None, :] < valid_len[:, None]
X[~mask] = value
return X
if valid_lens is None:
return nn.functional.softmax(X, dim=-1)
else:
shape = X.shape
if valid_lens.dim() == 1:
valid_lens = torch.repeat_interleave(valid_lens, shape[1])
else:
valid_lens = valid_lens.reshape(-1)
# On the last axis, replace masked elements with a very large negative
# value, whose exponentiation outputs 0
X = _sequence_mask(X.reshape(-1, shape[-1]), valid_lens, value=-1e6)
return nn.functional.softmax(X.reshape(shape), dim=-1)
이 코드는 마스크된 소프트맥스 연산을 수행하는 함수인 masked_softmax를 정의합니다.
- _sequence_mask 함수 정의: 이 함수는 시퀀스 길이에 따라 마스크를 생성하는 기능을 합니다. 주어진 시퀀스 길이(valid_len)보다 긴 부분을 마스크로 처리하여 지정된 값(기본값은 0)으로 설정합니다.
- masked_softmax 함수 정의: 이 함수는 입력 텐서 X와 유효한 길이 정보 valid_lens를 받아 마스크된 소프트맥스 연산을 수행합니다.
- valid_lens가 주어지지 않은 경우에는 nn.functional.softmax를 사용하여 전체 소프트맥스를 계산합니다.
- valid_lens가 주어진 경우에는 입력 텐서의 shape를 확인하고, 만약 valid_lens가 1차원 텐서인 경우 각 위치에 대해 동일한 값을 반복합니다. 그렇지 않은 경우, valid_lens를 1차원으로 변형합니다.
- 마지막 축에서 마스크된 원소를 매우 작은 음수 값(-1e6)으로 대체하여 소프트맥스의 분모로 들어가지 않도록 합니다.
- 최종적으로 소프트맥스를 계산하고, 마스크가 적용된 부분의 출력이 0이 되도록 처리합니다.
이 함수는 특히 시계열 데이터와 같은 길이가 다양한 시퀀스에 대한 소프트맥스 연산을 처리하는 데 유용하며, 모델이 패딩된 부분을 무시하고 중요한 정보만 고려할 수 있게 합니다.
To illustrate how this function works, consider a minibatch of two examples of size 2×4, where their valid lengths are 2 and 3, respectively. As a result of the masked softmax operation, values beyond the valid lengths for each pair of vectors are all masked as zero.
이 함수가 어떻게 작동하는지 설명하기 위해 유효한 길이가 각각 2와 3인 크기 2×4의 두 가지 예의 미니 배치를 고려하십시오. 마스킹된 소프트맥스 연산의 결과 각 벡터 쌍의 유효 길이를 초과하는 값은 모두 0으로 마스킹됩니다.
masked_softmax(torch.rand(2, 2, 4), torch.tensor([2, 3]))위의 코드는 masked_softmax 함수를 사용하여 소프트맥스 연산을 수행하는 예시입니다.
- torch.rand(2, 2, 4): 크기가 (2, 2, 4)인 무작위 값을 가진 3D 텐서입니다.
- torch.tensor([2, 3]): 길이가 2인 1D 텐서로, 각 원소는 시퀀스 길이를 나타냅니다.
masked_softmax 함수는 입력 텐서와 유효한 길이 정보를 받아 소프트맥스 연산을 수행합니다. 이 예시에서는 다음과 같이 동작합니다:
- 입력 텐서의 크기: (2, 2, 4)
- 유효한 길이 정보: [2, 3]
입력 텐서의 각 요소에 대해 소프트맥스를 계산하되, 유효한 길이에 따라 패딩된 부분은 처리하지 않고 아주 작은 음수 값(-1e6)으로 대체하여 해당 부분의 소프트맥스 값이 0이 되도록 합니다. 결과적으로, 소프트맥스 연산을 수행한 결과가 반환됩니다.

예

If we need more fine-grained control to specify the valid length for each of the two vectors per example, we simply use a two-dimensional tensor of valid lengths. This yields:
예제당 두 벡터 각각에 대해 유효한 길이를 지정하기 위해 더 세밀한 제어가 필요한 경우 유효한 길이의 2차원 텐서를 사용하기만 하면 됩니다. 결과는 다음과 같습니다.
masked_softmax(torch.rand(2, 2, 4), torch.tensor([[1, 3], [2, 4]]))위의 코드는 masked_softmax 함수를 사용하여 소프트맥스 연산을 수행하는 또 다른 예시입니다.
- torch.rand(2, 2, 4): 크기가 (2, 2, 4)인 무작위 값을 가진 3D 텐서입니다.
- torch.tensor([[1, 3], [2, 4]]): 크기가 (2, 2)인 2D 텐서로, 각 행별로 시퀀스 길이를 나타냅니다.
이 경우, masked_softmax 함수가 다음과 같이 동작합니다:
- 입력 텐서의 크기: (2, 2, 4)
- 유효한 길이 정보: [[1, 3], [2, 4]]
입력 텐서의 각 요소에 대해 소프트맥스를 계산하되, 각 행별로 다른 길이를 가지므로 각 행의 마지막 원소를 제외한 부분은 아주 작은 음수 값(-1e6)으로 대체하여 해당 부분의 소프트맥스 값이 0이 되도록 합니다. 결과적으로, 소프트맥스 연산을 수행한 결과가 반환됩니다.

11.3.2.2. Batch Matrix Multiplication
Another commonly used operation is to multiply batches of matrices with another. This comes in handy when we have minibatches of queries, keys, and values. More specifically, assume that
일반적으로 사용되는 또 다른 작업은 행렬 배치를 다른 행렬과 곱하는 것입니다. 이는 쿼리, 키 및 값의 미니 배치가 있을 때 유용합니다. 더 구체적으로 가정하자면

Then the batch matrix multiplication (BMM) computes the element-wise product
그런 다음 BMM(배치 행렬 곱셈)은 요소별 곱을 계산합니다.

Let’s see this in action in a deep learning framework.
딥 러닝 프레임워크에서 이것이 어떻게 작동하는지 살펴보겠습니다.
Q = torch.ones((2, 3, 4))
K = torch.ones((2, 4, 6))
d2l.check_shape(torch.bmm(Q, K), (2, 3, 6))위의 코드는 행렬 곱셈을 사용하여 어텐션을 계산하는 예시입니다.
- Q: 크기가 (2, 3, 4)인 텐서입니다.
- K: 크기가 (2, 4, 6)인 텐서입니다.
여기서 torch.bmm(Q, K)는 두 배치 행렬 텐서 Q와 K 간의 배치 매트릭스 곱셈을 수행하는 연산입니다. 이 결과 텐서의 크기는 (2, 3, 6)이 됩니다.
따라서 위의 코드에서 d2l.check_shape(torch.bmm(Q, K), (2, 3, 6))는 행렬 곱셈의 결과가 기대한 크기인 (2, 3, 6)과 동일한지를 확인하는 코드입니다. 만약 결과 텐서의 크기가 기대한 크기와 다르다면 오류가 발생할 것입니다.

batch matrix multiplation이란?
배치 행렬 곱셈(batch matrix multiplication)은 딥러닝에서 자주 사용되는 연산 중 하나로, 배치 처리를 통해 여러 입력 데이터에 대한 행렬 곱셈을 동시에 수행하는 것을 의미합니다. 이 연산은 주로 어텐션 메커니즘, 순환 신경망 (RNN), 변환자 (Transformer) 등에서 활발하게 활용됩니다.
배치 행렬 곱셈은 다음과 같이 정의됩니다:
- 두 개의 입력 텐서 X와 Y가 주어집니다.
- X의 마지막 차원의 크기와 Y의 뒤에서 두 번째 차원의 크기가 일치해야 합니다. 즉, X의 크기는 (batch_size, d1, d2)이고 Y의 크기는 (batch_size, d2, d3)이라면 d2는 동일한 값이어야 합니다.
- 결과 텐서 Z의 크기는 (batch_size, d1, d3)가 됩니다.
이러한 배치 행렬 곱셈을 수행하면 각 배치의 입력 행렬이 행렬 곱셈을 거쳐 결과 행렬로 변환됩니다. 이 과정은 각각의 배치 데이터에 대해 병렬적으로 이루어지며, 배치 처리를 통해 연산 속도를 향상시킬 수 있습니다.
배치 행렬 곱셈은 신경망의 다양한 부분에서 사용되며, 주로 선형 변환과 어텐션 계산에 활용됩니다.

11.3.3. Scaled Dot-Product Attention
Let’s return to the dot-product attention introduced in (11.3.2). In general, it requires that both the query and the key have the same vector length, say d, even though this can be addressed easily by replacing q⊤k with q⊤Mk where M is a suitably chosen matrix to translate between both spaces. For now assume that the dimensions match.
(11.3.2)에서 소개한 내적 주의로 돌아가 봅시다. 일반적으로 쿼리와 키 모두 동일한 벡터 길이(예: d)를 가져야 합니다. q⊤k를 q⊤Mk로 대체하여 쉽게 해결할 수 있지만 여기서 M은 두 공간 사이를 변환하기 위해 적절하게 선택된 행렬입니다. 지금은 dimensions 수가 일치한다고 가정합니다.
In practice, we often think in minibatches for efficiency, such as computing attention for n queries and m key-value pairs, where queries and keys are of length d and values are of length v. The scaled dot-product attention of queries Q∈ℝn×d, keys K∈ℝm×d, and values V∈ℝm×v thus can be written as
실제로 우리는 쿼리와 키의 길이가 d이고 값의 길이가 v인 n queries와 m key-value pairs에 대한 어텐션을 계산하는 것과 같이 효율성을 위해 미니배치를 생각하는 경우가 많습니다. 쿼리의 scaled dot-product attention Q∈ ℝm×v, keys K∈ℝn×d 및 값 K∈ℝm×d는 다음과 같이 쓸 수 있습니다.
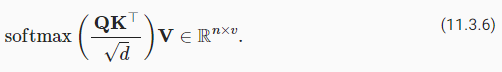
Note that when applying this to a minibatch, we need the batch matrix multiplication introduced in (11.3.5). In the following implementation of the scaled dot product attention, we use dropout for model regularization.
이것을 미니 배치에 적용할 때 (11.3.5)에서 소개한 배치 행렬 곱셈 batch matrix multiplication이 필요합니다. scaled dot product attention의 다음 구현에서는 모델 정규화 model regularization를 위해 dropout 을 사용합니다.
class DotProductAttention(nn.Module): #@save
"""Scaled dot product attention."""
def __init__(self, dropout):
super().__init__()
self.dropout = nn.Dropout(dropout)
# Shape of queries: (batch_size, no. of queries, d)
# Shape of keys: (batch_size, no. of key-value pairs, d)
# Shape of values: (batch_size, no. of key-value pairs, value dimension)
# Shape of valid_lens: (batch_size,) or (batch_size, no. of queries)
def forward(self, queries, keys, values, valid_lens=None):
d = queries.shape[-1]
# Swap the last two dimensions of keys with keys.transpose(1, 2)
scores = torch.bmm(queries, keys.transpose(1, 2)) / math.sqrt(d)
self.attention_weights = masked_softmax(scores, valid_lens)
return torch.bmm(self.dropout(self.attention_weights), values)
이 코드는 스케일 조절된 점곱 어텐션(DotProductAttention)을 구현한 파이토치(nn.Module) 클래스입니다. 어텐션 메커니즘은 주어진 쿼리(queries)와 키(keys)의 쌍에 대한 가중합을 구하는데 사용되며, 자연어 처리 및 시계열 데이터 처리와 같은 다양한 딥러닝 모델에서 사용됩니다.
여기서 어텐션은 다음과 같이 작동합니다:
- 쿼리(queries)와 키(keys)는 주어진 입력에 대한 임베딩입니다.
- 쿼리와 키 간의 점곱을 계산하고, 각 값에 대한 가중치를 얻습니다.
- 가중치는 스케일링된(스케일 조절) 소프트맥스 함수를 통과하여 정규화됩니다.
- 가중치를 값을(values)에 적용하여 어텐션 가중합을 계산합니다.
위 코드에서 forward 함수의 인자들은 다음과 같습니다:
- queries: 쿼리 행렬로, 크기는 (batch_size, no. of queries, d)입니다. 여기서 d는 임베딩 차원을 나타냅니다.
- keys: 키 행렬로, 크기는 (batch_size, no. of key-value pairs, d)입니다.
- values: 값 행렬로, 크기는 (batch_size, no. of key-value pairs, value dimension)입니다. 값 차원은 쿼리와 키에 대한 가중합 후의 결과 차원을 나타냅니다.
- valid_lens: 옵션으로 주어진 유효한 시퀀스 길이입니다. 이를 사용하여 마스킹을 수행합니다.
이어서 코드 내부를 살펴보면, 점곱 어텐션의 연산 과정을 담은 것을 확인할 수 있습니다. 최종적으로 어텐션 가중합을 구하고 이를 값(values)에 적용하여 반환합니다.
torch.bmm() 에 대하여.
The torch.bmm() function in PyTorch stands for "batch matrix-matrix" multiplication. It is used to perform matrix multiplication between two batches of matrices. This function is particularly useful in deep learning, especially in scenarios involving neural networks, where batch operations are common due to the parallel processing capabilities of modern hardware.
torch.bmm() 함수는 파이토치에서 "배치 행렬-행렬" 곱셈을 수행하는 기능입니다. 이 함수는 두 개의 행렬 배치 간의 행렬 곱셈을 수행하는 데 사용됩니다. 특히 현대 하드웨어의 병렬 처리 능력으로 인해 배치 작업이 일반적인 딥 러닝에서 유용하게 사용됩니다.
Here's how torch.bmm() works:
torch.bmm() 함수의 작동 방식은 다음과 같습니다:
- Inputs: It takes two input tensors of shape (batch_size, n, m) and (batch_size, m, p), where batch_size is the number of samples in the batch, and n, m, and p are the dimensions of the matrices.
입력: torch.bmm()은 (batch_size, n, m) 모양과 (batch_size, m, p) 모양의 두 개의 입력 텐서를 가져옵니다. 여기서 batch_size는 배치의 샘플 수이고, n, m, p는 행렬의 차원입니다. - Output: The output of torch.bmm() will be a tensor of shape (batch_size, n, p).
출력: torch.bmm()의 출력은 (batch_size, n, p) 모양의 텐서입니다. - Multiplication: For each batch sample, the function performs matrix multiplication between the corresponding matrices in the two input tensors.
곱셈: 각 배치 샘플에 대해 함수는 두 입력 텐서의 해당 행렬 사이의 행렬 곱셈을 수행합니다.
In other words, torch.bmm() computes the matrix product for each pair of matrices within the batch and stacks the results into an output tensor. This is especially useful when dealing with batches of sequences in sequence-to-sequence models, where each sequence can be represented as a matrix.
Here's a simple example of using torch.bmm():
다시 말해, torch.bmm()은 배치 내 각 행렬 쌍에 대한 행렬 곱셈을 계산하고 결과를 출력 텐서로 스택합니다. 이는 특히 시퀀스 간 변환 모델에서 시퀀스 배치를 다룰 때 유용합니다. 여기 간단한 torch.bmm() 사용 예시가 있습니다:
import torch
batch_size = 2
n = 3
m = 4
p = 2
# 두 개의 배치 행렬 생성
A = torch.randn(batch_size, n, m)
B = torch.randn(batch_size, m, p)
# 배치 행렬-행렬 곱셈 수행
C = torch.bmm(A, B)
print(C.shape) # 출력: torch.Size([2, 3, 2])In this example, A and B are batched matrices with dimensions (2, 3, 4) and (2, 4, 2) respectively. After performing torch.bmm(A, B), the resulting tensor C will have dimensions (2, 3, 2), which corresponds to the batch size, number of rows, and number of columns of the multiplied matrices.
이 예제에서 A와 B는 각각 (2, 3, 4)와 (2, 4, 2) 차원의 배치 행렬입니다. torch.bmm(A, B)를 수행한 후 결과 텐서 C는 차원이 (2, 3, 2)이며 이는 배치 크기, 행의 개수 및 열의 개수에 해당합니다.
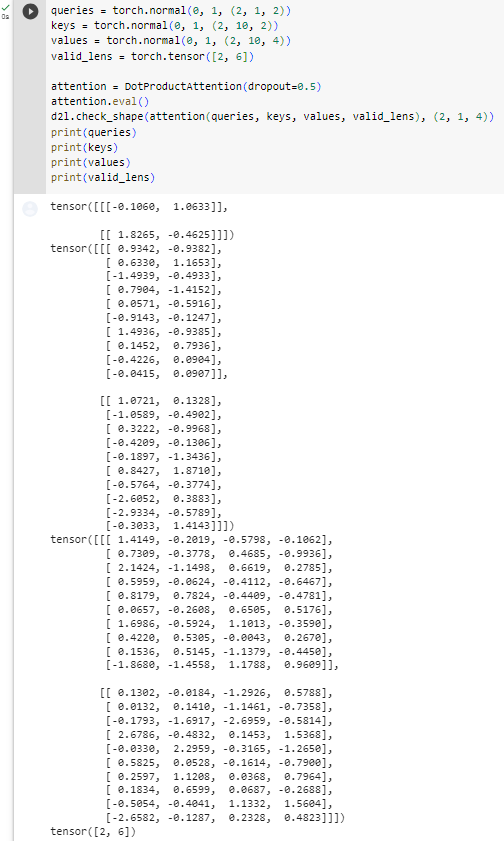
To illustrate how the DotProductAttention class works, we use the same keys, values, and valid lengths from the earlier toy example for additive attention. For the purpose of our example we assume that we have a minibatch size of 2, a total of 10 keys and values, and that the dimensionality of the values is 4. Lastly, we assume that the valid length per observation is 2 and 6 respectively. Given that, we expect the output to be a 2×1×4 tensor, i.e., one row per example of the minibatch.
DotProductAttention 클래스의 작동 방식을 설명하기 위해 추가 주의를 위해 이전 toy example와 동일한 키, 값 및 유효한 길이를 사용합니다. 예제의 목적을 위해 미니배치 크기가 2이고 총 10개의 키와 값이 있고 값의 차원이 4라고 가정합니다. 마지막으로 관찰당 유효한 길이는 각각 2와 6이라고 가정합니다. . 이를 감안할 때 출력이 2×1×4 텐서, 즉 미니배치의 예당 하나의 행이 될 것으로 예상합니다.
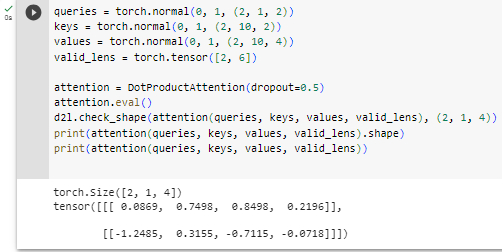
queries = torch.normal(0, 1, (2, 1, 2))
keys = torch.normal(0, 1, (2, 10, 2))
values = torch.normal(0, 1, (2, 10, 4))
valid_lens = torch.tensor([2, 6])
attention = DotProductAttention(dropout=0.5)
attention.eval()
d2l.check_shape(attention(queries, keys, values, valid_lens), (2, 1, 4))위 코드는 DotProductAttention 클래스를 사용하여 어텐션 메커니즘을 시연하는 예시입니다. 주어진 쿼리(queries), 키(keys), 값(values), 그리고 유효한 시퀀스 길이(valid_lens)로부터 어텐션 결과를 계산하고 그 크기를 확인하는 과정을 보여줍니다.
여기서 주어진 텐서들은 다음과 같습니다:
- queries: 쿼리 행렬로, 크기는 (2, 1, 2)입니다. 두 개의 쿼리가 있고, 각 쿼리의 임베딩 차원은 2입니다.
- keys: 키 행렬로, 크기는 (2, 10, 2)입니다. 두 개의 쿼리에 대해 10개의 키가 있으며, 각 키의 임베딩 차원은 2입니다.
- values: 값 행렬로, 크기는 (2, 10, 4)입니다. 두 개의 쿼리에 대해 10개의 값이 있으며, 각 값의 차원은 4입니다.
- valid_lens: 유효한 시퀀스 길이로, 크기는 (2,6)입니다. 각 쿼리에 대한 유효한 길이가 포함되어 있습니다.
이어서 DotProductAttention 클래스를 초기화하고, eval() 메서드를 호출하여 드롭아웃을 비활성화합니다. 그리고 이 클래스를 이용하여 주어진 입력으로 어텐션을 수행하고 그 결과의 크기를 d2l.check_shape 함수를 통해 확인합니다. 이를 통해 어텐션 결과의 크기가 예상한 것과 일치하는지 검증하는 것이 목적입니다.
Pytorch에서 eval() 메소드란?
eval()은 PyTorch 모델의 메서드 중 하나로, 모델을 평가 모드로 설정하는 역할을 합니다. 평가 모드로 설정되면 모델 내부에서 발생하는 일부 동작이 변경되어 학습 중에만 사용되는 요소들을 비활성화하거나 조정합니다.
일반적으로 학습 중에 사용되는 요소 중에는 드롭아웃(Dropout)과 배치 정규화(Batch Normalization)이 있습니다. 드롭아웃은 학습 중에 일부 뉴런을 무작위로 비활성화하여 과적합을 방지하는데 사용됩니다. 배치 정규화는 배치 단위로 입력 데이터의 평균과 분산을 조정하여 학습을 안정화하는 역할을 합니다.
eval()을 호출하면 모델 내부의 드롭아웃과 배치 정규화 등 학습 중에만 활성화되는 부분들이 비활성화됩니다. 이로써 모델의 평가 결과가 학습 결과와 일관성을 유지하게 되며, 실제 평가나 추론에 사용될 때의 모델 동작을 정확하게 반영할 수 있습니다.
예를 들어, 위에서 설명한 코드에서 attention.eval()을 호출한 이유는 모델의 학습 시에 사용되는 드롭아웃을 비활성화하여 평가 모드에서도 일관된 결과를 얻기 위함입니다.
Let’s check whether the attention weights actually vanish for anything beyond the second and sixth column respectively (due to setting valid length to 2 and 6).
유효 길이를 2와 6으로 설정했기 때문에 각각 두 번째와 여섯 번째 열을 넘어서는 어텐션 가중치가 실제로 사라지는지 확인해 봅시다.
d2l.show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)),
xlabel='Keys', ylabel='Queries')위 코드는 주어진 DotProductAttention 모델의 어텐션 가중치(attention weights)를 시각화하여 히트맵으로 나타내는 작업을 수행합니다.
show_heatmaps 함수는 매트릭스 형태의 데이터를 입력으로 받아서 히트맵으로 시각화해주는 함수입니다. 이를 통해 어텐션 가중치를 시각화하면 어떤 키(key)가 어떤 쿼리(query)에 얼마나 중요한지를 확인할 수 있습니다.
attention.attention_weights는 어텐션 메커니즘을 통해 계산된 각 쿼리에 대한 키의 가중치입니다. 이를 통해 어텐션 가중치를 show_heatmaps 함수에 넣어 시각화하면, 행이 쿼리(Query)를, 열이 키(Keys)를 나타내는 히트맵이 생성됩니다. 각 히트맵 셀의 색상이 진할수록 해당 키가 해당 쿼리에 높은 가중치를 부여한 것을 의미합니다.



11.3.4. Additive Attention
When queries q and keys k are vectors of different dimensionalities, we can either use a matrix to address the mismatch via q⊤Mk, or we can use additive attention as the scoring function. Another benefit is that, as its name indicates, the attention is additive. This can lead to some minor computational savings. Given a query q∈ℝq and a key k∈ℝk, the additive attention scoring function (Bahdanau et al., 2014) is given by
쿼리 q와 키 k가 서로 다른 차원의 벡터인 경우 행렬을 사용하여 q⊤Mk를 통해 불일치를 해결하거나 additive attention를 scoring function로 사용할 수 있습니다. 또 다른 이점은 이름에서 알 수 있듯이 attention is additive라는 것입니다. 이것은 약간의 계산 절감으로 이어질 수 있습니다. 쿼리 q∈ℝq와 키 k∈ℝk가 주어지면 additive attention scoring function(Bahdanau et al., 2014)는 다음과 같이 제공됩니다.

where Wq∈ℝℎ×q, Wk∈ℝℎ×k, and wv∈ℝℎ are the learnable parameters. This term is then fed into a softmax to ensure both nonnegativity and normalization. An equivalent interpretation of (11.3.7) is that the query and key are concatenated and fed into an MLP with a single hidden layer. Using tanh as the activation function and disabling bias terms, we implement additive attention as follows:
여기서 Wq∈ℝℎ×q, Wk∈ℝℎ×k 및 wv∈ℝℎ는 learnable parameters입니다. 그런 다음 이 term 을 소프트맥스에 입력하여 nonnegativity 과 normalization를 모두 보장합니다. (11.3.7)의 equivalent interpretation은 쿼리와 키가 연결되어 단일 숨겨진 레이어가 있는 MLP에 공급된다는 것입니다. tanh를 활성화 함수로 사용하고 bias terms을 비활성화하여 다음과 같이 additive attention를 구현합니다.
class AdditiveAttention(nn.Module): #@save
"""Additive attention."""
def __init__(self, num_hiddens, dropout, **kwargs):
super(AdditiveAttention, self).__init__(**kwargs)
self.W_k = nn.LazyLinear(num_hiddens, bias=False)
self.W_q = nn.LazyLinear(num_hiddens, bias=False)
self.w_v = nn.LazyLinear(1, bias=False)
self.dropout = nn.Dropout(dropout)
def forward(self, queries, keys, values, valid_lens):
queries, keys = self.W_q(queries), self.W_k(keys)
# After dimension expansion, shape of queries: (batch_size, no. of
# queries, 1, num_hiddens) and shape of keys: (batch_size, 1, no. of
# key-value pairs, num_hiddens). Sum them up with broadcasting
features = queries.unsqueeze(2) + keys.unsqueeze(1)
features = torch.tanh(features)
# There is only one output of self.w_v, so we remove the last
# one-dimensional entry from the shape. Shape of scores: (batch_size,
# no. of queries, no. of key-value pairs)
scores = self.w_v(features).squeeze(-1)
self.attention_weights = masked_softmax(scores, valid_lens)
# Shape of values: (batch_size, no. of key-value pairs, value
# dimension)
return torch.bmm(self.dropout(self.attention_weights), values)위 코드는 AdditiveAttention 클래스를 정의하는 파이토치 모듈입니다. 이 클래스는 추가적인 어텐션 메커니즘을 구현한 것으로, 주어진 쿼리(query)와 키(key)를 이용하여 가중치를 계산하여 값을 어텐션을 통해 결합하는 과정을 수행합니다.
- __init__: 클래스 생성자로, 초기화를 위한 함수입니다. 여기서는 nn.LazyLinear 레이어를 이용하여 가중치 매개변수를 정의합니다. 쿼리와 키에 각각 W_q와 W_k 매개변수를 통과시키고, 가중치 값을 계산할 때 w_v 매개변수를 이용합니다.
- forward: 클래스의 순전파 연산을 정의하는 함수입니다. 주어진 쿼리와 키에 각각 W_q와 W_k를 적용하여 차원을 변환하고, 차원을 확장하여 쿼리와 키를 더합니다. 그 후에는 tanh 함수를 이용하여 활성화 값을 생성하고, 이 값을 w_v 매개변수에 통과시켜 가중치 스코어를 계산합니다. 마지막으로, 어텐션 가중치를 정규화한 후, 해당 가중치를 값을 어텐션을 통해 결합하여 반환합니다.
이러한 방식으로, AdditiveAttention 클래스는 쿼리와 키의 특성을 추가하여 어텐션 가중치를 계산하고, 이를 사용하여 값을 어텐션을 통해 결합합니다.
class AdditiveAttention(nn.Module): #@save
"""Additive attention."""
def __init__(self, num_hiddens, dropout, **kwargs):
super(AdditiveAttention, self).__init__(**kwargs)
self.W_k = nn.LazyLinear(num_hiddens, bias=False)
self.W_q = nn.LazyLinear(num_hiddens, bias=False)
self.w_v = nn.LazyLinear(1, bias=False)
self.dropout = nn.Dropout(dropout)- AdditiveAttention 클래스를 정의하고 있습니다. 이 클래스는 파이토치의 nn.Module을 상속받습니다.
- 클래스의 생성자(__init__)에서는 어텐션에 사용되는 파라미터와 레이어들을 초기화하고 있습니다.
- num_hiddens는 은닉 차원의 크기입니다.
- dropout은 드롭아웃 비율을 나타냅니다.
- **kwargs는 키워드 인수를 받을 수 있도록 합니다.
- nn.LazyLinear은 선형 레이어를 생성합니다. W_k, W_q, w_v는 각각 키, 쿼리, 값을 위한 레이어입니다.
def forward(self, queries, keys, values, valid_lens):
queries, keys = self.W_q(queries), self.W_k(keys)
features = queries.unsqueeze(2) + keys.unsqueeze(1)
features = torch.tanh(features)
scores = self.w_v(features).squeeze(-1)
self.attention_weights = masked_softmax(scores, valid_lens)
return torch.bmm(self.dropout(self.attention_weights), values)- forward 메서드는 어텐션 연산을 수행하는 메서드입니다.
- queries, keys, values는 어텐션 연산에 사용될 쿼리, 키, 값입니다.
- W_q와 W_k를 각각 queries와 keys에 적용하여 차원 변환을 수행합니다.
- unsqueeze를 사용하여 쿼리와 키의 차원을 확장하여 덧셈이 가능한 형태로 변환합니다.
- tanh 함수를 적용하여 활성화 값을 생성합니다.
- w_v를 사용하여 어텐션 스코어를 계산하고, 마지막 차원을 제거하여 scores를 얻습니다.
- masked_softmax 함수를 사용하여 어텐션 가중치를 계산합니다.
- self.attention_weights에 어텐션 가중치를 저장합니다.
- 최종적으로 어텐션 가중치를 이용하여 값들을 결합한 결과를 반환합니다.
이렇게 정의된 AdditiveAttention 클래스는 입력된 쿼리와 키를 이용하여 어텐션 가중치를 계산하고, 이를 사용하여 값들을 결합하는 과정을 수행합니다.
Let’s see how AdditiveAttention works. In our toy example we pick queries, keys and values of size (2,1,20), (2,10,2) and (2,10,4), respectively. This is identical to our choice for DotProductAttention, except that now the queries are 20-dimensional. Likewise, we pick (2,6) as the valid lengths for the sequences in the minibatch.
AdditiveAttention이 어떻게 작동하는지 살펴보겠습니다. 우리의 toy example에서는 크기가 각각 (2,1,20), (2,10,2) 및 (2,10,4)인 쿼리, 키 및 값을 선택합니다. 이제 쿼리가 20차원이라는 점을 제외하면 DotProductAttention에 대한 선택과 동일합니다. 마찬가지로 미니배치의 시퀀스에 유효한 길이로 (2,6)을 선택합니다.
queries = torch.normal(0, 1, (2, 1, 20))
attention = AdditiveAttention(num_hiddens=8, dropout=0.1)
attention.eval()
d2l.check_shape(attention(queries, keys, values, valid_lens), (2, 1, 4))- 위 코드는 AdditiveAttention 클래스를 사용하여 어텐션 연산을 수행하는 예시입니다.
- queries는 (batch_size, no. of queries, d) 형태의 입력 쿼리 텐서입니다. 이 예시에서는 크기가 (2, 1, 20)인 텐서를 사용합니다.
- attention 객체는 AdditiveAttention 클래스의 인스턴스입니다.
- attention.eval()은 모델을 평가 모드로 설정하는 메서드입니다. 드롭아웃 등의 영향을 받지 않습니다.
- attention(queries, keys, values, valid_lens)는 AdditiveAttention 클래스의 forward 메서드를 호출하여 어텐션 연산을 수행합니다. 여기서 keys, values, valid_lens는 정의되지 않았지만, 이전에 정의된 값들을 사용하는 것으로 가정합니다.
- d2l.check_shape는 계산된 결과의 형태를 확인하는 메서드입니다. 이 코드에서는 결과의 형태가 (2, 1, 4)인지 확인하고 있습니다.
When reviewing the attention function we see a behavior that is qualitatively quite similar to that from DotProductAttention. That is, only terms within the chosen valid length (2,6) are nonzero.
attention function을 검토할 때 DotProductAttention의 동작과 질적으로 매우 유사한 동작을 볼 수 있습니다. 즉, 선택한 유효 길이(2,6) 내의 항만 0이 아닙니다.
d2l.show_heatmaps(attention.attention_weights.reshape((1, 1, 2, 10)),
xlabel='Keys', ylabel='Queries')- 위 코드는 어텐션 가중치를 시각화하는 예시입니다.
- d2l.show_heatmaps 함수는 히트맵을 시각화하는 함수입니다.
- attention.attention_weights는 어텐션 가중치를 나타내는 텐서입니다. 이 값은 이전에 정의된 어텐션 연산을 통해 계산된 것으로 가정합니다.
- attention.attention_weights.reshape((1, 1, 2, 10))는 어텐션 가중치를 히트맵으로 표시하기 위해 형태를 재구성하는 것입니다. 여기서 (1, 1, 2, 10)은 히트맵 형태를 지정하고 있습니다. 첫 번째 차원은 배치 크기를 나타내며, 두 번째 차원은 어텐션 쿼리의 개수, 세 번째 차원은 어텐션 키의 개수, 네 번째 차원은 키의 특성 개수를 나타냅니다.
- xlabel과 ylabel은 각각 x축과 y축의 라벨을 지정하는 매개변수입니다.
- 결과적으로, 어텐션 가중치를 히트맵으로 시각화하여 키와 쿼리 간의 관련성을 확인할 수 있습니다.



11.3.5. Summary
In this section we introduced the two key attention scoring functions: dot product and additive attention. They are effective tools for aggregating across sequences of variable length. In particular, the dot product attention is the mainstay of modern Transformer architectures. When queries and keys are vectors of different lengths, we can use the additive attention scoring function instead. Optimizing these layers is one of the key areas of advance in recent years. For instance, Nvidia’s Transformer Library and Megatron (Shoeybi et al., 2019) crucially rely on efficient variants of the attention mechanism. We will dive into this in quite a bit more detail as we review Transformers in later sections.
이 섹션에서는 두 가지 주요 attention scoring functions인 dot product 및 additive attention을 소개했습니다. 가변 길이의 시퀀스를 집계하는 데 효과적인 도구입니다. 특히 ***dot product attention***은 현대 트랜스포머 아키텍처의 중심입니다. 쿼리와 키가 길이가 다른 벡터인 경우 additive attention scoring function을 대신 사용할 수 있습니다. 이러한 계층을 최적화하는 것은 최근 몇 년간 발전의 핵심 영역 중 하나입니다. 예를 들어 Nvidia의 Transformer Library와 Megatron(Shoeybi et al., 2019)은 어텐션 메커니즘의 efficient variants에 결정적으로 의존합니다. 이후 섹션에서 트랜스포머를 검토하면서 이에 대해 좀 더 자세히 살펴보겠습니다.
attention scoring functions 란?
'어텐션 스코어 함수(Attention Scoring Function)'는 어텐션 메커니즘에서 사용되는 핵심 요소 중 하나입니다. 이 함수는 쿼리(Query)와 키(Key) 간의 관련성을 계산하여 어텐션 가중치(Attention Weights)를 생성합니다. 어텐션 스코어 함수는 주어진 쿼리와 키의 조합에 대해 얼마나 관련성이 높은지를 측정하여 어텐션 가중치를 결정하는 역할을 합니다.
어텐션 스코어 함수의 목적은 쿼리와 키 간의 유사도를 정량화하여 어텐션 가중치를 생성하는 것입니다. 이렇게 생성된 어텐션 가중치는 값이 높을수록 해당 키가 해당 쿼리에 더 많은 영향을 미치도록 하는 역할을 합니다. 어텐션 스코어 함수는 다양한 형태와 방식으로 정의될 수 있으며, 이는 어텐션 메커니즘의 종류에 따라 달라질 수 있습니다.
어텐션 스코어 함수는 주로 내적(Dot Product), 유클리디안 거리(Euclidean Distance), 맨하탄 거리(Manhattan Distance), 다양한 커널 함수(Kernel Function) 등을 활용하여 구현될 수 있습니다. 이 함수의 선택은 어텐션 메커니즘의 성능과 특성에 영향을 미칩니다.
Dot Product란?
'닷 프로덕트(Dot Product)'는 두 벡터 사이에서 각 성분을 곱한 후 그 결과를 더한 값을 나타내는 연산입니다. 두 벡터의 내적(Dot Product)이라고도 불립니다. 닷 프로덕트는 벡터 간의 유사도, 방향, 정사영 등을 계산하는 데 사용됩니다.
두 벡터 A와 B의 닷 프로덕트는 다음과 같이 표현됩니다:
여기서 와 는 각 벡터 A와 B의 번째 성분을 나타냅니다. 닷 프로덕트의 결과는 스칼라 값으로 나타납니다.
닷 프로덕트는 다양한 분야에서 사용되며, 특히 선형 대수학, 머신 러닝, 신경망 등에서 많이 활용됩니다. 벡터의 내적이나 유사도 측정, 정사영 등 다양한 개념과 연관되어 사용됩니다.
Dot product attention이란?
'Dot Product Attention'은 어텐션 메커니즘 중 하나로, 입력된 쿼리(Query)와 키(Key) 간의 내적(점곱)을 통해 유사도를 계산하여 어텐션 가중치를 생성하는 방식입니다. 이 방법은 입력된 쿼리와 키의 유사성을 측정하는 과정에서 내적 연산을 활용하여 어텐션 가중치를 계산합니다.
'Dot Product Attention'의 주요 특징은 다음과 같습니다:
- 내적 연산: 쿼리와 키의 벡터를 내적 연산으로 곱하여 유사도를 계산합니다. 내적은 벡터의 방향성을 고려하는 연산으로, 유사한 방향성을 가지는 벡터일수록 더 높은 유사도 값을 얻게 됩니다.
- 활성화 함수: 내적 연산을 통해 계산된 유사도 값을 활성화 함수(일반적으로 소프트맥스)를 사용하여 정규화하여 어텐션 가중치를 생성합니다.
- 출력 계산: 어텐션 가중치와 키 벡터를 가중합하여 출력 벡터를 생성합니다.
'Dot Product Attention'은 계산이 간단하고 효과적으로 유사도를 측정할 수 있어서 주로 자연어 처리(NLP) 분야에서 사용되며, 특히 트랜스포머(Transformer) 모델의 어텐션 메커니즘에 많이 활용됩니다.
Additive Attention 이란?
'Additive Attention'은 쿼리(Query)와 키(Key)가 서로 다른 차원을 가지는 경우에 사용되는 어텐션 메커니즘입니다. 이 메커니즘은 쿼리와 키 간의 차원을 일치시키기 위해 가산(Additive) 함수를 사용하여 어텐션 스코어를 계산합니다.
일반적인 어텐션 메커니즘에서는 쿼리와 키가 동일한 차원을 가지며 내적(Dot Product) 또는 유사도 함수를 통해 어텐션 점수를 계산합니다. 하지만 'Additive Attention'에서는 쿼리와 키의 차원이 다르므로, 이를 일치시키기 위해 선형 변환과 활성화 함수를 사용하여 어텐션 스코어를 생성합니다.
일반적으로 'Additive Attention'은 다음과 같은 단계로 이루어집니다:
- 쿼리와 키를 각각 선형 변환하여 차원을 맞춥니다.
- 각 변환된 쿼리와 키 간의 유사도를 계산합니다.
- 계산된 유사도에 활성화 함수(예: 하이퍼볼릭 탄젠트)를 적용하여 어텐션 스코어를 생성합니다.
- 어텐션 스코어를 정규화하고 가중합하여 최종 어텐션 출력을 계산합니다.
'Additive Attention'은 특히 트랜스포머 아키텍처에서 사용되는 어텐션 메커니즘 중 하나로, 입력의 다른 부분 간의 상관 관계를 모델링하고 시퀀스 정보를 캡처하는 데 사용됩니다.
11.3.6. Exercises
- Implement distance-based attention by modifying the DotProductAttention code. Note that you only need the squared norms of the keys ‖ki‖2 for an efficient implementation.
- Modify the dot product attention to allow for queries and keys of different dimensionalities by employing a matrix to adjust dimensions.
- How does the computational cost scale with the dimensionality of the keys, queries, values, and their number? What about the memory bandwidth requirements?
'Dive into Deep Learning > D2L Attention Mechanisms and Transformer' 카테고리의 다른 글
| D2L - 11.9. Large-Scale Pretraining with Transformers (0) | 2023.08.10 |
|---|---|
| D2L - 11.8. Transformers for Vision (0) | 2023.08.10 |
| D2L - 11.7. The Transformer Architecture (0) | 2023.08.09 |
| D2L - 11.6. Self-Attention and Positional Encoding (0) | 2023.08.09 |
| D2L - 11.5. Multi-Head Attention (0) | 2023.08.08 |
| D2L - 11.4. The Bahdanau Attention Mechanism (1) | 2023.08.08 |
| D2L - 11.2. Attention Pooling by Similarity (0) | 2023.08.06 |
| D2L - 11.1. Queries, Keys, and Values (0) | 2023.08.05 |
| D2L - 11. Attention Mechanisms and Transformers (0) | 2023.08.03 |

