https://d2l.ai/chapter_linear-classification/softmax-regression-scratch.html
4.4. Softmax Regression Implementation from Scratch — Dive into Deep Learning 1.0.0-beta0 documentation
d2l.ai
4.4. Softmax Regression Implementation from Scratch
Because softmax regression is so fundamental, we believe that you ought to know how to implement it yourself. Here, we limit ourselves to defining the softmax-specific aspects of the model and reuse the other components from our linear regression section, including the training loop.
softmax regression (회귀)는 매우 기본적이므로 직접 구현하는 방법을 알아야 한다고 생각합니다. 여기서는 모델의 softmax-specific 측면을 정의하는 것으로 제한하고 training loop-교육 루프-를 포함하여 linear regression-선형 회귀- 섹션의 다른 구성 요소를 재사용합니다.
import torch
from d2l import torch as d2l
- import torch: PyTorch 라이브러리를 임포트합니다. 이를 통해 PyTorch의 기능을 사용할 수 있습니다.
- from d2l import torch as d2l: "d2l"이라는 이름의 패키지에서 "torch" 모듈을 임포트합니다. "d2l"은 Dive into Deep Learning (D2L) 도서의 교재와 관련된 유틸리티 함수와 모듈을 제공하는 패키지입니다. 이를 통해 D2L의 편리한 함수와 기능을 사용할 수 있습니다.
이 코드는 PyTorch를 사용하기 위해 torch 모듈을 임포트하고, D2L의 유틸리티 함수와 기능을 사용하기 위해 d2l 모듈을 임포트하는 역할을 합니다.
4.4.1. The Softmax
Let’s begin with the most important part: the mapping from scalars to probabilities. For a refresher, recall the operation of the sum operator along specific dimensions in a tensor, as discussed in Section 2.3.6 and Section 2.3.7. Given a matrix X we can sum over all elements (by default) or only over elements in the same axis. The axis variable lets us compute row and column sums:
가장 중요한 부분인 스칼라에서 확률로의 매핑부터 시작하겠습니다. 복습을 위해 섹션 2.3.6 및 섹션 2.3.7에서 설명한 대로 텐서의 특정 차원에 따른 합계 연산자의 작업을 상기하십시오. 행렬 X가 주어지면 모든 요소(기본값) 또는 동일한 축의 요소에 대해서만 합산할 수 있습니다. 축 변수를 사용하면 행과 열 합계를 계산할 수 있습니다.
X = torch.tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])
X.sum(0, keepdims=True), X.sum(1, keepdims=True)- X = torch.tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]]): 입력 데이터인 X를 정의합니다. 이 예제에서는 크기가 2x3인 텐서입니다. 첫 번째 행은 [1.0, 2.0, 3.0]이고, 두 번째 행은 [4.0, 5.0, 6.0]입니다.
- X.sum(0, keepdims=True): 열 방향으로 합계를 계산합니다. 0은 열 방향을 나타내는 축입니다. keepdims=True는 결과의 차원을 입력과 동일하게 유지하도록 지정합니다. 따라서 결과는 1x3 크기의 텐서가 됩니다. 열 방향으로 각 열의 원소를 합산한 결과입니다.
- X.sum(1, keepdims=True): 행 방향으로 합계를 계산합니다. 1은 행 방향을 나타내는 축입니다. keepdims=True는 결과의 차원을 입력과 동일하게 유지하도록 지정합니다. 따라서 결과는 2x1 크기의 텐서가 됩니다. 행 방향으로 각 행의 원소를 합산한 결과입니다.
이 코드는 주어진 입력 텐서 X에서 열 방향과 행 방향으로 합계를 계산하는 예제입니다. 결과는 각각 1x3 크기와 2x1 크기의 텐서로 출력됩니다.

Computing the softmax requires three steps: (i) exponentiation of each term; (ii) a sum over each row to compute the normalization constant for each example; (iii) division of each row by its normalization constant, ensuring that the result sums to 1.
softmax를 계산하려면 세 단계가 필요합니다. (i) 각 항의 거듭제곱; (ii) 각 예에 대한 정규화 상수를 계산하기 위한 각 행에 대한 합계; (iii) 각 행을 정규화 상수로 나누어 결과 합계가 1이 되도록 합니다.
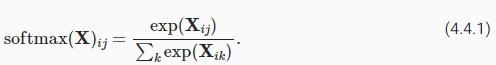
The (logarithm of the) denominator is called the (log) partition function. It was introduced in statistical physics to sum over all possible states in a thermodynamic ensemble. The implementation is straightforward:
분모(의 로그)를 (log) partition function(로그) 분할 함수라고 합니다. thermodynamic ensemble.열역학적 앙상블에서 가능한 모든 상태를 합산하기 위해 statistical physics 통계 물리학에 도입되었습니다. 구현은 간단합니다.
def softmax(X):
X_exp = torch.exp(X)
partition = X_exp.sum(1, keepdims=True)
return X_exp / partition # The broadcasting mechanism is applied here
- def softmax(X):: softmax라는 함수를 정의합니다. 이 함수는 입력으로 주어진 텐서 X에 softmax 함수를 적용하여 반환합니다.
- X_exp = torch.exp(X): 입력 텐서 X의 각 원소에 대해 지수 함수를 계산하여 X_exp에 저장합니다. 이는 softmax 함수의 분자 부분입니다.
- partition = X_exp.sum(1, keepdims=True): X_exp의 행 방향으로 합계를 계산하여 partition에 저장합니다. keepdims=True는 결과의 차원을 입력과 동일하게 유지하도록 지정합니다. 이는 softmax 함수의 분모 부분입니다.
- return X_exp / partition: 분자인 X_exp를 분모인 partition으로 나누어 softmax 함수의 결과를 반환합니다. 이 부분에서 브로드캐스팅 메커니즘이 적용됩니다. X_exp와 partition의 차원이 서로 다르더라도 알아서 확장되어 계산됩니다.
이 코드는 입력 텐서에 softmax 함수를 적용하는 함수를 정의한 것입니다. softmax 함수는 입력 텐서의 각 원소를 지수 함수로 변환한 후, 행 방향으로 합계를 계산하여 각 원소를 분모로 나누어 확률 분포를 생성합니다.
For any input X, we turn each element into a non-negative number. Each row sums up to 1, as is required for a probability. Caution: the code above is not robust against very large or very small arguments. While this is sufficient to illustrate what is happening, you should not use this code verbatim for any serious purpose. Deep learning frameworks have such protections built-in and we will be using the built-in softmax going forward.
모든 입력 X에 대해 각 요소를 음수가 아닌 숫자로 바꿉니다. 확률에 필요하므로 각 행의 합계는 1이 됩니다. 주의: 위의 코드는 매우 크거나 매우 작은 인수에 대해 강력하지 않습니다. 이는 무슨 일이 일어나고 있는지 설명하기에 충분하지만 심각한 목적을 위해 이 코드를 그대로 사용해서는 안 됩니다. 딥 러닝 프레임워크에는 이러한 보호 기능이 내장되어 있으며 앞으로도 내장된 softmax를 사용할 것입니다.
X = torch.rand((2, 5))
X_prob = softmax(X)
X_prob, X_prob.sum(1)
- X = torch.rand((2, 5)): 2x5 크기의 랜덤한 값을 가진 텐서 X를 생성합니다.
- X_prob = softmax(X): 앞서 설명한 softmax 함수를 X에 적용하여 확률 분포를 생성하여 X_prob에 저장합니다. X의 각 행은 확률로 변환됩니다.
- X_prob: X_prob를 출력합니다. 이는 각 행이 확률로 변환된 텐서입니다.
- X_prob.sum(1): X_prob의 행 방향으로 합계를 계산하여 출력합니다. 이를 통해 각 행의 원소들의 합이 1인지 확인할 수 있습니다.
이 코드는 주어진 입력 X에 softmax 함수를 적용하여 확률 분포를 생성하는 예시입니다. X는 랜덤한 값으로 초기화된 텐서이며, softmax 함수를 통해 각 행의 값을 확률로 변환합니다. X_prob은 확률로 변환된 텐서이며, X_prob.sum(1)을 통해 각 행의 원소들의 합이 1인지 확인할 수 있습니다.

4.4.2. The Model
We now have everything that we need to implement the softmax regression model. As in our linear regression example, each instance will be represented by a fixed-length vector. Since the raw data here consists of 28×28 pixel images, we flatten each image, treating them as vectors of length 784. In later chapters, we will introduce convolutional neural networks, which exploit the spatial structure in a more satisfying way.
이제 softmax 회귀(regression ) 모델을 구현하는 데 필요한 모든 것이 있습니다. linear regression 선형 회귀 예제에서와 같이 각 인스턴스는 fixed-length vector-고정 길이 벡터-로 표시됩니다. 여기서 원시 데이터는 28X28 픽셀 이미지로 구성되어 있으므로 각 이미지를 평면화하여 길이가 784인 벡터로 취급합니다. 이후 장에서는 공간 구조를 보다 만족스럽게 활용하는 convolutional neural networks-컨벌루션 신경망-을 소개합니다.
In softmax regression, the number of outputs from our network should be equal to the number of classes. Since our dataset has 10 classes, our network has an output dimension of 10. Consequently, our weights constitute a 784×10 matrix plus a 1×10 dimensional row vector for the biases. As with linear regression, we initialize the weights W with Gaussian noise. The biases are initialized as zeros.
softmax 회귀에서 네트워크의 출력 수는 클래스 수와 같아야 합니다. 데이터 세트에 10개의 클래스가 있으므로 네트워크의 출력 차원은 10입니다. 결과적으로 가중치는 편향에 대한 1X10 차원 행 벡터와 784 X 10 행렬을 구성합니다. linear regression-선형 회귀-와 마찬가지로 가중치 W를 Gaussian noise-가우시안 노이즈-로 초기화합니다. biases -편향-은 0으로 초기화됩니다.
class SoftmaxRegressionScratch(d2l.Classifier):
def __init__(self, num_inputs, num_outputs, lr, sigma=0.01):
super().__init__()
self.save_hyperparameters()
self.W = torch.normal(0, sigma, size=(num_inputs, num_outputs),
requires_grad=True)
self.b = torch.zeros(num_outputs, requires_grad=True)
def parameters(self):
return [self.W, self.b]- class SoftmaxRegressionScratch(d2l.Classifier): SoftmaxRegressionScratch 클래스를 정의합니다. 이 클래스는 d2l.Classifier 클래스를 상속받습니다.
- def __init__(self, num_inputs, num_outputs, lr, sigma=0.01): 클래스의 초기화 메서드입니다. 입력으로 num_inputs (입력 특성의 수), num_outputs (클래스의 수), lr (학습률), sigma (가중치 초기화를 위한 표준 편차)를 받습니다.
- super().__init__(): 상위 클래스인 d2l.Classifier의 초기화 메서드를 호출합니다.
- self.save_hyperparameters(): 하이퍼파라미터를 저장합니다.
- self.W = torch.normal(0, sigma, size=(num_inputs, num_outputs), requires_grad=True): 크기가 (num_inputs, num_outputs)인 가중치 행렬 self.W를 생성합니다. 가중치는 평균이 0이고 표준 편차가 sigma인 정규 분포로부터 무작위로 초기화되며, requires_grad=True를 설정하여 역전파를 통해 학습될 수 있도록 설정합니다.
- self.b = torch.zeros(num_outputs, requires_grad=True): 길이가 num_outputs인 편향 벡터 self.b를 생성합니다. 모든 요소가 0인 초기값으로 설정되며, requires_grad=True를 설정하여 역전파를 통해 학습될 수 있도록 설정합니다.
- def parameters(self): 모델의 학습 가능한 파라미터를 반환하는 메서드입니다. self.W와 self.b를 리스트로 묶어 반환합니다.
이 코드는 Softmax 회귀 모델을 Scratch에서 구현한 클래스입니다. SoftmaxRegressionScratch 클래스는 d2l.Classifier를 상속받으며, 가중치와 편향을 초기화하고 학습 가능한 파라미터를 반환하는 기능을 포함하고 있습니다. 이 클래스를 사용하여 Softmax 회귀 모델을 구현하고 학습시킬 수 있습니다.
The code below defines how the network maps each input to an output. Note that we flatten each 28×28 pixel image in the batch into a vector using reshape before passing the data through our model.
아래 코드는 네트워크가 각 입력을 출력에 매핑하는 방법을 정의합니다. 모델을 통해 데이터를 전달하기 전에 reshape를 사용하여 배치의 각 28 X 28 픽셀 이미지를 벡터로 병합합니다.
@d2l.add_to_class(SoftmaxRegressionScratch)
def forward(self, X):
X = X.reshape((-1, self.W.shape[0]))
return softmax(torch.matmul(X, self.W) + self.b)이 코드는 SoftmaxRegressionScratch 클래스에 forward 메서드를 추가하는 부분입니다. 코드를 한 줄씩 설명해드리겠습니다.
- @d2l.add_to_class(SoftmaxRegressionScratch): d2l.add_to_class 데코레이터를 사용하여 SoftmaxRegressionScratch 클래스에 메서드를 추가합니다.
- def forward(self, X): forward 메서드를 정의합니다. 이 메서드는 입력 데이터 X를 받습니다.
- X = X.reshape((-1, self.W.shape[0])): 입력 데이터 X를 크기가 (배치 크기, 입력 특성의 수)인 형태로 변형합니다. 이를 통해 배치 처리가 가능하도록 준비합니다.
- return softmax(torch.matmul(X, self.W) + self.b): 입력 데이터 X와 가중치 행렬 self.W 그리고 편향 벡터 self.b를 사용하여 Softmax 함수를 적용한 결과를 반환합니다. 입력 데이터와 가중치 행렬을 행렬 곱셈한 후 편향 벡터를 더한 다음, 이를 Softmax 함수에 적용하여 예측값을 계산합니다.
이렇게 forward 메서드를 추가하여 입력 데이터에 대한 예측값을 계산할 수 있게 되었습니다. 이 메서드를 사용하여 Softmax 회귀 모델을 구현한 SoftmaxRegressionScratch 클래스의 객체에 입력 데이터를 전달하면 해당 입력에 대한 예측값을 얻을 수 있습니다.
4.4.3. The Cross-Entropy Loss
Next we need to implement the cross-entropy loss function (introduced in Section 4.1.2). This may be the most common loss function in all of deep learning. At the moment, applications of deep learning easily cast classification problems far outnumber those better treated as regression problems.
4.1. Softmax Regression — Dive into Deep Learning 1.0.0-beta0 documentation
d2l.ai
다음으로 cross-entropy loss function-교차 엔트로피 손실 함수-를 구현해야 합니다(섹션 4.1.2에서 소개됨). 이것은 모든 딥 러닝에서 가장 일반적인 loss function-손실 함수-일 수 있습니다. 현재 딥 러닝의 응용 프로그램은 classification problems-분류 문제-를 쉽게 캐스팅하여 regression problems-회귀 문제-로 더 잘 처리되는 문제보다 훨씬 많습니다.
Recall that cross-entropy takes the negative log-likelihood of the predicted probability assigned to the true label. For efficiency we avoid Python for-loops and use indexing instead. In particular, the one-hot encoding in y allows us to select the matching terms in y^.
cross-entropy-교차 엔트로피-는 실제 레이블에 할당된 예측 확률의 negative log-likelihood-음의 로그 가능성-을 취한다는 점을 상기하십시오. 효율성을 위해 Python for-loops를 피하고 대신 인덱싱을 사용합니다. 특히 y의 one-hot encoding-원-핫 인코딩-을 사용하면 y^에서 일치하는 용어를 선택할 수 있습니다.
To see this in action we create sample data y_hat with 2 examples of predicted probabilities over 3 classes and their corresponding labels y. The correct labels are 0 and 2 respectively (i.e., the first and third class). Using y as the indices of the probabilities in y_hat, we can pick out terms efficiently.
이를 실제로 확인하기 위해 3개 클래스에 대한 predicted probabilities-예측 확률-의 2개 예와 해당 레이블 y로 샘플 데이터 y_hat을 만듭니다. 올바른 레이블은 각각 0과 2입니다(즉, 첫 번째 및 세 번째 클래스). y를 y_hat의 확률 지수로 사용하면 terms -용어-를 효율적으로 선택할 수 있습니다.
y = torch.tensor([0, 2])
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y_hat[[0, 1], y]이 코드는 y_hat 텐서에서 인덱스를 사용하여 특정 위치의 값을 선택하는 부분입니다. 코드를 한 줄씩 설명해드리겠습니다.
- y = torch.tensor([0, 2]): 정수로 이루어진 텐서 y를 생성합니다. y는 선택할 인덱스 값으로 사용됩니다.
- y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]]): y_hat 텐서를 생성합니다. y_hat은 예측값으로 이루어진 2차원 텐서입니다.
- y_hat[[0, 1], y]: y_hat 텐서에서 [0, 1] 위치의 행과 y 텐서의 값에 해당하는 열의 값들을 선택합니다. 즉, 첫 번째 행의 y[0] 값에 해당하는 열의 값과 두 번째 행의 y[1] 값에 해당하는 열의 값을 선택합니다.
결과적으로, y_hat[[0, 1], y]는 y_hat 텐서에서 첫 번째 행의 0번 열의 값과 두 번째 행의 2번 열의 값을 선택하여 반환합니다.

Now we can implement the cross-entropy loss function by averaging over the logarithms of the selected probabilities.
이제 선택한 probabilities-확률-의 logarithms -로그-를 평균화하여 cross-entropy loss function-교차 엔트로피 손실 함수-를 구현할 수 있습니다.
def cross_entropy(y_hat, y):
return -torch.log(y_hat[list(range(len(y_hat))), y]).mean()
cross_entropy(y_hat, y)
이 코드는 크로스 엔트로피 손실 함수를 계산하는 부분입니다. 코드를 한 줄씩 설명해드리겠습니다.
- def cross_entropy(y_hat, y): cross_entropy라는 함수를 정의합니다. 이 함수는 y_hat과 y를 입력으로 받습니다. y_hat은 예측값, y는 실제 레이블로 구성된 텐서입니다.
- -torch.log(y_hat[list(range(len(y_hat))), y]): y_hat 텐서의 예측값들 중에서 실제 레이블 y에 해당하는 위치의 로그값을 계산합니다. list(range(len(y_hat)))는 0부터 y_hat의 길이까지의 숫자 리스트를 생성하며, 이는 행 인덱스를 나타냅니다. y는 열 인덱스로 사용됩니다. 따라서 y_hat[list(range(len(y_hat))), y]는 y_hat에서 실제 레이블에 해당하는 위치의 값을 선택합니다.
- .mean(): 선택된 값들의 평균을 계산합니다.
결과적으로, cross_entropy(y_hat, y)는 예측값 y_hat과 실제 레이블 y를 이용하여 크로스 엔트로피 손실을 계산한 결과를 반환합니다.
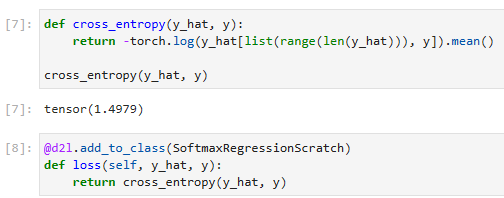
@d2l.add_to_class(SoftmaxRegressionScratch)
def loss(self, y_hat, y):
return cross_entropy(y_hat, y)위의 코드는 SoftmaxRegressionScratch 클래스에 loss 메서드를 추가하는 부분입니다. 코드를 한 줄씩 설명해드리겠습니다.
- @d2l.add_to_class(SoftmaxRegressionScratch): d2l 모듈의 add_to_class 데코레이터를 사용하여 SoftmaxRegressionScratch 클래스에 메서드를 추가합니다.
- def loss(self, y_hat, y): loss라는 메서드를 정의합니다. 이 메서드는 y_hat과 y를 입력으로 받습니다. y_hat은 예측값, y는 실제 레이블로 구성된 텐서입니다.
- return cross_entropy(y_hat, y): cross_entropy 함수를 호출하여 y_hat과 y를 이용하여 크로스 엔트로피 손실을 계산한 결과를 반환합니다.
결과적으로, loss 메서드는 SoftmaxRegressionScratch 클래스의 예측값 y_hat과 실제 레이블 y를 이용하여 크로스 엔트로피 손실을 계산한 결과를 반환합니다. 이렇게 추가된 loss 메서드는 모델의 학습 및 평가 과정에서 사용될 수 있습니다.
4.4.4. Training
We reuse the fit method defined in Section 3.4 to train the model with 10 epochs. Note that both the number of epochs (max_epochs), the minibatch size (batch_size), and learning rate (lr) are adjustable hyperparameters. That means that while these values are not learned during our primary training loop, they still influence the performance of our model, bot vis-a-vis training and generalization performance. In practice you will want to choose these values based on the validation split of the data and then to ultimately evaluate your final model on the test split. As discussed in Section 3.6.3, we will treat the test data of Fashion-MNIST as the validation set, thus reporting validation loss and validation accuracy on this split.
3.6. Generalization — Dive into Deep Learning 1.0.0-beta0 documentation
d2l.ai
섹션 3.4에서 정의한 fit method-적합 방법-을 재사용하여 10 epoch로 모델을 훈련합니다. Epoch 수(max_epochs), minibatch 크기(batch_size) 및 학습률(lr)은 모두 조정 가능한 hyperparameters-하이퍼파라미터-입니다. 즉, 이러한 값은 기본 교육 루프 중에 학습되지 않지만 여전히 모델의 성능, bot vis-a-vis training-봇 대비 교육- 및 generalization performance-일반화 성능-에 영향을 미칩니다. 실제로는 데이터의 validation split-검증 분할-을 기반으로 이러한 값을 선택한 다음 궁극적으로 test split-테스트 분할-에서 최종 모델을 평가하기를 원할 것입니다. 섹션 3.6.3에서 설명한 것처럼 Fashion-MNIST의 테스트 데이터를 validation set-유효성 검사 세트-로 취급하여 이 분할에서 validation loss -유효성 검사 손실- 및 validation accuracy on this split-유효성 검사 정확도-를 보고합니다.
data = d2l.FashionMNIST(batch_size=256)
model = SoftmaxRegressionScratch(num_inputs=784, num_outputs=10, lr=0.1)
trainer = d2l.Trainer(max_epochs=10)
trainer.fit(model, data)위의 코드는 FashionMNIST 데이터셋을 사용하여 Softmax 회귀 모델을 학습하는 과정을 보여줍니다. 코드를 한 줄씩 설명해드리겠습니다.
- data = d2l.FashionMNIST(batch_size=256): d2l 모듈의 FashionMNIST 클래스를 사용하여 FashionMNIST 데이터셋을 생성합니다. 배치 크기는 256로 설정되었습니다.
- model = SoftmaxRegressionScratch(num_inputs=784, num_outputs=10, lr=0.1): SoftmaxRegressionScratch 클래스의 인스턴스인 model을 생성합니다. 입력 특성 수는 784이고 출력 클래스 수는 10입니다. 학습률은 0.1로 설정되었습니다.
- trainer = d2l.Trainer(max_epochs=10): d2l 모듈의 Trainer 클래스를 사용하여 훈련을 관리하는 trainer 객체를 생성합니다. 최대 에포크 수는 10으로 설정되었습니다.
- trainer.fit(model, data): trainer 객체의 fit 메서드를 호출하여 모델 model과 데이터셋 data를 이용하여 모델을 학습시킵니다.
결과적으로, 위의 코드는 FashionMNIST 데이터셋을 사용하여 Softmax 회귀 모델을 10 에포크 동안 학습하는 과정을 보여줍니다. Trainer 클래스를 사용하여 모델의 학습을 관리하며, 학습된 모델은 model 객체에 저장됩니다.
Local에서 돌린 결과

CoLab에서 돌린 결과

4.4.5. Prediction
Now that training is complete, our model is ready to classify some images.
이제 교육이 완료되었으므로 모델은 일부 이미지를 분류할 준비가 되었습니다.
X, y = next(iter(data.val_dataloader()))
preds = model(X).argmax(axis=1)
preds.shape위의 코드는 검증 데이터셋에서 첫 번째 배치를 가져와서 모델에 입력으로 전달하고, 모델의 예측 결과를 저장하는 과정을 나타냅니다. 코드를 한 줄씩 설명해드리겠습니다.
- X, y = next(iter(data.val_dataloader())): data.val_dataloader()를 통해 검증 데이터셋의 첫 번째 배치를 가져옵니다. next(iter(...))를 사용하여 이터레이터에서 다음 값을 가져옵니다. X는 입력 데이터를, y는 해당 데이터의 정답 레이블을 나타냅니다.
- preds = model(X).argmax(axis=1): 모델 model에 입력 데이터 X를 전달하여 예측 결과를 얻습니다. model(X)는 입력 데이터에 대한 예측값을 반환합니다. argmax(axis=1)를 사용하여 각 데이터 포인트마다 가장 큰 값의 인덱스를 구합니다. 따라서 preds에는 각 데이터 포인트의 예측된 클래스 인덱스가 저장됩니다.
- preds.shape: preds의 형태(shape)를 확인합니다. 이는 예측된 클래스 인덱스의 개수를 나타냅니다.
결과적으로, 위의 코드는 검증 데이터셋에서 첫 번째 배치를 사용하여 모델의 예측 결과를 얻고, 예측된 클래스 인덱스를 preds에 저장합니다. preds의 형태(shape)를 확인하여 예측된 클래스 인덱스의 개수를 알 수 있습니다.
Local에서 돌린 결과

CoLab에서 돌린 결과

We are more interested in the images we label incorrectly. We visualize them by comparing their actual labels (first line of text output) with the predictions from the model (second line of text output).
우리는 잘못 라벨을 붙인 이미지에 더 관심이 있습니다. 실제 레이블(텍스트 출력의 첫 번째 줄)과 모델의 예측(텍스트 출력의 두 번째 줄)을 비교하여 시각화합니다.
wrong = preds.type(y.dtype) != y
X, y, preds = X[wrong], y[wrong], preds[wrong]
labels = [a+'\n'+b for a, b in zip(
data.text_labels(y), data.text_labels(preds))]
data.visualize([X, y], labels=labels)위의 코드는 잘못 예측된 샘플들을 시각화하는 과정을 나타냅니다. 코드를 한 줄씩 설명해드리겠습니다.
- wrong = preds.type(y.dtype) != y: 모델의 예측값 preds와 정답 레이블 y를 비교하여 잘못 예측된 샘플을 식별합니다. preds.type(y.dtype)를 사용하여 preds의 데이터 타입을 y와 일치시키고, != 연산자를 사용하여 예측값과 정답 레이블을 비교합니다. 이 결과를 wrong에 저장합니다.
- X, y, preds = X[wrong], y[wrong], preds[wrong]: 잘못 예측된 샘플에 대한 입력 데이터 X, 정답 레이블 y, 예측값 preds를 추출하여 각각 X[wrong], y[wrong], preds[wrong]에 저장합니다. 이렇게 하면 잘못 예측된 샘플들만 남게 됩니다.
- labels = [a+'\n'+b for a, b in zip(data.text_labels(y), data.text_labels(preds))]: 잘못 예측된 샘플들에 대한 정답 레이블 y와 예측값 preds를 사용하여 레이블 텍스트를 생성합니다. data.text_labels(y)와 data.text_labels(preds)를 순회하면서 정답 레이블과 예측값을 합쳐서 하나의 문자열로 만들고, 이를 labels 리스트에 저장합니다.
- data.visualize([X, y], labels=labels): 입력 데이터 X와 정답 레이블 y를 사용하여 시각화를 수행합니다. labels를 추가적인 인자로 전달하여 각 샘플의 레이블을 텍스트로 표시합니다.
결과적으로, 위의 코드는 잘못 예측된 샘플들을 추출하고, 해당 샘플들의 입력 데이터와 레이블을 시각화하여 표시합니다. 또한, 정답 레이블과 예측값을 텍스트로 표시하여 시각화에 추가합니다.
Local에서 돌린 결과
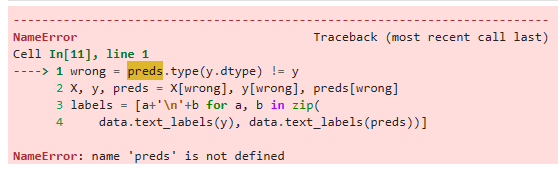
CoLab에서 돌린 결과

4.4.6. Summary
By now we are starting to get some experience with solving linear regression and classification problems. With it, we have reached what would arguably be the state of the art of 1960-1970s of statistical modeling. In the next section, we will show you how to leverage deep learning frameworks to implement this model much more efficiently.
이제 우리는 선형 회귀 및 분류 문제를 해결하는 경험을 쌓기 시작했습니다. 이를 통해 우리는 1960-1970년대의 통계 모델링 기술 수준에 도달했습니다. 다음 섹션에서는 딥 러닝 프레임워크를 활용하여 이 모델을 훨씬 더 효율적으로 구현하는 방법을 보여줍니다.
4.4.7. Exercises

'Dive into Deep Learning > D2L Linear Neural Networks' 카테고리의 다른 글
| D2L - 3.7. Weight Decay (1) | 2023.12.03 |
|---|---|
| D2L - 3.6. Generalization (1) | 2023.12.03 |
| D2L - 4.7. Environment and Distribution Shift (0) | 2023.06.27 |
| D2L - 4.6. Generalization in Classification (0) | 2023.06.27 |
| D2L - 4.5. Concise Implementation of Softmax Regression¶ (0) | 2023.06.27 |
| D2L - 4.3. The Base Classification Model (0) | 2023.06.26 |
| D2L - 4.2. The Image Classification Dataset (0) | 2023.06.26 |
| D2L 4.1. Softmax Regression (1) | 2023.06.26 |
| D2L - 4. Linear Neural Networks for Classification (0) | 2023.06.26 |
| D2L - Local Environment Setting (0) | 2023.06.26 |

