https://d2l.ai/chapter_linear-regression/weight-decay.html
3.7. Weight Decay — Dive into Deep Learning 1.0.3 documentation
d2l.ai
3.7. Weight Decay
Now that we have characterized the problem of overfitting, we can introduce our first regularization technique. Recall that we can always mitigate overfitting by collecting more training data. However, that can be costly, time consuming, or entirely out of our control, making it impossible in the short run. For now, we can assume that we already have as much high-quality data as our resources permit and focus the tools at our disposal when the dataset is taken as a given.
이제 과적합 문제를 특성화했으므로 첫 번째 정규화 기술을 소개할 수 있습니다. 더 많은 훈련 데이터를 수집하면 항상 과적합을 완화할 수 있다는 점을 기억하세요. 그러나 이는 비용이 많이 들고, 시간이 많이 걸리거나 완전히 통제할 수 없어 단기적으로 불가능할 수 있습니다. 지금은 리소스가 허용하는 만큼의 고품질 데이터를 이미 보유하고 있다고 가정하고 데이터 세트를 주어진 것으로 간주할 때 사용할 수 있는 도구에 집중할 수 있습니다.
Recall that in our polynomial regression example (Section 3.6.2.1) we could limit our model’s capacity by tweaking the degree of the fitted polynomial. Indeed, limiting the number of features is a popular technique for mitigating overfitting. However, simply tossing aside features can be too blunt an instrument. Sticking with the polynomial regression example, consider what might happen with high-dimensional input. The natural extensions of polynomials to multivariate data are called monomials, which are simply products of powers of variables. The degree of a monomial is the sum of the powers. For example, x1**2x2, and x3x5**2 (

)are both monomials of degree 3.
다항식 회귀 예제(섹션 3.6.2.1)에서 피팅된 다항식의 차수를 조정하여 모델의 용량을 제한할 수 있다는 점을 기억하세요. 실제로 특성 수를 제한하는 것은 과적합을 완화하는 데 널리 사용되는 기술입니다. 그러나 단순히 기능을 제쳐두는 것은 너무 무뚝뚝한 도구가 될 수 있습니다. 다항식 회귀 예제를 계속 사용하면서 고차원 입력에서 어떤 일이 발생할 수 있는지 생각해 보세요. 다변량 데이터에 대한 다항식의 자연스러운 확장을 단항식이라고 하며 이는 단순히 변수 거듭제곱의 곱입니다. 단항식의 차수는 거듭제곱의 합입니다. 예를 들어 x1**2x2와 x3x5**2 ()는 모두 3차 단항식입니다.
Note that the number of terms with degree d blows up rapidly as d grows larger. Given k variables, the number of monomials of degree d is (k−1+d k−1) (
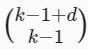
). Even small changes in degree, say from 2 to 3, dramatically increase the complexity of our model. Thus we often need a more fine-grained tool for adjusting function complexity.
d가 커짐에 따라 차수 d를 갖는 항의 수가 급격히 증가한다는 점에 유의하십시오. k개의 변수가 주어지면 d차 단항식의 수는 (k−1+d k−1)입니다. 2에서 3까지의 작은 변화조차도 모델의 복잡성을 극적으로 증가시킵니다. 따라서 함수 복잡성을 조정하기 위해 보다 세분화된 도구가 필요한 경우가 많습니다.
%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l
3.7.1. Norms and Weight Decay
Rather than directly manipulating the number of parameters, weight decay, operates by restricting the values that the parameters can take. More commonly called ℓ2 regularization outside of deep learning circles when optimized by minibatch stochastic gradient descent, weight decay might be the most widely used technique for regularizing parametric machine learning models. The technique is motivated by the basic intuition that among all functions f, the function f=0 (assigning the value 0 to all inputs) is in some sense the simplest, and that we can measure the complexity of a function by the distance of its parameters from zero. But how precisely should we measure the distance between a function and zero? There is no single right answer. In fact, entire branches of mathematics, including parts of functional analysis and the theory of Banach spaces, are devoted to addressing such issues.
매개변수 수를 직접 조작하는 대신 가중치 감소는 매개변수가 취할 수 있는 값을 제한하여 작동합니다. 미니배치 확률적 경사 하강법으로 최적화할 때 딥 러닝 분야 외부에서 더 일반적으로 ℓ2 정규화라고 불리는 가중치 감소는 파라메트릭 기계 학습 모델을 정규화하는 데 가장 널리 사용되는 기술일 수 있습니다. 이 기술은 모든 함수 f 중에서 함수 f=0(모든 입력에 값 0을 할당하는)이 어떤 의미에서는 가장 단순하며 함수의 복잡성을 함수의 거리로 측정할 수 있다는 기본적인 직관에 의해 동기가 부여되었습니다. 매개변수는 0부터 시작됩니다. 하지만 함수와 0 사이의 거리를 얼마나 정확하게 측정해야 할까요? 정답은 하나도 없습니다. 실제로 기능 분석의 일부와 바나흐 공간 이론을 포함한 수학의 전체 분야가 이러한 문제를 해결하는 데 전념하고 있습니다.
One simple interpretation might be to measure the complexity of a linear function f(x)=w⊤x by some norm of its weight vector, e.g., ‖w‖**2. Recall that we introduced the ℓ2 norm and ℓ1 norm, which are special cases of the more general ℓp norm, in Section 2.3.11. The most common method for ensuring a small weight vector is to add its norm as a penalty term to the problem of minimizing the loss. Thus we replace our original objective, minimizing the prediction loss on the training labels, with new objective, minimizing the sum of the prediction loss and the penalty term. Now, if our weight vector grows too large, our learning algorithm might focus on minimizing the weight norm ‖w‖**2 rather than minimizing the training error. That is exactly what we want. To illustrate things in code, we revive our previous example from Section 3.1 for linear regression. There, our loss was given by
한 가지 간단한 해석은 선형 함수 f(x)=w⊤x의 복잡성을 해당 가중치 벡터의 일부 표준(예: "w"**2)으로 측정하는 것입니다. 섹션 2.3.11에서 보다 일반적인 ℓp 노름의 특수한 경우인 ℓ2 노름과 ℓ1 노름을 소개했음을 기억하세요. 작은 가중치 벡터를 보장하는 가장 일반적인 방법은 손실을 최소화하는 문제에 페널티 항으로 해당 노름을 추가하는 것입니다. 따라서 우리는 훈련 라벨의 예측 손실을 최소화하는 원래 목표를 예측 손실과 페널티 항의 합을 최소화하는 새로운 목표로 대체합니다. 이제 가중치 벡터가 너무 커지면 학습 알고리즘은 훈련 오류를 최소화하는 대신 가중치 표준 "w"**2를 최소화하는 데 중점을 둘 수 있습니다. 그것이 바로 우리가 원하는 것입니다. 코드로 내용을 설명하기 위해 선형 회귀에 대한 섹션 3.1의 이전 예제를 되살립니다. 거기에서 우리의 손실은 다음과 같습니다.

Recall that x**(i) are the features, y**(i) is the label for any data example i, and (w,b) are the weight and bias parameters, respectively. To penalize the size of the weight vector, we must somehow add ‖w‖**2 to the loss function, but how should the model trade off the standard loss for this new additive penalty? In practice, we characterize this trade-off via the regularization constant λ , a nonnegative hyperparameter that we fit using validation data:
x**(i)는 특징이고, y**(i)는 데이터 예제 i에 대한 레이블이며, (w,b)는 각각 가중치 및 편향 매개변수라는 점을 기억하세요. 가중치 벡터의 크기에 페널티를 적용하려면 어떻게든 손실 함수에 "w"**2를 추가해야 합니다. 하지만 모델은 이 새로운 추가 페널티에 대한 표준 손실을 어떻게 교환해야 할까요? 실제로 우리는 검증 데이터를 사용하여 피팅한 음이 아닌 하이퍼파라미터인 정규화 상수 λ를 통해 이러한 절충안을 특성화합니다.

For λ =0, we recover our original loss function. For λ >0, we restrict the size of ‖W‖. We divide by 2 by convention: when we take the derivative of a quadratic function, the 2 and 1/2 cancel out, ensuring that the expression for the update looks nice and simple. The astute reader might wonder why we work with the squared norm and not the standard norm (i.e., the Euclidean distance). We do this for computational convenience. By squaring the ℓ2 norm, we remove the square root, leaving the sum of squares of each component of the weight vector. This makes the derivative of the penalty easy to compute: the sum of derivatives equals the derivative of the sum.
λ =0인 경우 원래의 손실 함수를 복구합니다. λ >0인 경우 "W" 크기를 제한합니다. 관례에 따라 2로 나눕니다. 이차 함수의 미분을 취하면 2와 1/2이 상쇄되어 업데이트에 대한 식이 멋지고 단순해 보입니다. 기민한 독자라면 왜 우리가 표준 표준(예: 유클리드 거리)이 아닌 제곱 표준을 사용하여 작업하는지 궁금할 것입니다. 우리는 계산상의 편의를 위해 이렇게 합니다. ℓ2 노름을 제곱함으로써 제곱근을 제거하고 가중치 벡터의 각 구성요소의 제곱합을 남깁니다. 이는 페널티의 미분을 계산하기 쉽게 만듭니다. 미분의 합은 합계의 미분과 같습니다.
Moreover, you might ask why we work with the ℓ2 norm in the first place and not, say, the ℓ1 norm. In fact, other choices are valid and popular throughout statistics. While ℓ2-regularized linear models constitute the classic ridge regression algorithm, ℓ1-regularized linear regression is a similarly fundamental method in statistics, popularly known as lasso regression. One reason to work with the ℓ2 norm is that it places an outsize penalty on large components of the weight vector. This biases our learning algorithm towards models that distribute weight evenly across a larger number of features. In practice, this might make them more robust to measurement error in a single variable. By contrast, ℓ1 penalties lead to models that concentrate weights on a small set of features by clearing the other weights to zero. This gives us an effective method for feature selection, which may be desirable for other reasons. For example, if our model only relies on a few features, then we may not need to collect, store, or transmit data for the other (dropped) features.
게다가 왜 우리가 ℓ1 표준이 아닌 ℓ2 표준으로 작업하는지 궁금할 수도 있습니다. 실제로 통계 전반에 걸쳐 다른 선택이 유효하고 널리 사용됩니다. ℓ2 정규화 선형 모델이 고전적인 능선 회귀 알고리즘을 구성하는 반면, ℓ1 정규화 선형 회귀는 lasso 회귀로 널리 알려진 통계의 유사한 기본 방법입니다. ℓ2 표준을 사용하는 한 가지 이유는 가중치 벡터의 큰 구성요소에 특대 페널티를 적용한다는 것입니다. 이는 우리의 학습 알고리즘을 더 많은 수의 특성에 균등하게 가중치를 분배하는 모델로 편향시킵니다. 실제로 이는 단일 변수의 측정 오류에 더욱 강력해질 수 있습니다. 대조적으로, ℓ1 페널티는 다른 가중치를 0으로 지워서 작은 특성 집합에 가중치를 집중시키는 모델로 이어집니다. 이는 다른 이유로 바람직할 수 있는 특징 선택을 위한 효과적인 방법을 제공합니다. 예를 들어 모델이 몇 가지 기능에만 의존하는 경우 다른(삭제된) 기능에 대한 데이터를 수집, 저장 또는 전송할 필요가 없을 수 있습니다.
Using the same notation in (3.1.11), minibatch stochastic gradient descent updates for ℓ2-regularized regression as follows:
(3.1.11)의 동일한 표기법을 사용하여 ℓ2 정규 회귀에 대한 미니배치 확률적 경사하강법 업데이트는 다음과 같습니다.
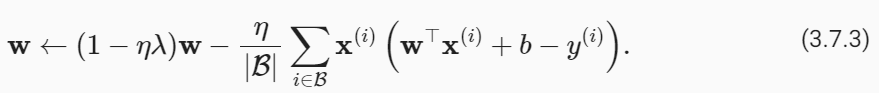
As before, we update w based on the amount by which our estimate differs from the observation. However, we also shrink the size of w towards zero. That is why the method is sometimes called “weight decay”: given the penalty term alone, our optimization algorithm decays the weight at each step of training. In contrast to feature selection, weight decay offers us a mechanism for continuously adjusting the complexity of a function. Smaller values of λ correspond to less constrained w, whereas larger values of λ constrain w more considerably. Whether we include a corresponding bias penalty b**2 can vary across implementations, and may vary across layers of a neural network. Often, we do not regularize the bias term. Besides, although ℓ2 regularization may not be equivalent to weight decay for other optimization algorithms, the idea of regularization through shrinking the size of weights still holds true.
이전과 마찬가지로 추정값이 관측값과 다른 정도에 따라 w를 업데이트합니다. 그러나 w의 크기도 0으로 축소합니다. 이것이 바로 이 방법을 "가중치 감소"라고 부르는 이유입니다. 페널티 항만 주어지면 우리의 최적화 알고리즘은 훈련의 각 단계에서 가중치를 감소시킵니다. 기능 선택과 달리 가중치 감소는 기능의 복잡성을 지속적으로 조정하는 메커니즘을 제공합니다. λ의 값이 작을수록 w가 덜 제한되는 반면, λ의 값이 클수록 w가 더 크게 제한됩니다. 해당 바이어스 페널티 b**2를 포함하는지 여부는 구현에 따라 다를 수 있으며 신경망의 계층에 따라 다를 수 있습니다. 종종 우리는 편향 항을 정규화하지 않습니다. 게다가 ℓ2 정규화는 다른 최적화 알고리즘의 가중치 감소와 동일하지 않을 수 있지만 가중치 크기 축소를 통한 정규화 아이디어는 여전히 유효합니다.
3.7.2. High-Dimensional Linear Regression
We can illustrate the benefits of weight decay through a simple synthetic example.
간단한 합성 예를 통해 체중 감소의 이점을 설명할 수 있습니다.
First, we generate some data as before:
먼저 이전과 같이 일부 데이터를 생성합니다.
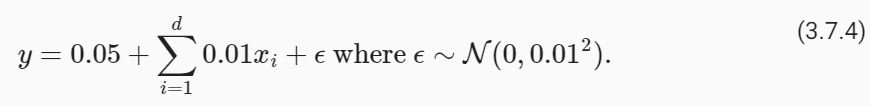
In this synthetic dataset, our label is given by an underlying linear function of our inputs, corrupted by Gaussian noise with zero mean and standard deviation 0.01. For illustrative purposes, we can make the effects of overfitting pronounced, by increasing the dimensionality of our problem to d=200 and working with a small training set with only 20 examples.
이 합성 데이터 세트에서 레이블은 평균이 0이고 표준 편차가 0.01인 가우스 노이즈로 인해 손상된 입력의 기본 선형 함수로 제공됩니다. 설명을 위해 문제의 차원을 d=200으로 늘리고 20개의 예제만 있는 작은 훈련 세트로 작업하여 과적합의 효과를 뚜렷하게 만들 수 있습니다.
class Data(d2l.DataModule):
def __init__(self, num_train, num_val, num_inputs, batch_size):
self.save_hyperparameters()
n = num_train + num_val
self.X = torch.randn(n, num_inputs)
noise = torch.randn(n, 1) * 0.01
w, b = torch.ones((num_inputs, 1)) * 0.01, 0.05
self.y = torch.matmul(self.X, w) + b + noise
def get_dataloader(self, train):
i = slice(0, self.num_train) if train else slice(self.num_train, None)
return self.get_tensorloader([self.X, self.y], train, i)
3.7.3. Implementation from Scratc
Now, let’s try implementing weight decay from scratch. Since minibatch stochastic gradient descent is our optimizer, we just need to add the squared ℓ2 penalty to the original loss function.
이제 처음부터 가중치 감소를 구현해 보겠습니다. 미니배치 확률적 경사하강법이 우리의 최적화 프로그램이므로 원래 손실 함수에 제곱된 ℓ2 페널티를 추가하기만 하면 됩니다.
3.7.3.1. Defining ℓ2 Norm Penalty
Perhaps the most convenient way of implementing this penalty is to square all terms in place and sum them.
아마도 이 페널티를 구현하는 가장 편리한 방법은 모든 항을 제곱하고 합하는 것입니다.
def l2_penalty(w):
return (w ** 2).sum() / 2
3.7.3.2. Defining the Model
In the final model, the linear regression and the squared loss have not changed since Section 3.4, so we will just define a subclass of d2l.LinearRegressionScratch. The only change here is that our loss now includes the penalty term.
최종 모델에서는 선형 회귀와 제곱 손실이 섹션 3.4 이후로 변경되지 않았으므로 d2l.LinearRegressionScratch의 하위 클래스만 정의하겠습니다. 여기서 유일한 변경 사항은 이제 손실에 페널티 기간이 포함된다는 것입니다.
class WeightDecayScratch(d2l.LinearRegressionScratch):
def __init__(self, num_inputs, lambd, lr, sigma=0.01):
super().__init__(num_inputs, lr, sigma)
self.save_hyperparameters()
def loss(self, y_hat, y):
return (super().loss(y_hat, y) +
self.lambd * l2_penalty(self.w))
The following code fits our model on the training set with 20 examples and evaluates it on the validation set with 100 examples.
다음 코드는 20개의 예제가 있는 훈련 세트에 모델을 맞추고 100개의 예제가 있는 검증 세트에서 모델을 평가합니다.
data = Data(num_train=20, num_val=100, num_inputs=200, batch_size=5)
trainer = d2l.Trainer(max_epochs=10)
def train_scratch(lambd):
model = WeightDecayScratch(num_inputs=200, lambd=lambd, lr=0.01)
model.board.yscale='log'
trainer.fit(model, data)
print('L2 norm of w:', float(l2_penalty(model.w)))
3.7.3.3. Training without Regularization
We now run this code with lambd = 0, disabling weight decay. Note that we overfit badly, decreasing the training error but not the validation error—a textbook case of overfitting.
이제 이 코드를 Lambd = 0으로 실행하여 가중치 감소를 비활성화합니다. 우리는 과적합을 심하게 하여 학습 오류를 줄였지만 검증 오류는 줄이지 않았습니다. 이는 과적합의 교과서적인 사례입니다.
train_scratch(0)
L2 norm of w: 0.009948714636266232

3.7.3.4. Using Weight Decay
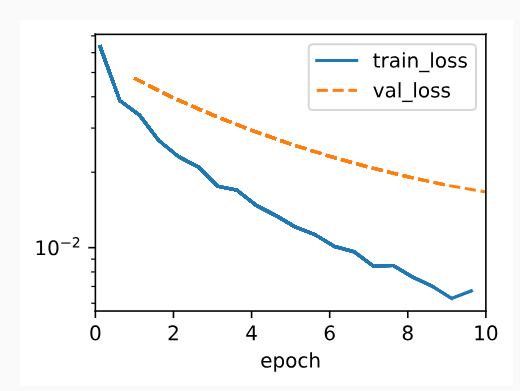
Below, we run with substantial weight decay. Note that the training error increases but the validation error decreases. This is precisely the effect we expect from regularization.
아래에서는 상당한 체중 감소를 보여줍니다. 학습 오류는 증가하지만 검증 오류는 감소합니다. 이것이 바로 우리가 정규화에서 기대하는 효과입니다.
train_scratch(3)L2 norm of w: 0.0017270983662456274
3.7.4. Concise Implementation
Because weight decay is ubiquitous in neural network optimization, the deep learning framework makes it especially convenient, integrating weight decay into the optimization algorithm itself for easy use in combination with any loss function. Moreover, this integration serves a computational benefit, allowing implementation tricks to add weight decay to the algorithm, without any additional computational overhead. Since the weight decay portion of the update depends only on the current value of each parameter, the optimizer must touch each parameter once anyway.
가중치 감소는 신경망 최적화에서 어디에나 존재하기 때문에 딥 러닝 프레임워크는 모든 손실 함수와 결합하여 쉽게 사용할 수 있도록 최적화 알고리즘 자체에 가중치 감소를 통합하여 이를 특히 편리하게 만듭니다. 또한 이러한 통합은 추가 계산 오버헤드 없이 알고리즘에 가중치 감소를 추가하는 구현 트릭을 허용하므로 계산상의 이점을 제공합니다. 업데이트의 가중치 감소 부분은 각 매개변수의 현재 값에만 의존하므로 최적화 프로그램은 어쨌든 각 매개변수를 한 번 터치해야 합니다.
Below, we specify the weight decay hyperparameter directly through weight_decay when instantiating our optimizer. By default, PyTorch decays both weights and biases simultaneously, but we can configure the optimizer to handle different parameters according to different policies. Here, we only set weight_decay for the weights (the net.weight parameters), hence the bias (the net.bias parameter) will not decay.
아래에서는 최적화 프로그램을 인스턴스화할 때 Weight_decay를 통해 직접 가중치 감소 하이퍼파라미터를 지정합니다. 기본적으로 PyTorch는 가중치와 편향을 동시에 감소시키지만, 다양한 정책에 따라 다양한 매개변수를 처리하도록 최적화 프로그램을 구성할 수 있습니다. 여기서는 가중치(net.weight 매개변수)에 대해서만 Weight_decay를 설정하므로 편향(net.bias 매개변수)은 감소하지 않습니다.
class WeightDecay(d2l.LinearRegression):
def __init__(self, wd, lr):
super().__init__(lr)
self.save_hyperparameters()
self.wd = wd
def configure_optimizers(self):
return torch.optim.SGD([
{'params': self.net.weight, 'weight_decay': self.wd},
{'params': self.net.bias}], lr=self.lr)
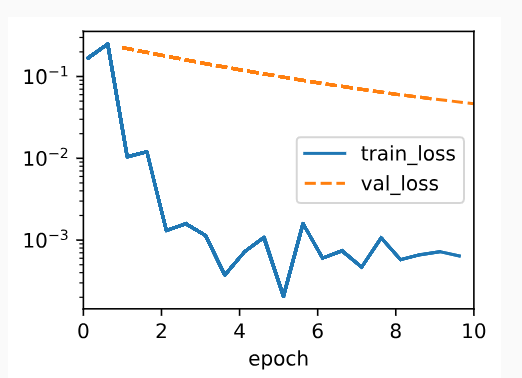
The plot looks similar to that when we implemented weight decay from scratch. However, this version runs faster and is easier to implement, benefits that will become more pronounced as you address larger problems and this work becomes more routine.
플롯은 처음부터 가중치 감소를 구현했을 때와 유사해 보입니다. 그러나 이 버전은 더 빠르게 실행되고 구현하기가 더 쉬우므로 더 큰 문제를 해결하고 이 작업이 더 일상화될수록 이점이 더욱 뚜렷해집니다.
model = WeightDecay(wd=3, lr=0.01)
model.board.yscale='log'
trainer.fit(model, data)
print('L2 norm of w:', float(l2_penalty(model.get_w_b()[0])))
L2 norm of w: 0.013779522851109505
So far, we have touched upon one notion of what constitutes a simple linear function. However, even for simple nonlinear functions, the situation can be much more complex. To see this, the concept of reproducing kernel Hilbert space (RKHS) allows one to apply tools introduced for linear functions in a nonlinear context. Unfortunately, RKHS-based algorithms tend to scale poorly to large, high-dimensional data. In this book we will often adopt the common heuristic whereby weight decay is applied to all layers of a deep network.
지금까지 우리는 단순한 선형 함수를 구성하는 개념 중 하나를 다루었습니다. 그러나 단순한 비선형 함수의 경우에도 상황은 훨씬 더 복잡할 수 있습니다. 이를 확인하기 위해 RKHS(커널 힐베르트 공간 재현) 개념을 사용하면 비선형 맥락에서 선형 함수에 대해 도입된 도구를 적용할 수 있습니다. 불행하게도 RKHS 기반 알고리즘은 대규모 고차원 데이터에 제대로 확장되지 않는 경향이 있습니다. 이 책에서 우리는 딥 네트워크의 모든 계층에 가중치 감소를 적용하는 일반적인 경험적 방법을 자주 채택할 것입니다.
3.7.5. Summary
Regularization is a common method for dealing with overfitting. Classical regularization techniques add a penalty term to the loss function (when training) to reduce the complexity of the learned model. One particular choice for keeping the model simple is using an ℓ2 penalty. This leads to weight decay in the update steps of the minibatch stochastic gradient descent algorithm. In practice, the weight decay functionality is provided in optimizers from deep learning frameworks. Different sets of parameters can have different update behaviors within the same training loop.
정규화는 과적합을 처리하는 일반적인 방법입니다. 고전적인 정규화 기술은 학습된 모델의 복잡성을 줄이기 위해 (훈련 시) 손실 함수에 페널티 항을 추가합니다. 모델을 단순하게 유지하기 위한 한 가지 특별한 선택은 다음을 사용하는 것입니다.
패널티. 이로 인해 미니배치 확률적 경사하강법 알고리즘의 업데이트 단계에서 가중치 감소가 발생합니다. 실제로 가중치 감소 기능은 딥러닝 프레임워크의 최적화 프로그램에서 제공됩니다. 서로 다른 매개변수 세트는 동일한 훈련 루프 내에서 서로 다른 업데이트 동작을 가질 수 있습니다.
3.7.6. Exercises

'Dive into Deep Learning > D2L Linear Neural Networks' 카테고리의 다른 글
| D2L - 3.6. Generalization (1) | 2023.12.03 |
|---|---|
| D2L - 4.7. Environment and Distribution Shift (0) | 2023.06.27 |
| D2L - 4.6. Generalization in Classification (0) | 2023.06.27 |
| D2L - 4.5. Concise Implementation of Softmax Regression¶ (0) | 2023.06.27 |
| D2L - 4.4. Softmax Regression Implementation from Scratch (0) | 2023.06.26 |
| D2L - 4.3. The Base Classification Model (0) | 2023.06.26 |
| D2L - 4.2. The Image Classification Dataset (0) | 2023.06.26 |
| D2L 4.1. Softmax Regression (1) | 2023.06.26 |
| D2L - 4. Linear Neural Networks for Classification (0) | 2023.06.26 |
| D2L - Local Environment Setting (0) | 2023.06.26 |
