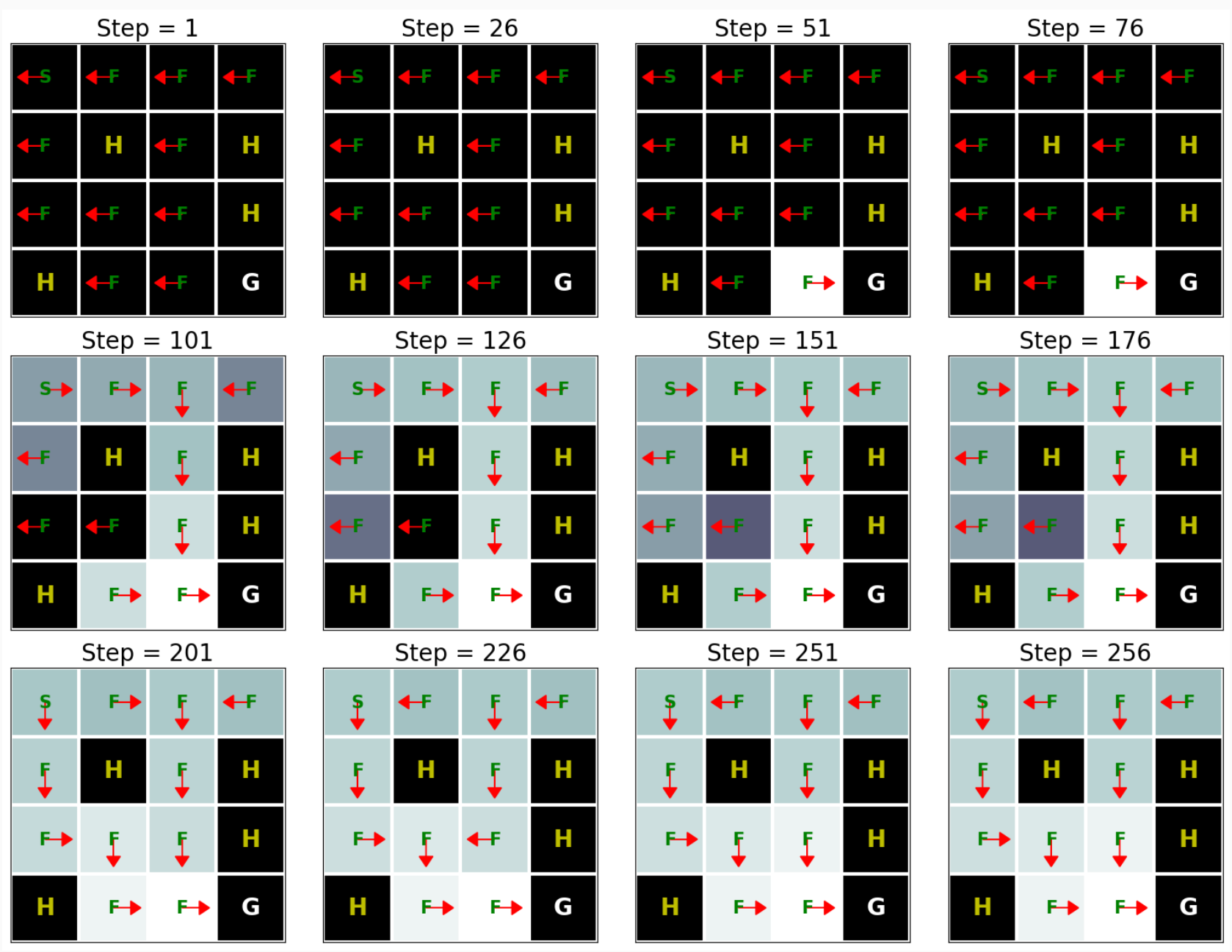
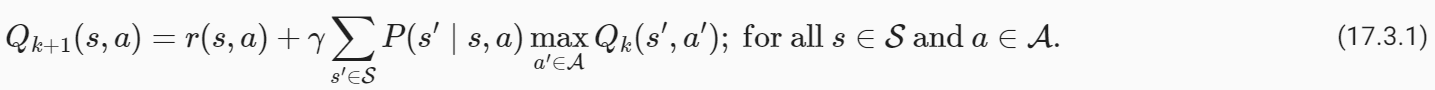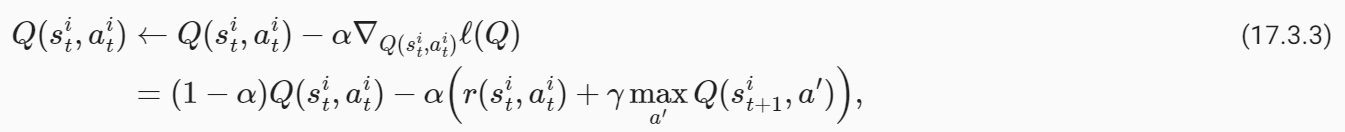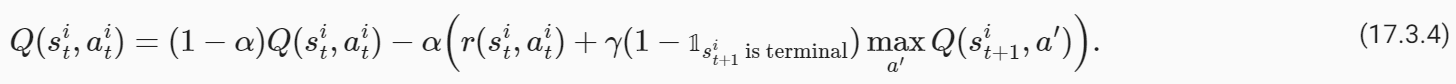18.1. Introduction to Gaussian Processes — Dive into Deep Learning 1.0.3 documentation (d2l.ai)

18.1. Introduction to Gaussian Processes

Let’s get a feel for how Gaussian processes operate, by starting with some examples.

몇 가지 예를 통해 가우스 프로세스가 어떻게 작동하는지 살펴보겠습니다.

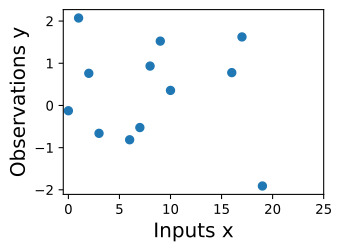
Suppose we observe the following dataset, of regression targets (outputs), y, indexed by inputs, x. As an example, the targets could be changes in carbon dioxide concentrations, and the inputs could be the times at which these targets have been recorded. What are some features of the data? How quickly does it seem to varying? Do we have data points collected at regular intervals, or are there missing inputs? How would you imagine filling in the missing regions, or forecasting up until x=25?

입력 x로 인덱싱된 회귀 목표(출력) y의 다음 데이터 세트를 관찰한다고 가정합니다. 예를 들어 목표는 이산화탄소 농도의 변화일 수 있고 입력은 이러한 목표가 기록된 시간일 수 있습니다. 데이터의 일부 기능은 무엇입니까? 얼마나 빨리 변하는 것 같나요? 정기적으로 수집된 데이터 포인트가 있습니까, 아니면 누락된 입력이 있습니까? 누락된 영역을 채우거나 x=25까지 예측하는 것을 어떻게 상상하시겠습니까?

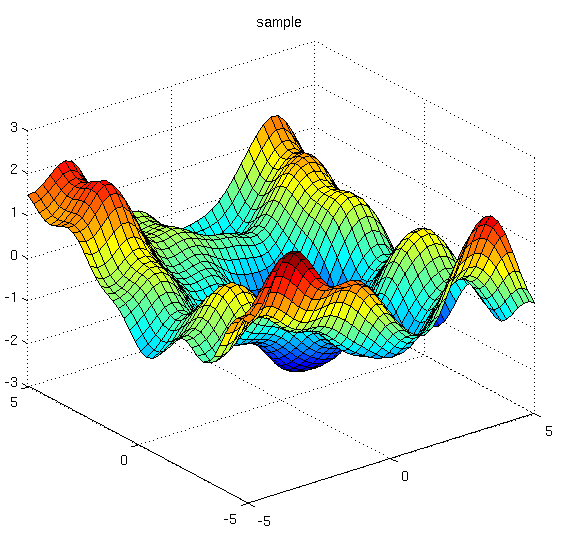
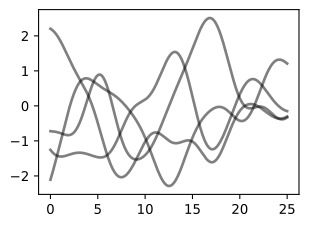
In order to fit the data with a Gaussian process, we start by specifying a prior distribution over what types of functions we might believe to be reasonable. Here we show several sample functions from a Gaussian process. Does this prior look reasonable? Note here we are not looking for functions that fit our dataset, but instead for specifying reasonable high-level properties of the solutions, such as how quickly they vary with inputs. Note that we will see code for reproducing all of the plots in this notebook, in the next notebooks on priors and inference.

데이터를 가우스 프로세스에 맞추려면 합리적이라고 믿을 수 있는 함수 유형에 대한 사전 분포를 지정하는 것부터 시작합니다. 여기서는 가우스 프로세스의 몇 가지 샘플 함수를 보여줍니다. 이 사전 조치가 합리적으로 보입니까? 여기서는 데이터 세트에 맞는 함수를 찾는 것이 아니라 입력에 따라 얼마나 빨리 변하는 지와 같은 솔루션의 합리적인 상위 수준 속성을 지정하기 위한 것입니다. 사전 및 추론에 대한 다음 노트북에서 이 노트북의 모든 플롯을 재현하기 위한 코드를 볼 수 있습니다.

Once we condition on data, we can use this prior to infer a posterior distribution over functions that could fit the data. Here we show sample posterior functions.

데이터에 조건을 적용하면 데이터에 적합한 함수에 대한 사후 분포를 추론하기 전에 이를 사용할 수 있습니다. 여기서는 샘플 사후 함수를 보여줍니다.

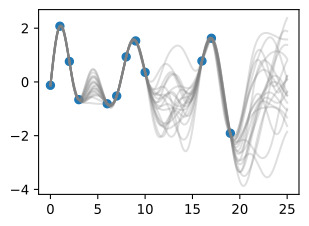
We see that each of these functions are entirely consistent with our data, perfectly running through each observation. In order to use these posterior samples to make predictions, we can average the values of every possible sample function from the posterior, to create the curve below, in thick blue. Note that we do not actually have to take an infinite number of samples to compute this expectation; as we will see later, we can compute the expectation in closed form.

우리는 이러한 각 함수가 데이터와 완전히 일치하며 각 관찰을 통해 완벽하게 실행된다는 것을 알 수 있습니다. 예측을 위해 이러한 사후 샘플을 사용하기 위해 사후에서 가능한 모든 샘플 함수의 값을 평균화하여 아래 곡선을 두꺼운 파란색으로 만들 수 있습니다. 이 기대치를 계산하기 위해 실제로 무한한 수의 샘플을 취할 필요는 없습니다. 나중에 살펴보겠지만 닫힌 형식으로 기대값을 계산할 수 있습니다.

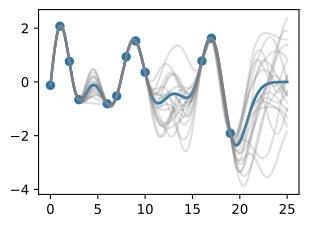
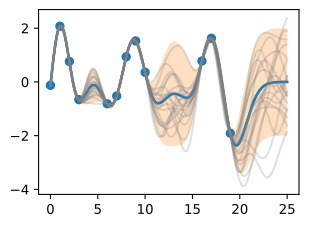
We may also want a representation of uncertainty, so we know how confident we should be in our predictions. Intuitively, we should have more uncertainty where there is more variability in the sample posterior functions, as this tells us there are many more possible values the true function could take. This type of uncertainty is called epistemic uncertainty, which is the reducible uncertainty associated with lack of information. As we acquire more data, this type of uncertainty disappears, as there will be increasingly fewer solutions consistent with what we observe. Like with the posterior mean, we can compute the posterior variance (the variability of these functions in the posterior) in closed form. With shade, we show two times the posterior standard deviation on either side of the mean, creating a credible interval that has a 95% probability of containing the true value of the function for any input x.

우리는 불확실성을 표현하기를 원할 수도 있으므로 예측에 얼마나 자신감을 가져야 하는지 알 수 있습니다. 직관적으로, 표본 사후 함수에 변동성이 더 많을수록 불확실성이 커집니다. 이는 실제 함수가 취할 수 있는 가능한 값이 더 많다는 것을 의미하기 때문입니다. 이러한 유형의 불확실성을 인식론적 불확실성이라고 하며, 이는 정보 부족과 관련된 환원 가능한 불확실성입니다. 더 많은 데이터를 수집할수록 우리가 관찰한 것과 일치하는 솔루션이 점점 줄어들기 때문에 이러한 유형의 불확실성은 사라집니다. 사후 평균과 마찬가지로 사후 분산(후방에서 이러한 함수의 변동성)을 닫힌 형식으로 계산할 수 있습니다. 음영을 사용하면 평균의 양쪽에 사후 표준 편차의 두 배를 표시하여 입력 x에 대한 함수의 실제 값을 포함할 확률이 95%인 신뢰할 수 있는 구간을 만듭니다.

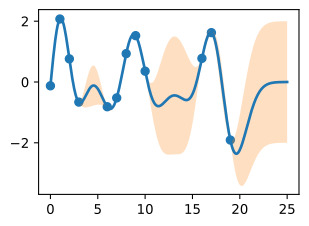
The plot looks somewhat cleaner if we remove the posterior samples, simply visualizing the data, posterior mean, and 95% credible set. Notice how the uncertainty grows away from the data, a property of epistemic uncertainty.

사후 샘플을 제거하고 데이터, 사후 평균 및 95% 신뢰 세트를 시각화하면 플롯이 다소 더 깨끗해 보입니다. 인식론적 불확실성의 속성인 불확실성이 데이터에서 어떻게 멀어지는지 주목하세요.

The properties of the Gaussian process that we used to fit the data are strongly controlled by what’s called a covariance function, also known as a kernel. The covariance function we used is called the RBF (Radial Basis Function) kernel, which has the form

데이터를 맞추는 데 사용한 가우스 프로세스의 속성은 커널이라고도 알려진 공분산 함수에 의해 강력하게 제어됩니다. 우리가 사용한 공분산 함수는 RBF(방사형 기초 함수) 커널이라고 하며 다음과 같은 형식을 갖습니다.

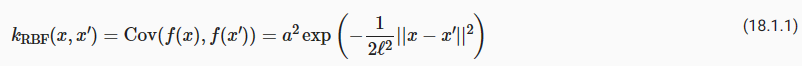
공분산 함수 (Covariance function) 란?

Covariance function (also known as a kernel function in machine learning) is a mathematical function used in statistics and machine learning to quantify the degree to which two random variables (or data points) vary together. It provides a measure of how correlated or related two variables are to each other.

공분산 함수 (머신 러닝에서는 커널 함수로도 알려져 있음)는 통계 및 머신 러닝에서 두 개의 랜덤 변수(또는 데이터 포인트)가 함께 얼마나 변하는지를 측정하는 수학적 함수입니다. 이것은 두 변수가 서로 어떻게 상관되거나 관련되어 있는지를 측정하는 데 사용됩니다.

In the context of statistics and Gaussian processes, the covariance function specifies the relationship between different points in a dataset. It defines how the value of one data point covaries or varies with the value of another data point. This information is crucial for modeling and understanding the underlying patterns and relationships within the data.

Covariance functions are often used in:

통계 및 가우시안 프로세스의 맥락에서 공분산 함수는 데이터 집합의 서로 다른 지점 간의 관계를 지정합니다. 이것은 하나의 데이터 포인트의 값이 다른 데이터 포인트의 값과 어떻게 공분산하거나 변하는지를 정의합니다. 이 정보는 데이터 내부의 기본적인 패턴과 관계를 모델링하고 이해하는 데 중요합니다.

공분산 함수는 다음과 같은 분야에서 사용됩니다.

1. Gaussian Processes: In Gaussian processes, the covariance function (kernel) is a fundamental component. It determines how the values of the function being modeled vary across different input points. Common covariance functions include the Radial Basis Function (RBF) kernel, Matérn kernel, and many others.
   
   가우시안 프로세스: 가우시안 프로세스에서 공분산 함수(커널)는 기본 구성 요소입니다. 이것은 모델링하려는 함수의 값이 다른 입력 지점에서 어떻게 변하는지를 결정합니다. 일반적인 공분산 함수에는 방사형 기저 함수(RBF) 커널, Matérn 커널 및 기타 여러 가지가 있습니다.
   
   
2. Spatial Statistics: In geostatistics and spatial statistics, covariance functions are used to model spatial dependencies in data, such as the correlation between temperatures at different locations on a map.
   
   공간 통계: 지오통계 및 공간 통계에서 공분산 함수는 데이터 내에서 공간적 종속성(지도상의 다른 위치에서 온도 간의 상관 관계와 같은)을 모델링하는 데 사용됩니다.
   
   
3. Machine Learning: In machine learning, covariance functions are used in various algorithms, especially in kernel methods, including Support Vector Machines (SVMs) and Gaussian Process Regression (GPR).
   
   머신 러닝: 머신 러닝에서 공분산 함수는 서포트 벡터 머신(SVM) 및 가우시안 프로세스 회귀(GPR)를 포함한 다양한 알고리즘에서 사용됩니다.
   
   

The choice of covariance function or kernel function has a significant impact on the performance of a model. Different covariance functions capture different types of relationships in the data, such as smoothness, periodicity, or linearity. Adjusting the parameters of the covariance function allows for fine-tuning the model's behavior.

공분산 함수 또는 커널 함수의 선택은 모델의 성능에 큰 영향을 미칩니다. 서로 다른 공분산 함수는 데이터에서 서로 다른 유형의 관계(부드러움, 주기성, 직선성 등)를 포착하며 공분산 함수의 매개변수를 조정하면 모델의 동작을 세밀하게 조정할 수 있습니다.

The hyperparameters of this kernel are interpretable. The amplitude parameter 'a' controls the vertical scale over which the function is varying, and the length-scale parameter ℓ controls the rate of variation (the wiggliness) of the function. Larger 'a' means larger function values, and larger ℓ means more slowly varying functions. Let’s see what happens to our sample prior and posterior functions as we vary 'a' and ℓ.

이 커널의 하이퍼파라미터는 해석 가능합니다. 진폭 매개변수 'a'는 함수가 변하는 수직 스케일을 제어하고, 길이 스케일 매개변수 ℓ는 함수의 변동률(흔들림)을 제어합니다. 'a'가 클수록 함수 값이 크고, ℓ가 클수록 함수가 천천히 변한다는 의미입니다. 'a'와 ℓ를 변경하면 샘플 사전 및 사후 함수에 어떤 일이 발생하는지 살펴보겠습니다.

The length-scale has a particularly pronounced effect on the predictions and uncertainty of a GP. At ||x−x′||=ℓ , the covariance between a pair of function values is a**2exp⁡(−0.5). At larger distances than ℓ , the values of the function values becomes nearly uncorrelated. This means that if we want to make a prediction at a point x∗, then function values with inputs x such that ||x−x′||>ℓ will not have a strong effect on our predictions.

길이 척도는 GP의 예측과 불확실성에 특히 뚜렷한 영향을 미칩니다. ||x−x′||=ℓ 에서 함수 값 쌍 사이의 공분산은 a**2exp⁡(−0.5)입니다. ℓ 보다 큰 거리에서는 함수 값의 상관관계가 거의 없어집니다. 이는 x* 지점에서 예측을 수행하려는 경우 ||x−x′||>ℓ와 같은 입력 x가 있는 함수 값이 예측에 큰 영향을 미치지 않음을 의미합니다.

Let’s see how changing the lengthscale affects sample prior and posterior functions, and credible sets. The above fits use a length-scale of 2. Let’s now consider ℓ=0.1,0.5,2,5,10 . A length-scale of 0.1 is very small relative to the range of the input domain we are considering, 25. For example, the values of the function at x=5 and x=10 will have essentially no correlation at such a length-scale. On the other hand, for a length-scale of 10, the function values at these inputs will be highly correlated. Note that the vertical scale changes in the following figures.

길이 척도를 변경하면 샘플 사전 및 사후 함수와 신뢰할 수 있는 세트에 어떤 영향을 미치는지 살펴보겠습니다. 위의 피팅은 길이 척도 2를 사용합니다. 이제 ℓ=0.1,0.5,2,5,10을 고려해 보겠습니다. 0.1의 길이 척도는 우리가 고려하고 있는 입력 영역의 범위인 25에 비해 매우 작습니다. 예를 들어 x=5와 x=10의 함수 값은 이러한 길이 척도에서 본질적으로 상관 관계가 없습니다. . 반면, 길이 척도가 10인 경우 이러한 입력의 함수 값은 높은 상관 관계를 갖습니다. 다음 그림에서는 수직 스케일이 변경됩니다.

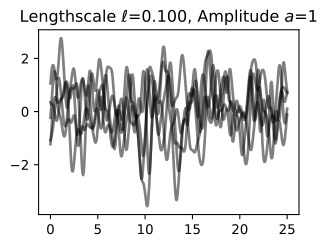
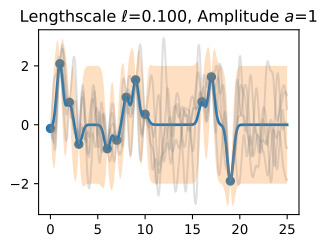
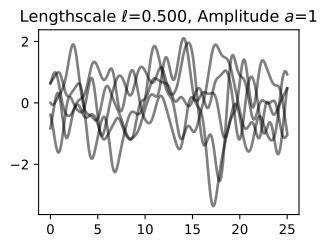
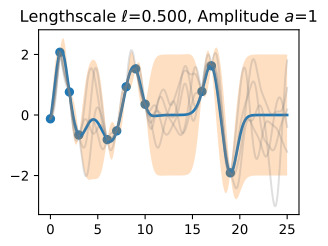
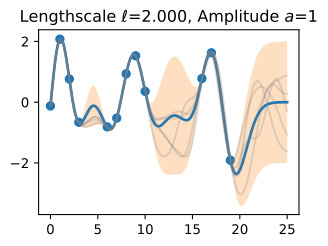
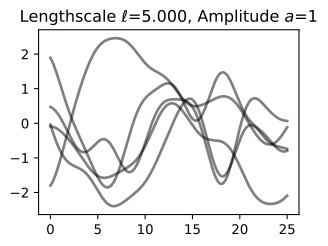
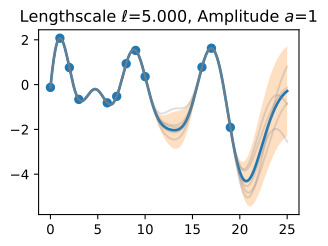
Notice as the length-scale increases the ‘wiggliness’ of the functions decrease, and our uncertainty decreases. If the length-scale is small, the uncertainty will quickly increase as we move away from the data, as the datapoints become less informative about the function values.

길이 척도가 증가함에 따라 함수의 '흔들림'이 감소하고 불확실성이 감소합니다. 길이 척도가 작으면 데이터 포인트가 함수 값에 대한 정보를 덜 제공하므로 데이터에서 멀어질수록 불확실성이 빠르게 증가합니다.

Now, let’s vary the amplitude parameter, holding the length-scale fixed at 2. Note the vertical scale is held fixed for the prior samples, and varies for the posterior samples, so you can clearly see both the increasing scale of the function, and the fits to the data.

이제 길이 스케일을 2로 고정하여 진폭 매개변수를 변경해 보겠습니다. 수직 스케일은 이전 샘플에 대해 고정되어 있고 사후 샘플에 대해 달라집니다. 따라서 함수의 스케일 증가와 데이터에 적합합니다.

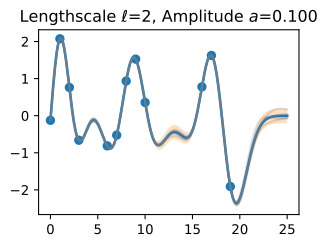
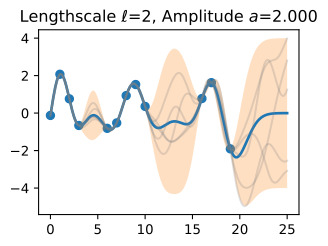
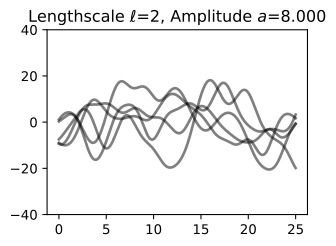
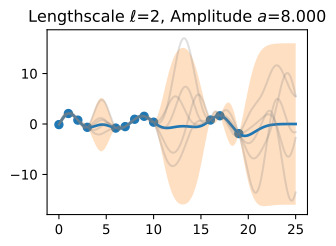
We see the amplitude parameter affects the scale of the function, but not the rate of variation. At this point, we also have the sense that the generalization performance of our procedure will depend on having reasonable values for these hyperparameters. Values of ℓ=2 and a=1 appeared to provide reasonable fits, while some of the other values did not. Fortunately, there is a robust and automatic way to specify these hyperparameters, using what is called the marginal likelihood, which we will return to in the notebook on inference.

진폭 매개변수는 함수의 규모에 영향을 주지만 변동률에는 영향을 미치지 않습니다. 이 시점에서 우리는 프로시저의 일반화 성능이 이러한 하이퍼파라미터에 대한 합리적인 값을 갖는지에 달려 있다는 것을 알게 되었습니다. ℓ=2 및 a=1 값은 합리적인 적합치를 제공하는 것으로 보였지만 일부 다른 값은 그렇지 않았습니다. 다행스럽게도 한계 우도(Marginal Likelihood)를 사용하여 이러한 하이퍼파라미터를 지정하는 강력하고 자동적인 방법이 있습니다. 이 방법은 추론에 대한 노트북에서 다시 설명하겠습니다.

So what is a GP, really? As we started, a GP simply says that any collection of function values f(x1),…,f(xn), indexed by any collection of inputs x1,…,xn has a joint multivariate Gaussian distribution. The mean vector μ of this distribution is given by a mean function, which is typically taken to be a constant or zero. The covariance matrix of this distribution is given by the kernel evaluated at all pairs of the inputs x.

그렇다면 GP란 무엇일까요? 우리가 시작했을 때, GP는 단순히 입력 x1,…,xn의 컬렉션에 의해 인덱스된 함수 값 f(x1),…,f(xn)의 컬렉션이 결합 다변량 가우스 분포를 갖는다고 말합니다. 이 분포의 평균 벡터 μ는 평균 함수로 제공되며 일반적으로 상수 또는 0으로 간주됩니다. 이 분포의 공분산 행렬은 모든 입력 x 쌍에서 평가된 커널에 의해 제공됩니다.

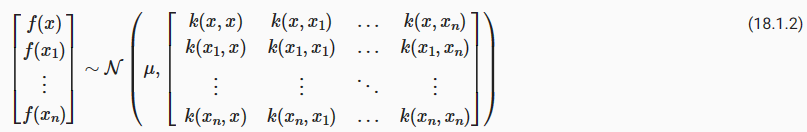
Equation (18.1.2) specifies a GP prior. We can compute the conditional distribution of f(x) for any x given f(x1),…,f(xn), the function values we have observed. This conditional distribution is called the posterior, and it is what we use to make predictions.

식 (18.1.2)은 GP 사전을 지정합니다. 우리가 관찰한 함수 값 f(x1),…,f(xn)이 주어지면 임의의 x에 대해 f(x)의 조건부 분포를 계산할 수 있습니다. 이 조건부 분포를 사후 분포라고 하며 예측을 위해 사용합니다.

In particular,  특히,

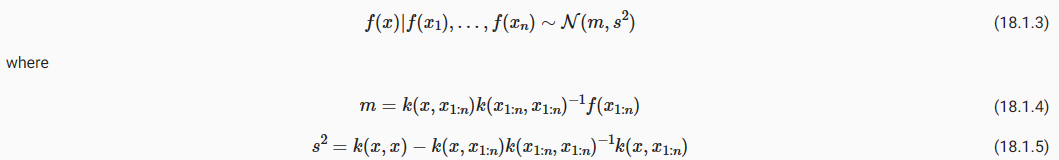
where k(x,x1:n) is a 1×n vector formed by evaluating k(x,xi) for i=1,…,n and k(x1:n,x1:n) is an n×n matrix formed by evaluating k(xi,xj) for i,j=1,…,n. m is what we can use as a point predictor for any x, and s**2 is what we use for uncertainty: if we want to create an interval with a 95% probability that f(x) is in the interval, we would use m±2s. The predictive means and uncertainties for all the above figures were created using these equations. The observed data points were given by f(x1),…,f(xn) and chose a fine grained set of x points to make predictions.

여기서 k(x,x1:n)은 i=1,…,n에 대해 k(x,xi)를 평가하여 형성된 1×n 벡터이고 k(x1:n,x1:n)은 형성된 n×n 행렬입니다. i,j=1,…,n에 대해 k(xi,xj)를 평가합니다. m은 임의의 x에 대한 점 예측자로 사용할 수 있는 것이고, s**2는 불확실성에 사용하는 것입니다. f(x)가 구간에 있을 확률이 95%인 구간을 생성하려면 다음과 같이 합니다. m±2초를 사용하세요. 위의 모든 수치에 대한 예측 평균과 불확실성은 이러한 방정식을 사용하여 생성되었습니다. 관찰된 데이터 포인트는 f(x1),…,f(xn)으로 제공되었으며 예측을 위해 세밀한 x 포인트 세트를 선택했습니다.

Let’s suppose we observe a single datapoint, f(x1), and we want to determine the value of f(x) at some x. Because f(x) is described by a Gaussian process, we know the joint distribution over (f(x),f(x1)) is Gaussian:

단일 데이터 포인트 f(x1)를 관찰하고 일부 x에서 f(x)의 값을 결정한다고 가정해 보겠습니다. f(x)는 가우스 프로세스로 설명되므로 (f(x),f(x1))에 대한 결합 분포가 가우스임을 알 수 있습니다.

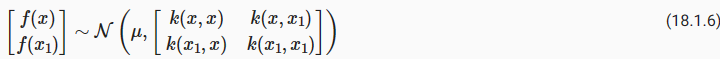
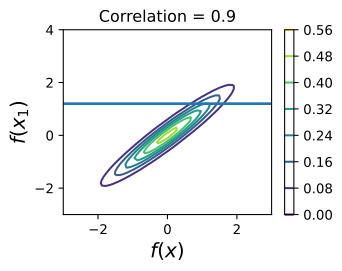
The off-diagonal expression k(x,x1)=k(x1,x) tells us how correlated the function values will be — how strongly determined f(x) will be from f(x1). We have seen already that if we use a large length-scale, relative to the distance between x and x1, ||x−x1||, then the function values will be highly correlated. We can visualize the process of determining f(x) from f(x1) both in the space of functions, and in the joint distribution over f(x1),f(x). Let’s initially consider an x such that k(x,x1)=0.9, and k(x,x)=1, meaning that the value of f(x) is moderately correlated with the value of f(x1). In the joint distribution, the contours of constant probability will be relatively narrow ellipses.

비대각선 표현식 k(x,x1)=k(x1,x)는 함수 값의 상관 관계, 즉 f(x)가 f(x1)에서 얼마나 강력하게 결정되는지 알려줍니다. 우리는 x와 x1 사이의 거리(||x−x1||)에 상대적으로 큰 길이 척도를 사용하면 함수 값의 상관 관계가 높다는 것을 이미 확인했습니다. 함수 공간과 f(x1),f(x)에 대한 결합 분포 모두에서 f(x1)에서 f(x)를 결정하는 프로세스를 시각화할 수 있습니다. 처음에 k(x,x1)=0.9, k(x,x)=1인 x를 고려해 보겠습니다. 이는 f(x) 값이 f(x1) 값과 중간 정도의 상관 관계가 있음을 의미합니다. 결합 분포에서 일정한 확률의 윤곽은 상대적으로 좁은 타원이 됩니다.

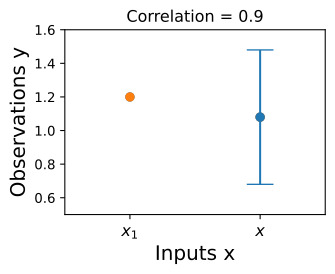
Suppose we observe f(x1)=1.2. To condition on this value of f(x1), we can draw a horizontal line at 1.2 on our plot of the density, and see that the value of f(x) is mostly constrained to [0.64,1.52]. We have also drawn this plot in function space, showing the observed point f(x1) in orange, and 1 standard deviation of the Gaussian process predictive distribution for f(x) in blue, about the mean value of 1.08.

f(x1)=1.2를 관찰한다고 가정합니다. 이 f(x1) 값을 조건으로 하기 위해 밀도 플롯에서 1.2에 수평선을 그릴 수 있으며 f(x) 값이 대부분 [0.64,1.52]로 제한되어 있음을 알 수 있습니다. 우리는 또한 이 플롯을 함수 공간에 그려서 관찰된 점 f(x1)을 주황색으로 표시하고 f(x)에 대한 가우스 프로세스 예측 분포의 1 표준 편차를 파란색으로 표시했습니다(평균값 약 1.08).

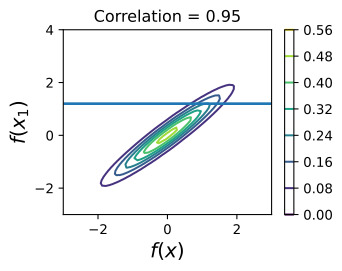
Now suppose we have a stronger correlation, k(x,x1)=0.95. Now the ellipses have narrowed further, and the value of f(x) is even more strongly determined by f(x1). Drawing a horizontal line at 1.2, we see the contours for f(x) support values mostly within [0.83,1.45]. Again, we also show the plot in function space, with one standard deviation about the mean predictive value of 1.14.

이제 k(x,x1)=0.95라는 더 강한 상관관계가 있다고 가정합니다. 이제 타원은 더 좁아졌고 f(x)의 값은 f(x1)에 의해 훨씬 더 강력하게 결정됩니다. 1.2에서 수평선을 그리면 f(x) 지원 값의 윤곽이 대부분 [0.83,1.45] 내에 있는 것을 볼 수 있습니다. 다시 말하지만, 평균 예측 값 1.14에 대한 표준 편차가 1인 함수 공간의 플롯도 표시됩니다.

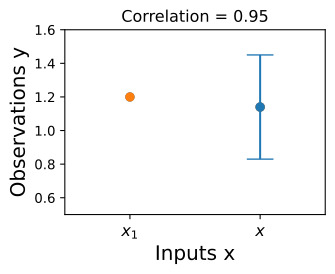
We see that the posterior mean predictor of our Gaussian process is closer to 1.2, because there is now a stronger correlation. We also see that our uncertainty (the error bars) have somewhat decreased. Despite the strong correlation between these function values, our uncertainty is still righly quite large, because we have only observed a single data point!

이제 더 강한 상관관계가 있기 때문에 가우스 프로세스의 사후 평균 예측 변수가 1.2에 더 가깝다는 것을 알 수 있습니다. 또한 불확실성(오차 막대)이 다소 감소한 것을 볼 수 있습니다. 이러한 함수 값 사이의 강한 상관 관계에도 불구하고 우리는 단 하나의 데이터 포인트만 관찰했기 때문에 불확실성은 여전히 상당히 큽니다!

This procedure can give us a posterior on f(x) for any x, for any number of points we have observed. Suppose we observe f(x1),f(x2). We now visualize the posterior for f(x) at a particular x=x′ in function space. The exact distribution for f(x) is given by the above equations. f(x) is Gaussian distributed, with mean

이 절차는 우리가 관찰한 임의의 수의 점에 대해 임의의 x에 대한 f(x)의 사후값을 제공할 수 있습니다. f(x1),f(x2)를 관찰한다고 가정합니다. 이제 함수 공간의 특정 x=x′에서 f(x)의 사후를 시각화합니다. f(x)의 정확한 분포는 위 방정식으로 제공됩니다. f(x)는 평균을 갖는 가우스 분포입니다.

and variance  및 분산

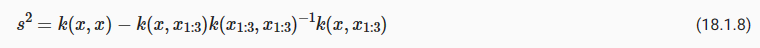
In this introductory notebook, we have been considering noise free observations. As we will see, it is easy to include observation noise. If we assume that the data are generated from a latent noise free function f(x) plus iid Gaussian noise ϵ(x)∼N(0,σ**2) with variance σ**2, then our covariance function simply becomes k(xi,xj)→k(xi,xj)+δijσ**2, where δif=1 if i=j and 0 otherwise.

이 소개 노트에서는 잡음 없는 관찰을 고려했습니다. 앞으로 살펴보겠지만 관찰 노이즈를 포함하는 것은 쉽습니다. 데이터가 잠재 잡음 없는 함수 f(x)와 분산 σ**2를 갖는 iid 가우스 잡음 ϵ(x)∼N(0,σ**2)에서 생성된다고 가정하면 공분산 함수는 간단히 k가 됩니다. (xi,xj)→k(xi,xj)+δijσ**2, 여기서 i=j이면 δif=1이고 그렇지 않으면 0입니다.

We have already started getting some intuition about how we can use a Gaussian process to specify a prior and posterior over solutions, and how the kernel function affects the properties of these solutions. In the following notebooks, we will precisely show how to specify a Gaussian process prior, introduce and derive various kernel functions, and then go through the mechanics of how to automatically learn kernel hyperparameters, and form a Gaussian process posterior to make predictions. While it takes time and practice to get used to concepts such as a “distributions over functions”, the actual mechanics of finding the GP predictive equations is actually quite simple — making it easy to get practice to form an intuitive understanding of these concepts.

우리는 이미 가우스 프로세스를 사용하여 솔루션에 대한 사전 및 사후를 지정하는 방법과 커널 기능이 이러한 솔루션의 속성에 어떻게 영향을 미치는지에 대한 직관을 얻기 시작했습니다. 다음 노트에서는 사전에 가우스 프로세스를 지정하는 방법, 다양한 커널 함수를 소개 및 도출하는 방법, 그리고 커널 하이퍼파라미터를 자동으로 학습하는 방법, 사후에 가우스 프로세스를 형성하여 예측하는 방법에 대한 메커니즘을 자세히 보여줍니다. "함수에 대한 분포"와 같은 개념에 익숙해지려면 시간과 연습이 필요하지만 GP 예측 방정식을 찾는 실제 메커니즘은 실제로 매우 간단하므로 이러한 개념을 직관적으로 이해하기 위한 연습을 쉽게 할 수 있습니다.

18.1.1. Summary

In typical machine learning, we specify a function with some free parameters (such as a neural network and its weights), and we focus on estimating those parameters, which may not be interpretable. With a Gaussian process, we instead reason about distributions over functions directly, which enables us to reason about the high-level properties of the solutions. These properties are controlled by a covariance function (kernel), which often has a few highly interpretable hyperparameters. These hyperparameters include the length-scale, which controls how rapidly (how wiggily) the functions are. Another hyperparameter is the amplitude, which controls the vertical scale over which our functions are varying. Representing many different functions that can fit the data, and combining them all together into a predictive distribution, is a distinctive feature of Bayesian methods. Because there is a greater amount of variability between possible solutions far away from the data, our uncertainty intuitively grows as we move from the data.

일반적인 기계 학습에서는 일부 자유 매개변수(예: 신경망 및 해당 가중치)를 사용하여 함수를 지정하고 해석할 수 없는 이러한 매개변수를 추정하는 데 중점을 둡니다. 가우스 프로세스를 사용하면 함수에 대한 분포를 직접 추론할 수 있으므로 솔루션의 상위 수준 속성을 추론할 수 있습니다. 이러한 속성은 해석 가능한 몇 가지 하이퍼 매개변수가 있는 공분산 함수(커널)에 의해 제어됩니다. 이러한 하이퍼파라미터에는 함수의 속도(얼마나 흔들리는지)를 제어하는 길이 척도가 포함됩니다. 또 다른 하이퍼파라미터는 진폭으로, 함수가 변하는 수직 스케일을 제어합니다. 데이터를 맞출 수 있는 다양한 함수를 표현하고 이를 모두 예측 분포로 결합하는 것은 베이지안 방법의 독특한 특징입니다. 데이터에서 멀리 떨어져 있는 가능한 솔루션 간에는 더 큰 변동성이 있기 때문에 데이터에서 이동할 때 불확실성이 직관적으로 커집니다.

A Gaussian process represents a distribution over functions by specifying a multivariate normal (Gaussian) distribution over all possible function values. It is possible to easily manipulate Gaussian distributions to find the distribution of one function value based on the values of any set of other values. In other words, if we observe a set of points, then we can condition on these points and infer a distribution over what the value of the function might look like at any other input. How we model the correlations between these points is determined by the covariance function and is what defines the generalization properties of the Gaussian process. While it takes time to get used to Gaussian processes, they are easy to work with, have many applications, and help us understand and develop other model classes, like neural networks.

가우스 프로세스는 가능한 모든 함수 값에 대해 다변량 정규(가우스) 분포를 지정하여 함수에 대한 분포를 나타냅니다. 가우스 분포를 쉽게 조작하여 다른 값 세트의 값을 기반으로 한 함수 값의 분포를 찾는 것이 가능합니다. 즉, 일련의 점을 관찰하면 이러한 점을 조건으로 하고 다른 입력에서 함수 값이 어떻게 보일지에 대한 분포를 추론할 수 있습니다. 이러한 점 간의 상관 관계를 모델링하는 방법은 공분산 함수에 의해 결정되며 이것이 가우스 프로세스의 일반화 속성을 정의합니다. 가우스 프로세스에 익숙해지는 데는 시간이 걸리지만 작업하기 쉽고 응용 프로그램이 많으며 신경망과 같은 다른 모델 클래스를 이해하고 개발하는 데 도움이 됩니다.

18.1.2. Exercises

1. What is the difference between epistemic uncertainty versus observation uncertainty?
2. Besides rate of variation and amplitude, what other properties of functions might we want to consider, and what would be real-world examples of functions that have those properties?
3. The RBF covariance function we considered says that covariances (and correlations) between observations decrease with their distance in the input space (times, spatial locations, etc.). Is this a reasonable assumption? Why or why not?
4. Is a sum of two Gaussian variables Gaussian? Is a product of two Gaussian variables Gaussian? If (a,b) have a joint Gaussian distribution, is a|b (a given b) Gaussian? Is a Gaussian?

6. Do you think increasing our estimate of observation noise would increase or decrease our estimate of the length-scale of the ground truth function?

7. As we move away from the data, suppose the uncertainty in our predictive distribution increases to a point, then stops increasing. Why might that happen?

https://d2l.ai/chapter_gaussian-processes/index.html

18. Gaussian Processes

Andrew Gordon Wilson (New York University and Amazon)

Gaussian processes (GPs) are ubitiquous. You have already encountered many examples of GPs without realizing it. Any model that is linear in its parameters with a Gaussian distribution over the parameters is a Gaussian process. This class spans discrete models, including random walks, and autoregressive processes, as well as continuous models, including Bayesian linear regression models, polynomials, Fourier series, radial basis functions, and even neural networks with an infinite number of hidden units. There is a running joke that “everything is a special case of a Gaussian process”.

가우스 프로세스(GP)는 어디에나 있습니다. 당신은 이미 깨닫지 못한 채 GP의 많은 예를 접했습니다. 매개변수에 대한 가우스 분포를 갖는 매개변수가 선형인 모든 모델은 가우스 프로세스입니다. 이 클래스는 베이지안 선형 회귀 모델, 다항식, 푸리에 급수, 방사형 기저 함수 및 무한한 수의 숨겨진 단위가 있는 신경망을 포함한 연속 모델뿐만 아니라 랜덤 워크 및 자동 회귀 프로세스를 포함한 이산 모델을 포괄합니다. "모든 것은 가우스 과정의 특별한 경우이다"라는 농담이 있습니다.

Learning about Gaussian processes is important for three reasons: (1) they provide a function space perspective of modelling, which makes understanding a variety of model classes, including deep neural networks, much more approachable; (2) they have an extraordinary range of applications where they are state-of-the-art, including active learning, hyperparameter learning, auto-ML, and spatiotemporal regression; (3) over the last few years, algorithmic advances have made Gaussian processes increasingly scalable and relevant, harmonizing with deep learning through frameworks such as GPyTorch (Gardner et al., 2018). Indeed, GPs and and deep neural networks are not competing approaches, but highly complementary, and can be combined to great effect. These algorithmic advances are not just relevant to Gaussian processes, but provide a foundation in numerical methods that is broadly useful in deep learning.

가우스 프로세스에 대해 배우는 것은 세 가지 이유로 중요합니다. (1) 모델링의 함수 공간 관점을 제공하여 심층 신경망을 포함한 다양한 모델 클래스를 훨씬 더 쉽게 이해할 수 있습니다. (2) 능동 학습, 하이퍼파라미터 학습, 자동 ML 및 시공간 회귀를 포함하여 최첨단 애플리케이션에 적용할 수 있는 범위가 넓습니다. (3) 지난 몇 년 동안 알고리즘의 발전으로 인해 GPyTorch(Gardner et al., 2018)와 같은 프레임워크를 통해 딥 러닝과 조화를 이루면서 가우스 프로세스의 확장성과 관련성이 점점 더 높아졌습니다. 실제로 GP와 심층 신경망은 경쟁적인 접근 방식이 아니라 매우 상호보완적이며 결합하여 큰 효과를 낼 수 있습니다. 이러한 알고리즘의 발전은 가우스 프로세스에만 관련된 것이 아니라 딥 러닝에서 광범위하게 유용한 수치적 방법의 기초를 제공합니다.

In this chapter, we introduce Gaussian processes. In the introductory notebook, we start by reasoning intuitively about what Gaussian processes are and how they directly model functions. In the priors notebook, we focus on how to specify Gaussian process priors. We directly connect the tradiational weight-space approach to modelling to function space, which will help us reason about constructing and understanding machine learning models, including deep neural networks. We then introduce popular covariance functions, also known as kernels, which control the generalization properties of a Gaussian process. A GP with a given kernel defines a prior over functions. In the inference notebook, we will show how to use data to infer a posterior, in order to make predictions. This notebook contains from-scratch code for making predictions with a Gaussian process, as well as an introduction to GPyTorch. In upcoming notebooks, we will introduce the numerics behind Gaussian processes, which is useful for scaling Gaussian processes but also a powerful general foundation for deep learning, and advanced use-cases such as hyperparameter tuning in deep learning. Our examples will make use of GPyTorch, which makes Gaussian processes scale, and is closely integrated with deep learning functionality and PyTorch.

이번 장에서는 가우스 프로세스를 소개합니다. 입문 노트에서는 가우스 프로세스가 무엇인지, 그리고 이것이 기능을 직접 모델링하는 방법에 대해 직관적으로 추론하는 것부터 시작합니다. 사전 노트북에서는 가우스 프로세스 사전을 지정하는 방법에 중점을 둡니다. 우리는 모델링에 대한 전통적인 가중치 공간 접근 방식을 함수 공간에 직접 연결합니다. 이는 심층 신경망을 포함한 기계 학습 모델을 구성하고 이해하는 데 도움이 될 것입니다. 그런 다음 가우스 프로세스의 일반화 속성을 제어하는 커널이라고도 알려진 널리 사용되는 공분산 함수를 소개합니다. 주어진 커널을 가진 GP는 기능에 대한 사전 정의를 정의합니다. 추론 노트북에서는 예측을 위해 데이터를 사용하여 사후 추론을 수행하는 방법을 보여줍니다. 이 노트북에는 GPyTorch에 대한 소개뿐만 아니라 가우스 프로세스로 예측을 수행하기 위한 처음부터 시작하는 코드가 포함되어 있습니다. 다가오는 노트북에서는 가우스 프로세스를 확장하는 데 유용할 뿐만 아니라 딥 러닝을 위한 강력한 일반 기반이자 딥 러닝의 하이퍼파라미터 튜닝과 같은 고급 사용 사례인 가우스 프로세스 이면의 수치를 소개할 것입니다. 우리의 예에서는 가우시안 프로세스를 확장하고 딥 러닝 기능 및 PyTorch와 긴밀하게 통합되는 GPyTorch를 사용합니다.

Gaussian Processes 란?

**가우시안 프로세스(Gaussian Processes)**는 확률론적 모델링과 머신 러닝에서 사용되는 강력한 도구 중 하나입니다. 가우시안 프로세스는 데이터의 확률 분포를 모델링하고 예측하는 데 사용되며, 주로 회귀 문제 및 베이지안 최적화에 적용됩니다.

가우시안 프로세스는 확률적인 함수의 집합으로 정의되며, 이 함수들은 확률 분포에 따라서 결정됩니다. 각 함수는 무한한 차원의 입력 공간에서 정의되며, 이 함수들은 데이터 포인트의 무한한 집합에 대한 관측치를 설명하는 데 사용됩니다. 가우시안 프로세스는 다음과 같은 특징을 가집니다:

1. 확률적 모델: 가우시안 프로세스는 함수의 확률 분포를 모델링하며, 각 함수 값은 확률 변수로 취급됩니다. 이를 통해 불확실성을 포함한 예측을 수행할 수 있습니다.
2. 확률 분포의 파라미터: 가우시안 프로세스의 주요 파라미터는 평균 함수(일반적으로 0)와 공분산 함수(커널 함수)입니다. 이러한 함수들은 가우시안 프로세스의 형태와 성능을 결정하는 데 중요한 역할을 합니다.
3. 평활성 및 유연성: 가우시안 프로세스는 입력 공간에서 연속적이고 매끄러운 함수를 모델링하므로 노이즈가 있는 데이터에도 적합합니다. 이러한 성질은 회귀 문제에서 특히 유용합니다.
4. 확률적 예측: 가우시안 프로세스는 예측할 때 확률적 결과를 반환하며, 예측의 불확실성을 측정할 수 있습니다. 이를 통해 예측 신뢰도를 고려한 의사 결정을 내릴 수 있습니다.

가우시안 프로세스는 회귀, 분류, 최적화, 시뮬레이션 등 다양한 문제에 적용되며, 베이지안 하이퍼파라미터 최적화 및 함수 근사에도 사용됩니다. 가우시안 프로세스는 작은 데이터셋부터 대규모 데이터셋까지 다양한 문제에 유용하며, 머신 러닝 및 통계 분야에서 확장성과 강력한 예측 능력을 제공하는 중요한 도구 중 하나입니다.

https://d2l.ai/chapter_reinforcement-learning/qlearning.html

17.3. Q-Learning

In the previous section, we discussed the Value Iteration algorithm which requires accessing the complete Markov decision process (MDP), e.g., the transition and reward functions. In this section, we will look at Q-Learning (Watkins and Dayan, 1992) which is an algorithm to learn the value function without necessarily knowing the MDP. This algorithm embodies the central idea behind reinforcement learning: it will enable the robot to obtain its own data.

이전 섹션에서는 전체 마르코프 결정 프로세스(MDP)(예: 전환 및 보상 기능)에 액세스해야 하는 Value Iteration 알고리즘에 대해 논의했습니다. 이번 절에서는 MDP를 알지 못하는 상태에서 가치함수를 학습하는 알고리즘인 Q-Learning(Watkins and Dayan, 1992)을 살펴보겠습니다. 이 알고리즘은 강화 학습의 핵심 아이디어를 구현합니다. 이를 통해 로봇은 자체 데이터를 얻을 수 있습니다.

Q-Learning이란?

'Q-Learning'은 강화 학습(Reinforcement Learning)에서 사용되는 강화 학습 알고리즘 중 하나입니다. Q-Learning은 미래 보상을 고려하여 에이전트가 최적의 행동을 학습하는 데 사용됩니다.

Q-Learning의 주요 아이디어는 'Q-Value' 또는 'Action-Value' 함수를 학습하는 것입니다. 각 상태(State) 및 행동(Action)에 대한 Q-Value는 해당 상태에서 특정 행동을 선택했을 때 얻을 수 있는 예상 보상의 합계를 나타냅니다. Q-Value 함수는 다음과 같이 정의됩니다.

Q(s, a) = (1 - α) * Q(s, a) + α * (R + γ * max(Q(s', a')))

여기서:

• Q(s, a): 상태 s에서 행동 a를 선택할 때의 Q-Value입니다.
• α(알파): 학습률(learning rate)로, Q-Value를 업데이트할 때 현재 값과 새로운 값을 얼마나 가중치를 두고 합칠지 결정합니다.
• R: 현재 상태에서 행동을 수행했을 때 얻는 보상(reward)입니다.
• γ(감마): 감쇠 계수(discount factor)로, 미래 보상을 현재 보상보다 얼마나 가치 있게 여길지를 결정합니다.
• max(Q(s', a')): 다음 상태 s'에서 가능한 모든 행동 중에서 최대 Q-Value를 선택합니다.

Q-Learning 알고리즘의 주요 특징은 다음과 같습니다:

1. 모델-Fee: 환경에 대한 사전 지식 없이 직접 경험을 통해 학습합니다.
2. Off-Policy: 정책(policy)을 따라가는 것이 아니라, 최적의 정책을 찾기 위해 여러 정책을 시도하면서 학습합니다.
3. 탐험(Exploration)과 이용(Exploitation)의 균형: Q-Learning은 탐험을 통해 더 나은 행동을 찾으며, 이용을 통해 현재까지 학습된 지식을 활용합니다.

Q-Learning은 강화 학습의 고전적인 알고리즘 중 하나로, 다양한 응용 분야에서 사용됩니다. 특히, 게임이나 로봇 제어와 같은 영역에서 많이 활용되며, 강화 학습의 핵심 개념을 이해하는 데 도움이 됩니다.

17.3.1. The Q-Learning Algorithm

Recall that value iteration for the action-value function in Value Iteration corresponds to the update

Value Iteration에서 action-value function에 대한 value iteration은 업데이트에 해당한다는 점을 기억하세요.

As we discussed, implementing this algorithm requires knowing the MDP, specifically the transition function P(s′∣s,a). The key idea behind Q-Learning is to replace the summation over all s′∈S in the above expression by a summation over the states visited by the robot. This allows us to subvert the need to know the transition function.

논의한 대로 이 알고리즘을 구현하려면 MDP, 특히 전이 함수 P(s′∣s,a)를 알아야 합니다. Q-Learning의 핵심 아이디어는 위 표현식의 모든 s′∈S에 대한 합산을 로봇이 방문한 상태에 대한 합산으로 대체하는 것입니다. 이를 통해 우리는 전환 함수를 알아야 할 필요성을 뒤집을 수 있습니다.

17.3.2. An Optimization Problem Underlying Q-Learning

Let us imagine that the robot uses a policy πe(a∣s) to take actions. Just like the previous chapter, it collects a dataset of n trajectories of T timesteps each {(s**i t,a**i t)t=0,…,T−1}i=1,…,n. Recall that value iteration is really a set of constraints that ties together the action-value Q*(s,a) of different states and actions to each other. We can implement an approximate version of value iteration using the data that the robot has collected using πe as

로봇이 정책 πe(a∣s)를 사용하여 조치를 취한다고 가정해 보겠습니다. 이전 장과 마찬가지로 각 {(s**i t,a**i t)t=0,…,T−1}i=1,…,n T 시간 단계의 n 궤적 데이터 세트를 수집합니다. value iteration은 실제로 서로 다른 상태와 동작의 동작 값 Q*(s,a)를 서로 연결하는 제약 조건 집합이라는 점을 기억하세요. 로봇이 πe를 사용하여 수집한 데이터를 사용하여 대략적인 value iteration 버전을 구현할 수 있습니다.

Let us first observe the similarities and differences between this expression and value iteration above. If the robot’s policy πe were equal to the optimal policy π*, and if it collected an infinite amount of data, then this optimization problem would be identical to the optimization problem underlying value iteration. But while value iteration requires us to know P(s′∣s,a), the optimization objective does not have this term. We have not cheated: as the robot uses the policy πe to take an action a**i t at state s**i t, the next state s**i t+1 is a sample drawn from the transition function. So the optimization objective also has access to the transition function, but implicitly in terms of the data collected by the robot.

먼저 이 표현과 위의 값 반복 간의 유사점과 차이점을 살펴보겠습니다. 로봇의 정책 πe가 최적 정책 π*와 같고 무한한 양의 데이터를 수집했다면 이 최적화 문제는 가치 반복의 기본이 되는 최적화 문제와 동일할 것입니다. 그러나 값 반복을 위해서는 P(s′∣s,a)를 알아야 하지만 최적화 목적에는 이 항이 없습니다. 우리는 속이지 않았습니다. 로봇이 상태 s**i t에서 a**i t 작업을 수행하기 위해 정책 πe를 사용하므로 다음 상태 s**i t+1은 전이 함수에서 가져온 샘플입니다. 따라서 최적화 목표도 전환 기능에 액세스할 수 있지만 암시적으로 로봇이 수집한 데이터 측면에서 접근할 수 있습니다.

The variables of our optimization problem are Q(s,a) for all s∈S and a∈A. We can minimize the objective using gradient descent. For every pair (s**i t,a**i t) in our dataset, we can write

최적화 문제의 변수는 모든 s∈S 및 a∈A에 대한 Q(s,a)입니다. 경사 하강을 사용하여 목표를 최소화할 수 있습니다. 데이터 세트의 모든 쌍(s**i t,a**i t)에 대해 다음과 같이 쓸 수 있습니다.

where α is the learning rate. Typically in real problems, when the robot reaches the goal location, the trajectories end. The value of such a terminal state is zero because the robot does not take any further actions beyond this state. We should modify our update to handle such states as

여기서 α는 학습률입니다. 일반적으로 실제 문제에서는 로봇이 목표 위치에 도달하면 궤도가 종료됩니다. 로봇이 이 상태를 넘어서는 추가 작업을 수행하지 않기 때문에 이러한 최종 상태의 값은 0입니다. 다음과 같은 상태를 처리하려면 업데이트를 수정해야 합니다.

where 𝟙 s**i t+1 is terminal is an indicator variable that is one if s**i t+1 is a terminal state and zero otherwise. The value of state-action tuples (s,a) that are not a part of the dataset is set to −∞. This algorithm is known as Q-Learning.

여기서 𝟙 s**i t+1 is 터미널은 s**i t+1이 터미널 상태이면 1이고 그렇지 않으면 0인 표시 변수입니다. 데이터세트의 일부가 아닌 상태-동작 튜플(s,a)의 값은 −무효로 설정됩니다. 이 알고리즘은 Q-Learning으로 알려져 있습니다.

Given the solution of these updates Q^, which is an approximation of the optimal value function Q*, we can obtain the optimal deterministic policy corresponding to this value function easily using

최적의 가치 함수 Q*의 근사치인 이러한 업데이트 Q^의 솔루션이 주어지면 다음을 사용하여 이 가치 함수에 해당하는 최적의 결정론적 정책을 쉽게 얻을 수 있습니다.

There can be situations when there are multiple deterministic policies that correspond to the same optimal value function; such ties can be broken arbitrarily because they have the same value function.

동일한 최적 가치 함수에 해당하는 여러 결정론적 정책이 있는 상황이 있을 수 있습니다. 이러한 관계는 동일한 가치 함수를 갖기 때문에 임의로 끊어질 수 있습니다.

17.3.3. Exploration in Q-Learning

The policy used by the robot to collect data πe is critical to ensure that Q-Learning works well. Afterall, we have replaced the expectation over s′ using the transition function P(s′∣s,a) using the data collected by the robot. If the policy πe does not reach diverse parts of the state-action space, then it is easy to imagine our estimate Q^ will be a poor approximation of the optimal Q*. It is also important to note that in such a situation, the estimate of Q* at all states s∈S will be bad, not just the ones visited by πe. This is because the Q-Learning objective (or value iteration) is a constraint that ties together the value of all state-action pairs. It is therefore critical to pick the correct policy πe to collect data.

Q-Learning이 제대로 작동하려면 로봇이 데이터 πe를 수집하는 데 사용하는 정책이 중요합니다. 결국 우리는 로봇이 수집한 데이터를 사용하여 전이 함수 P(s′∣s,a)를 사용하여 s′에 대한 기대값을 대체했습니다. 정책 πe가 상태-행동 공간의 다양한 부분에 도달하지 못한다면 우리의 추정치 Q^가 최적 Q*에 대한 잘못된 근사치일 것이라고 상상하기 쉽습니다. 그러한 상황에서는 πe가 방문한 상태뿐만 아니라 모든 상태 s∈S에서 Q*의 추정값이 나쁠 것이라는 점에 유의하는 것도 중요합니다. 이는 Q-Learning 목표(또는 값 반복)가 모든 상태-작업 쌍의 값을 하나로 묶는 제약 조건이기 때문입니다. 따라서 데이터를 수집하기 위해 올바른 정책을 선택하는 것이 중요합니다.

We can mitigate this concern by picking a completely random policy πe that samples actions uniformly randomly from A. Such a policy would visit all states, but it will take a large number of trajectories before it does so.

우리는 A에서 균일하게 무작위로 작업을 샘플링하는 완전히 무작위적인 정책 πe를 선택하여 이러한 우려를 완화할 수 있습니다. 이러한 정책은 모든 상태를 방문하지만 그렇게 하기 전에 많은 수의 궤적을 필요로 합니다.

We thus arrive at the second key idea in Q-Learning, namely exploration. Typical implementations of Q-Learning tie together the current estimate of Q and the policy πe to set

where ε is called the “exploration parameter” and is chosen by the user. The policy πe is called an exploration policy. This particular πe is called an ε-greedy exploration policy because it chooses the optimal action (under the current estimate Q^) with probability 1−ε but explores randomly with the remainder probability ε. We can also use the so-called softmax exploration policy

여기서 ε는 "탐색 매개변수"라고 하며 사용자가 선택합니다. 정책 πe를 탐사 정책이라고 합니다. 이 특정 πe는 확률 1−ε로 최적의 행동(현재 추정치 Q^ 하에서)을 선택하지만 나머지 확률 ε으로 무작위로 탐색하기 때문에 ε-탐욕 탐색 정책이라고 합니다. 소위 소프트맥스 탐색 정책을 사용할 수도 있습니다.

where the hyper-parameter T is called temperature. A large value of ε in ε-greedy policy functions similarly to a large value of temperature T for the softmax policy.

여기서 초매개변수 T를 온도라고 합니다. ε-탐욕 정책에서 ε의 큰 값은 소프트맥스 정책의 온도 T의 큰 값과 유사하게 기능합니다.

It is important to note that when we pick an exploration that depends upon the current estimate of the action-value function Q^, we need to resolve the optimization problem periodically. Typical implementations of Q-Learning make one mini-batch update using a few state-action pairs in the collected dataset (typically the ones collected from the previous timestep of the robot) after taking every action using πe.

행동-가치 함수 Q^의 현재 추정에 의존하는 탐색을 선택할 때 최적화 문제를 주기적으로 해결해야 한다는 점에 유의하는 것이 중요합니다. Q-Learning의 일반적인 구현은 πe를 사용하여 모든 작업을 수행한 후 수집된 데이터 세트(일반적으로 로봇의 이전 단계에서 수집된 데이터)의 몇 가지 상태-작업 쌍을 사용하여 하나의 미니 배치 업데이트를 수행합니다.

17.3.4. The “Self-correcting” Property of Q-Learning

The dataset collected by the robot during Q-Learning grows with time. Both the exploration policy πe and the estimate Q^ evolve as the robot collects more data. This gives us a key insight into why Q-Learning works well. Consider a state s: if a particular action a has a large value under the current estimate Q^(s,a), then both the ε-greedy and the softmax exploration policies have a larger probability of picking this action. If this action actually is not the ideal action, then the future states that arise from this action will have poor rewards. The next update of the Q-Learning objective will therefore reduce the value Q^(s,a), which will reduce the probability of picking this action the next time the robot visits state s. Bad actions, e.g., ones whose value is overestimated in Q^(s,a), are explored by the robot but their value is correct in the next update of the Q-Learning objective. Good actions, e.g., whose value Q^(s,a) is large, are explored more often by the robot and thereby reinforced. This property can be used to show that Q-Learning can converge to the optimal policy even if it begins with a random policy πe (Watkins and Dayan, 1992).

Q-Learning 중에 로봇이 수집한 데이터 세트는 시간이 지남에 따라 증가합니다. 탐색 정책 πe와 추정치 Q^는 모두 로봇이 더 많은 데이터를 수집함에 따라 진화합니다. 이는 Q-Learning이 왜 잘 작동하는지에 대한 중요한 통찰력을 제공합니다. 상태 s를 고려하십시오. 특정 작업 a가 현재 추정치 Q^(s,a)보다 큰 값을 갖는 경우 ε-탐욕 및 소프트맥스 탐색 정책 모두 이 작업을 선택할 확률이 더 높습니다. 만약 이 행동이 실제로 이상적인 행동이 아니라면, 이 행동에서 발생하는 미래 상태는 낮은 보상을 받게 될 것입니다. 따라서 Q-Learning 목표의 다음 업데이트는 Q^(s,a) 값을 줄여 로봇이 다음에 상태 s를 방문할 때 이 작업을 선택할 확률을 줄입니다. 나쁜 행동, 예를 들어 Q^(s,a)에서 값이 과대평가된 행동은 로봇에 의해 탐색되지만 그 값은 Q-Learning 목표의 다음 업데이트에서 정확합니다. 예를 들어 Q^(s,a) 값이 큰 좋은 행동은 로봇에 의해 더 자주 탐색되어 강화됩니다. 이 속성은 Q-Learning이 무작위 정책 πe로 시작하더라도 최적의 정책으로 수렴할 수 있음을 보여주는 데 사용될 수 있습니다(Watkins and Dayan, 1992).

This ability to not only collect new data but also collect the right kind of data is the central feature of reinforcement learning algorithms, and this is what distinguishes them from supervised learning. Q-Learning, using deep neural networks (which we will see in the DQN chapeter later), is responsible for the resurgence of reinforcement learning (Mnih et al., 2013).

새로운 데이터를 수집할 뿐만 아니라 올바른 종류의 데이터를 수집하는 이러한 능력은 강화 학습 알고리즘의 핵심 기능이며 지도 학습과 구별됩니다. 심층 신경망(나중에 DQN 장에서 볼 예정)을 사용하는 Q-Learning은 강화 학습의 부활을 담당합니다(Mnih et al., 2013).

17.3.5. Implementation of Q-Learning

We now show how to implement Q-Learning on FrozenLake from Open AI Gym. Note this is the same setup as we consider in Value Iteration experiment.

이제 Open AI Gym의 FrozenLake에서 Q-Learning을 구현하는 방법을 보여줍니다. 이는 Value Iteration 실험에서 고려한 것과 동일한 설정입니다.

%matplotlib inline
import random
import numpy as np
from d2l import torch as d2l

seed = 0  # Random number generator seed
gamma = 0.95  # Discount factor
num_iters = 256  # Number of iterations
alpha   = 0.9  # Learing rate
epsilon = 0.9  # Epsilon in epsilion gready algorithm
random.seed(seed)  # Set the random seed
np.random.seed(seed)

# Now set up the environment
env_info = d2l.make_env('FrozenLake-v1', seed=seed)

이 코드는 강화 학습 문제를 해결하기 위한 환경 설정을 합니다. 구체적으로는 FrozenLake-v1 환경에서 Q-Learning 알고리즘을 실행하기 위한 환경을 설정하는 부분입니다. 코드의 주요 요소를 설명하겠습니다.

• %matplotlib inline: 이 라인은 주피터 노트북(Jupyter Notebook)에서 그래프 및 플롯을 인라인으로 표시하도록 지시합니다.
• import random: 파이썬의 random 모듈을 가져옵니다. 이 모듈은 난수 생성과 관련된 함수를 제공합니다.
• import numpy as np: NumPy 라이브러리를 가져옵니다. NumPy는 과학적 계산을 위한 파이썬 라이브러리로, 다차원 배열과 관련된 기능을 제공합니다. 주로 행렬 연산과 숫자 계산에 사용됩니다.
• from d2l import torch as d2l: "d2l" 패키지에서 "torch" 모듈을 가져와서 "d2l"로 별명을 붙입니다. 이 패키지는 "Dive into Deep Learning" 책의 코드와 유틸리티 함수를 제공합니다.
• seed = 0: 랜덤 시드(seed)를 0으로 설정합니다. 시드를 설정하면 랜덤 함수 호출 결과가 항상 동일하게 유지됩니다. 이렇게 하면 실험의 재현성을 확보할 수 있습니다.
• gamma = 0.95: 감쇠 요인(gamma)을 설정합니다. 감쇠 요인은 미래 보상의 가치를 현재 보상의 가치보다 얼마나 가중치를 둘 것인지 결정하는 요소입니다.
• num_iters = 256: Q-Learning의 반복 횟수를 설정합니다. 즉, 학습을 몇 번 반복할 것인지를 결정합니다.
• alpha = 0.9: 학습률(learning rate)을 설정합니다. 학습률은 Q-Value를 업데이트할 때 현재 값과 새로운 값을 얼마나 가중치를 두고 합칠지를 결정하는 요소입니다.
• epsilon = 0.9: 엡실론(epsilon) 값을 설정합니다. 엡실론은 엡실론-그리디(epsilon-greedy) 알고리즘에서 사용되며, 탐험(Exploration)과 이용(Exploitation) 사이의 균형을 조절하는 역할을 합니다.
• random.seed(seed), np.random.seed(seed): 랜덤 시드를 설정하여 실험 결과의 재현성을 확보합니다. 같은 시드를 사용하면 같은 조건에서 항상 같은 결과를 얻을 수 있습니다.
• env_info = d2l.make_env('FrozenLake-v1', seed=seed): 'FrozenLake-v1'이라는 환경을 생성하고, 시드(seed)를 설정합니다. FrozenLake-v1은 강화 학습을 위한 환경으로, 얼어붙은 호수에서 목표 지점까지 에이전트를 이동시키는 과제를 제공합니다.

이제 이 설정된 환경에서 Q-Learning 알고리즘을 실행할 수 있습니다.

In the FrozenLake environment, the robot moves on a 4×4 grid (these are the states) with actions that are “up” (↑), “down” (→), “left” (←), and “right” (→). The environment contains a number of holes (H) cells and frozen (F) cells as well as a goal cell (G), all of which are unknown to the robot. To keep the problem simple, we assume the robot has reliable actions, i.e. P(s′∣s,a)=1 for all s∈S,a∈A. If the robot reaches the goal, the trial ends and the robot receives a reward of 1 irrespective of the action; the reward at any other state is 0 for all actions. The objective of the robot is to learn a policy that reaches the goal location (G) from a given start location (S) (this is s0) to maximize the return.

FrozenLake 환경에서 로봇은 "위"(↑), "아래"(→), "왼쪽"(←), "오른쪽"( →). 환경에는 다수의 구멍(H) 세포와 동결(F) 세포 및 목표 세포(G)가 포함되어 있으며, 이들 모두는 로봇에 알려지지 않습니다. 문제를 단순하게 유지하기 위해 로봇이 신뢰할 수 있는 동작을 한다고 가정합니다. 즉, 모든 s∈S,a∈A에 대해 P(s′∣s,a)=1입니다. 로봇이 목표에 도달하면 시험이 종료되고 로봇은 행동에 관계없이 1의 보상을 받습니다. 다른 상태에서의 보상은 모든 행동에 대해 0입니다. 로봇의 목적은 주어진 시작 위치(S)(이것은 s0)에서 목표 위치(G)에 도달하는 정책을 학습하여 수익을 극대화하는 것입니다.

We first implement ε-greedy method as follows:

def e_greedy(env, Q, s, epsilon):
    if random.random() < epsilon:
        return env.action_space.sample()

    else:
        return np.argmax(Q[s,:])

이 코드는 엡실론-그리디(epsilon-greedy) 알고리즘을 구현한 함수입니다. 이 알고리즘은 강화 학습에서 탐험(Exploration)과 이용(Exploitation) 사이의 균형을 조절하기 위해 사용됩니다. 엡실론-그리디 알고리즘은 주어진 상황에서 랜덤한 행동을 선택할 확률과 현재 학습한 최적 행동을 선택할 확률을 조절합니다.

여기서 각 인자의 의미를 설명하겠습니다:

• env: 강화 학습 환경입니다. 이 환경에서 에이전트는 행동을 선택하고 보상을 받습니다.
• Q: Q-Value 함수로, 각 상태(state) 및 행동(action)에 대한 가치를 나타내는 배열입니다. Q[s, a]는 상태 s에서 행동 a를 선택했을 때의 가치를 나타냅니다.
• s: 현재 상태를 나타내는 변수입니다.
• epsilon: 엡실론(epsilon) 값으로, [0, 1] 범위의 확률값입니다. 엡실론은 랜덤한 행동을 선택할 확률을 결정하는 매개변수입니다.

이 함수의 동작은 다음과 같습니다:

1. random.random() < epsilon: 랜덤한 확률값을 생성하고 이 값이 엡실론 값보다 작은지를 확인합니다. 엡실론 값보다 작으면 랜덤한 행동을 선택하게 됩니다. 이것은 탐험(Exploration)을 의미합니다. 즉, 에이전트는 새로운 경험을 얻기 위해 무작위로 행동을 선택합니다.
2. 엡실론 값보다 크면, Q-Value 함수를 통해 현재 상태 s에서 가능한 행동 중에서 가치가 가장 높은 행동을 선택합니다. 이것은 이용(Exploitation)을 의미합니다. 에이전트는 학습한 지식을 활용하여 최적의 행동을 선택합니다.

따라서 이 함수는 엡실론 확률에 따라 탐험과 이용을 조절하여 행동을 선택합니다.

We are now ready to implement Q-learning:

이제 Q-learning을 구현할 준비가 되었습니다.

def q_learning(env_info, gamma, num_iters, alpha, epsilon):
    env_desc = env_info['desc']  # 2D array specifying what each grid item means
    env = env_info['env']  # 2D array specifying what each grid item means
    num_states = env_info['num_states']
    num_actions = env_info['num_actions']

    Q  = np.zeros((num_states, num_actions))
    V  = np.zeros((num_iters + 1, num_states))
    pi = np.zeros((num_iters + 1, num_states))

    for k in range(1, num_iters + 1):
        # Reset environment
        state, done = env.reset(), False
        while not done:
            # Select an action for a given state and acts in env based on selected action
            action = e_greedy(env, Q, state, epsilon)
            next_state, reward, done, _ = env.step(action)

            # Q-update:
            y = reward + gamma * np.max(Q[next_state,:])
            Q[state, action] = Q[state, action] + alpha * (y - Q[state, action])

            # Move to the next state
            state = next_state
        # Record max value and max action for visualization purpose only
        for s in range(num_states):
            V[k,s]  = np.max(Q[s,:])
            pi[k,s] = np.argmax(Q[s,:])
    d2l.show_Q_function_progress(env_desc, V[:-1], pi[:-1])

q_learning(env_info=env_info, gamma=gamma, num_iters=num_iters, alpha=alpha, epsilon=epsilon)

이 코드는 Q-Learning 알고리즘을 구현하여 강화 학습을 수행하는 함수입니다. Q-Learning은 강화 학습에서 가치 반복(Value Iteration)을 기반으로 하는 모델-프리(Model-Free) 강화 학습 알고리즘 중 하나로, 에이전트가 최적의 행동을 학습하는 방법 중 하나입니다.

여기서 각 인자의 의미를 설명하겠습니다:

• env_info: 강화 학습 환경 정보입니다. 환경의 구조와 관련된 정보가 포함되어 있습니다.
• gamma: 감쇠 계수(Discount Factor)로서 미래 보상의 현재 가치에 대한 중요성을 조절하는 매개변수입니다.
• num_iters: 반복 횟수로서 학습을 몇 번 반복할지 결정하는 매개변수입니다.
• alpha: 학습률(learning rate)로서 Q-Value를 업데이트할 때 얼마나 큰 보정을 적용할지 결정하는 매개변수입니다.
• epsilon: 엡실론(epsilon) 값으로, 엡실론-그리디 알고리즘에서 랜덤한 탐험 확률을 나타냅니다.

이 함수는 다음과 같이 동작합니다:

1. 초기 Q-Value 함수(Q)와 가치 함수(V)를 0으로 초기화합니다. 또한 정책 함수(pi)를 0으로 초기화합니다.
2. 주어진 반복 횟수(num_iters)만큼 아래의 과정을 반복합니다:
   • 환경을 초기화하고 시작 상태(state)를 얻습니다.
   • 에이전트는 엡실론-그리디 알고리즘을 사용하여 현재 상태(state)에서 행동(action)을 선택합니다. 엡실론 확률에 따라 랜덤한 탐험 행동 또는 학습한 Q-Value를 기반으로 한 최적 행동을 선택합니다.
   • 선택한 행동을 환경에 적용하고 다음 상태(next_state), 보상(reward), 종료 여부(done) 등을 얻습니다.
   • Q-Value 업데이트를 수행합니다. Q-Learning의 핵심은 Q-Value 업데이트 공식인 Bellman Equation을 사용하여 Q-Value를 업데이트하는 것입니다. 새로운 가치(y)는 현재 보상(reward)과 다음 상태의 최대 Q-Value(gamma * np.max(Q[next_state,:]))를 합친 값으로 계산됩니다. 그리고 이 값을 사용하여 Q-Value를 업데이트합니다.
   • 다음 상태로 이동합니다.
3. 각 반복에서 가치 함수(V)와 정책 함수(pi)를 업데이트하고 시각화를 위해 저장합니다.

이렇게 반복적으로 Q-Value를 업데이트하고 최적의 정책을 학습하여 환경에서 에이전트가 최적의 행동을 선택할 수 있도록 합니다.

This result shows that Q-learning can find the optimal solution for this problem roughly after 250 iterations. However, when we compare this result with the Value Iteration algorithm’s result (see Implementation of Value Iteration), we can see that the Value Iteration algorithm needs way fewer iterations to find the optimal solution for this problem. This happens because the Value Iteration algorithm has access to the full MDP whereas Q-learning does not.

이 결과는 Q-learning이 대략 250번의 반복 후에 이 문제에 대한 최적의 솔루션을 찾을 수 있음을 보여줍니다. 그러나 이 결과를 Value Iteration 알고리즘의 결과(Value Iteration 구현 참조)와 비교하면 Value Iteration 알고리즘이 이 문제에 대한 최적의 솔루션을 찾기 위해 훨씬 더 적은 반복이 필요하다는 것을 알 수 있습니다. 이는 Value Iteration 알고리즘이 전체 MDP에 액세스할 수 있는 반면 Q-learning은 액세스할 수 없기 때문에 발생합니다.

17.3.6. Summary

Q-learning is one of the most fundamental reinforcement-learning algorithms. It has been at the epicenter of the recent success of reinforcement learning, most notably in learning to play video games (Mnih et al., 2013). Implementing Q-learning does not require that we know the Markov decision process (MDP), e.g., the transition and reward functions, completely.

Q-러닝은 가장 기본적인 강화학습 알고리즘 중 하나입니다. 이는 최근 강화 학습 성공의 진원지였으며, 특히 비디오 게임 학습에서 가장 두드러졌습니다(Mnih et al., 2013). Q-러닝을 구현하기 위해 MDP(Markov Decision Process)(예: 전환 및 보상 기능)를 완전히 알 필요는 없습니다.

https://d2l.ai/chapter_reinforcement-learning/value-iter.html

17.2. Value Iteration

In this section we will discuss how to pick the best action for the robot at each state to maximize the return of the trajectory. We will describe an algorithm called Value Iteration and implement it for a simulated robot that travels over a frozen lake.

이 섹션에서는 Return of the trajectory (궤적 반환)을 최대화하기 위해 각 state에서 robot에 대한 최상의 action을 선택하는 방법을 설명할 것입니다. Value Iteration이라는 알고리즘을 설명하고 이를 얼어붙은 호수 위를 이동하는 시뮬레이션 로봇에 대해 구현해 보겠습니다.

Value Iteration이란?

'Value Iteration(가치 반복)'은 강화 학습(Reinforcement Learning)에서 사용되는 동적 프로그래밍(Dynamic Programming) 알고리즘 중 하나입니다. 가치 반복은 마르코프 결정 과정(Markov Decision Process, MDP)에서 최적 가치 함수(optimal value function)를 근사화하기 위해 사용됩니다.

MDP에서 가치 함수(value function)는 각 상태(state)의 가치를 측정하며, 최적 가치 함수는 최상의 정책(policy)을 찾기 위한 중요한 개념입니다. 가치 반복은 다음 단계로 진행됩니다:

1. Initialization(초기화): 가치 함수를 초기화합니다. 보통 모든 상태의 가치를 0으로 초기화하거나 임의의 값으로 초기화합니다.
2. Iterative Update(반복 업데이트): 반복적으로 현재의 가치 함수를 업데이트합니다. 이 업데이트는 다음과 같은 벨만 최적 방정식(Bellman Optimality Equation)을 사용하여 이루어집니다.
   • 상태 가치 업데이트(State Value Update): 모든 상태에 대해 현재 상태의 가치를 주변 상태의 가치와 보상을 고려하여 업데이트합니다. 이때 가치 함수는 최대값을 가지는 방향으로 업데이트됩니다.
   • 행동 가치 업데이트(Action Value Update): 상태 대신 상태-행동 쌍(state-action pair)에 대한 가치 함수를 업데이트합니다. 이는 에이전트가 각 상태에서 가능한 모든 행동에 대한 가치를 나타냅니다.
3. Convergence(수렴): 가치 함수가 수렴할 때까지 반복 업데이트를 수행합니다. 일반적으로 두 가지 가치 함수 간의 차이가 어떤 임계값 이하로 작아질 때 알고리즘을 종료합니다.
4. Policy Extraction(정책 추출): 최적 가치 함수를 기반으로 최적 정책을 추출합니다. 이 최적 정책은 에이전트가 각 상태에서 어떤 행동을 선택해야 하는지를 나타냅니다.

가치 반복은 최적 정책과 최적 가치 함수를 찾는 강화 학습 문제에서 효과적으로 사용됩니다. 하지만 모든 가능한 상태-행동 쌍에 대해 가치 함수를 업데이트하므로 상태와 행동의 공간이 크면 계산 비용이 높을 수 있습니다.

Return of the trajectory 란?

In the context of hyperparameter optimization or any optimization process, the "trajectory" typically refers to the path or sequence of points that the optimizer explores during the search for the optimal solution. Each point on this trajectory corresponds to a specific configuration of hyperparameters, and the trajectory represents how the objective function (or some other evaluation metric) changes as the optimizer moves from one configuration to another.

하이퍼파라미터 최적화 또는 다른 최적화 과정에서 "궤적(trajectory)"은 일반적으로 옵티마이저가 최적해를 찾기 위해 탐색하는 지점 또는 순서를 나타냅니다. 이 궤적 상의 각 지점은 하이퍼파라미터의 특정 설정에 해당하며, 궤적은 옵티마이저가 한 설정에서 다른 설정으로 이동함에 따라 목적 함수(또는 다른 평가 지표)가 어떻게 변화하는지를 나타냅니다.

The "return of the trajectory" usually refers to the value of the objective function at the final point or configuration reached by the optimizer after its search process is complete. In the context of hyperparameter optimization, this would be the performance or error metric associated with the best set of hyperparameters found by the optimizer.

"궤적의 반환(return of the trajectory)"은 보통 최적화 과정이 완료된 후 옵티마이저가 도달한 최종 지점 또는 설정에서의 목적 함수 값을 나타냅니다. 하이퍼파라미터 최적화의 맥락에서 이것은 최적화 과정을 통해 찾은 하이퍼파라미터 집합으로 모델을 훈련할 때 얻는 성능 또는 에러 지표와 관련됩니다.

For example, if you're using a hyperparameter tuning algorithm to find the best hyperparameters for a machine learning model, the "return of the trajectory" would represent the final performance (e.g., accuracy, loss, etc.) achieved by the model when trained with the hyperparameters discovered by the optimization process.

예를 들어, 기계 학습 모델의 최적 하이퍼파라미터를 찾기 위해 하이퍼파라미터 튜닝 알고리즘을 사용 중이라면 "궤적의 반환"은 최적화 과정 중 발견된 하이퍼파라미터 집합으로 훈련된 모델의 최종 성능(정확도, 손실 등)을 나타낼 것입니다.

In summary, "return of the trajectory" is a way to describe the outcome or result of the optimization process, which is often measured by the performance achieved with the best set of hyperparameters found during the search.

요약하면, "궤적의 반환"은 최적화 과정의 결과 또는 최적화 과정 중 찾은 최상의 하이퍼파라미터 설정을 사용했을 때 얻는 성능으로, 최적화 과정의 결과물을 나타내는 방식입니다.

17.2.1. Stochastic Policy 확률적 정책

A stochastic policy denoted as π(a∣s) (policy for short) is a conditional distribution over the actions a∈A given the state s∈S, π(a∣s)≡P(a∣s). As an example, if the robot has four actions A= {go left, go down, go right, go up}. The policy at a state s∈S for such a set of actions A is a categorical distribution where the probabilities of the four actions could be [0.4,0.2,0.1,0.3]; at some other state s′∈S the probabilities π(a∣s′) of the same four actions could be [0.1,0.1,0.2,0.6]. Note that we should have ∑a π(a∣s)=1 for any state s. A deterministic policy is a special case of a stochastic policy in that the distribution π(a∣s) only gives non-zero probability to one particular action, e.g., [1,0,0,0] for our example with four actions.

π(a∣s)(간단히 정책)로 표시되는 확률론적 정책은 상태 s∈S, π(a∣s)=P(a∣s)가 주어지면 동작 a∈A에 대한 조건부 분포입니다. 예를 들어, 로봇에 4가지 동작 A= {왼쪽으로 이동, 아래로 이동, 오른쪽으로 이동, 위로 이동}이 있는 경우입니다. 그러한 일련의 행동 A에 대한 상태 s∈S의 정책은 네 가지 행동의 확률이 [0.4,0.2,0.1,0.3]이 될 수 있는 범주형 분포입니다. 다른 상태 s′∈S에서 동일한 네 가지 행동의 확률 π(a∣s′)는 [0.1,0.1,0.2,0.6]이 될 수 있습니다. 모든 상태 s에 대해 ∑a π(a∣s)=1이 있어야 합니다. 결정론적 정책은 분포 π(a∣s)가 하나의 특정 작업에만 0이 아닌 확률을 제공한다는 점에서 확률론적 정책의 특별한 경우입니다(예: 4개 작업이 있는 예시의 경우 [1,0,0,0]).

Stochastic Policy란?

In the context of reinforcement learning, a "stochastic policy" refers to a strategy or a set of rules that an agent uses to make decisions in an environment. What makes it "stochastic" is that it introduces an element of randomness or probability into the decision-making process.

Reinforcement learning(강화 학습)의 맥락에서 '확률적 정책'은 에이전트가 환경에서 의사 결정을 내리는 데 사용하는 전략이나 규칙을 가리킵니다. 이것이 '확률적'으로 만드는 것은 의사 결정 프로세스에 확률 또는 무작위성 요소를 도입한다는 것입니다.

In a stochastic policy, the agent doesn't make deterministic choices, where every action is known in advance. Instead, it selects actions based on a probability distribution. This means that even in the same state, the agent might choose different actions in different episodes or trials, reflecting the inherent uncertainty in the environment or the agent's own decision-making process.

확률적 정책에서 에이전트는 결정을 내릴 때 미리 모든 행동이 알려져 있는 결정적 선택을 하지 않습니다. 대신, 확률 분포를 기반으로 행동을 선택합니다. 이것은 동일한 상태에서라도 에이전트가 다른 에피소드나 시도에서 다른 행동을 선택할 수 있음을 의미하며, 이는 환경의 불확실성이나 에이전트 자체의 의사 결정 프로세스에 내재된 불확실성을 반영합니다.

Stochastic policies are often represented as probability distributions over possible actions. The agent samples from this distribution to select an action. The degree of randomness or variability in the policy can vary depending on the specific problem and learning algorithm. Stochastic policies can be advantageous in situations where variability in actions is desirable to explore the environment more effectively or handle uncertainties.

확률적 정책은 종종 가능한 행동에 대한 확률 분포로 표현됩니다. 에이전트는 이 분포에서 샘플링하여 행동을 선택합니다. 정책의 무작위성이나 변동성의 정도는 구체적인 문제 및 학습 알고리즘에 따라 다를 수 있습니다. 환경을 더 효과적으로 탐색하거나 불확실성을 다루기 위해 행동의 변동성이 바람직한 상황에서 확률적 정책을 사용하는 것이 유리할 수 있습니다.

In contrast, a "deterministic policy" would map each state directly to a specific action without any randomness, meaning that in the same state, the agent would always choose the same action.

반면, '결정적 정책'은 각 상태를 특정한 행동에 직접 매핑하며 어떠한 무작위성도 없이 특정한 행동을 선택한다는 것을 의미합니다.

Stochastic policies are commonly used in reinforcement learning algorithms, such as policy gradient methods, to enable exploration and adaptability in dynamic environments.

확률적 정책은 주로 정책 그래디언트 방법 등의 강화 학습 알고리즘에서 사용되며, 동적 환경에서의 탐색과 적응을 가능하게 하기 위해 활용됩니다.

17.2.2. Value Function

Imagine now that the robot starts at a state s0 and at each time instant, it first samples an action from the policy at∼π(st) and takes this action to result in the next state st+1. The trajectory τ=(s0,a0,r0,s1,a1,r1,…), can be different depending upon which particular action at is sampled at intermediate instants. We define the average return R(τ)=∑**∞ t=0 γ**t r(st,at) of all such trajectories

이제 로봇이 상태 s0에서 시작하고 매 순간마다 먼저 ∼π(st)의 정책에서 작업을 샘플링하고 이 작업을 수행하여 다음 상태 st+1을 생성한다고 상상해 보세요. 궤적 τ=(s0,a0,r0,s1,a1,r1,…)은 중간 순간에 샘플링되는 특정 동작에 따라 다를 수 있습니다. 우리는 그러한 모든 궤적의 평균 수익률 R(τ)=∑**킵 t=0 γ**t r(st,at)을 정의합니다.

where s t+1∼P(st+1∣st,at) is the next state of the robot and r(st,at) is the instantaneous reward obtained by taking action 'at' in state st at time t. This is called the “value function” for the policy π. In simple words, the value of a state s0 for a policy π, denoted by V**π(s0), is the expected ϒ-discounted return obtained by the robot if it begins at state s0 and takes actions from the policy π at each time instant.

여기서 s t+1∼P(st+1∣st,at)는 로봇의 다음 상태이고, r(st,at)는 시간 t에서 상태 st에서 'at' 행동을 취함으로써 얻은 순간 보상이다. 이를 정책 π에 대한 "가치 함수"라고 합니다. 간단히 말해서, V**π(s0)로 표시되는 정책 π에 대한 상태 s0의 값은 기대되는 ϒ-할인된 수익입니다. 이것은 로봇이 상태 s0에서 시작하고 매 순간마다 정책 π에서 조치를 취하는 경우 로봇에 의해 수행되는 것에 의해 얻어집니다.

We next break down the trajectory into two stages (i) the first stage which corresponds to s0→s1 upon taking the action a0, and (ii) a second stage which is the trajectory τ′=(s1,a1,r1,…) thereafter. The key idea behind all algorithms in reinforcement learning is that the value of state s0 can be written as the average reward obtained in the first stage and the value function averaged over all possible next states s1. This is quite intuitive and arises from our Markov assumption: the average return from the current state is the sum of the average return from the next state and the average reward of going to the next state. Mathematically, we write the two stages as

다음으로 궤도를 두 단계로 나눕니다. (i) 조치 a0을 취했을 때 s0→s1에 해당하는 첫 번째 단계, (ii) 궤도 τ'=(s1,a1,r1,…)인 두 번째 단계 - 이러한 상황이 계속 이어짐 . 강화 학습의 모든 알고리즘 뒤에 있는 핵심 아이디어는 상태 s0의 값이 첫 번째 단계에서 얻은 평균 보상으로 기록될 수 있고 가치 함수가 가능한 모든 다음 상태 s1에 대해 평균을 낼 수 있다는 것입니다. 이는 매우 직관적이며 Markov 가정에서 비롯됩니다. 현재 상태의 평균 수익은 다음 상태의 평균 수익과 다음 상태로 이동하는 평균 보상의 합입니다. 수학적으로 우리는 두 단계를 다음과 같이 씁니다.

This decomposition is very powerful: it is the foundation of the principle of dynamic programming upon which all reinforcement learning algorithms are based. Notice that the second stage gets two expectations, one over the choices of the action a0 taken in the first stage using the stochastic policy and another over the possible states s1 obtained from the chosen action. We can write (17.2.2) using the transition probabilities in the Markov decision process (MDP) as

이러한 분해는 매우 강력합니다. 이는 모든 강화 학습 알고리즘의 기반이 되는 동적 프로그래밍 원리의 기초입니다. 두 번째 단계에서는 확률론적 정책을 사용하여 첫 번째 단계에서 취한 행동 a0의 선택에 대한 기대와 선택한 행동에서 얻은 가능한 상태 s1에 대한 기대라는 두 가지 기대를 얻습니다. 마르코프 결정 과정(MDP)의 전환 확률을 사용하여 (17.2.2)를 다음과 같이 작성할 수 있습니다.

An important thing to notice here is that the above identity holds for all states s∈S because we can think of any trajectory that begins at that state and break down the trajectory into two stages.

여기서 주목해야 할 중요한 점은 위의 항등식이 모든 상태 s∈S에 대해 적용된다는 것입니다. 왜냐하면 우리는 해당 상태에서 시작하는 모든 궤적을 생각하고 궤적을 두 단계로 나눌 수 있기 때문입니다.

Value Function이란?

In the context of reinforcement learning, a "value function" is a fundamental concept used to estimate the expected cumulative rewards an agent can obtain when following a particular policy in an environment. Value functions are essential for making decisions and learning in reinforcement learning tasks.

강화 학습의 맥락에서 '가치 함수(Value Function)'는 특정 환경에서 특정 정책을 따를 때 에이전트가 기대하는 누적 보상을 추정하는 데 사용되는 기본 개념입니다. 가치 함수는 강화 학습 작업에서의 의사 결정 및 학습에 필수적입니다.

There are two main types of value functions:

주로 두 가지 유형의 가치 함수가 있습니다:

1. State-Value Function (V(s)): This function estimates the expected cumulative reward an agent can achieve when starting from a particular state and following a specific policy. In other words, V(s) quantifies the long-term desirability of being in a given state while following the chosen policy.
   
   상태 가치 함수 (V(s)): 이 함수는 특정 상태에서 시작하여 특정 정책을 따를 때 에이전트가 기대하는 누적 보상을 추정합니다. 다시 말해, V(s)는 선택한 정책을 따를 때 주어진 상태에 있을 때의 장기적인 바람직함을 측정합니다.
   
   
2. Action-Value Function (Q(s, a)): This function estimates the expected cumulative reward an agent can obtain by taking a particular action (a) in a specific state (s) and then following a specific policy. Q(s, a) measures the long-term desirability of taking a particular action in a given state while following the chosen policy.
   
   행동 가치 함수 (Q(s, a)): 이 함수는 특정 상태 (s)에서 특정 행동 (a)을 취한 다음 특정 정책을 따를 때 에이전트가 기대하는 누적 보상을 추정합니다. Q(s, a)는 주어진 상태에서 특정 행동을 취할 때 선택한 정책을 따를 때의 장기적인 바람직함을 측정합니다.
   
   

Value functions are crucial for various reinforcement learning algorithms, such as Q-learning and policy gradient methods. They serve as a foundation for evaluating and comparing different policies. By iteratively updating these value functions, an agent can learn to make better decisions and maximize its cumulative rewards in the environment.

가치 함수는 Q-러닝(Q-learning) 및 정책 그래디언트 방법과 같은 다양한 강화 학습 알고리즘에서 중요합니다. 이들은 서로 다른 정책을 평가하고 비교하는 데 기초를 제공합니다. 이러한 가치 함수를 반복적으로 업데이트함으로써 에이전트는 더 나은 결정을 내리고 환경에서 누적 보상을 최대화하는 방법을 학습할 수 있습니다.

The ultimate goal of reinforcement learning is often to find an optimal policy, which is a policy that maximizes the expected cumulative reward. Value functions are essential tools for achieving this goal because they help assess and improve policies based on their expected performance.

강화 학습의 궁극적인 목표는 종종 기대 누적 보상을 최대화하는 최적 정책을 찾는 것입니다. 가치 함수는 이 목표를 달성하기 위한 중요한 도구입니다.

17.2.3. Action-Value Function

In implementations, it is often useful to maintain a quantity called the “action value” function which is a closely related quantity to the value function. This is defined to be the average return of a trajectory that begins at s0 but when the action of the first stage is fixed to be 

구현에서는 가치 함수와 밀접하게 관련된 수량인 "액션 가치" 함수라는 수량을 유지하는 것이 유용한 경우가 많습니다. 이는 s0에서 시작하지만 첫 번째 단계의 동작이 다음과 같이 고정된 궤적의 평균 반환으로 정의됩니다.

note that the summation inside the expectation is from t=1,…,∞ because the reward of the first stage is fixed in this case. We can again break down the trajectory into two parts and write

이 경우 첫 번째 단계의 보상이 고정되어 있기 때문에 기대값 내부의 합은 t=1,...,부터라는 점에 유의하세요. 우리는 다시 궤적을 두 부분으로 나누고 다음과 같이 쓸 수 있습니다.

This version is the analog of (17.2.3) for the action value function.

이 버전은 동작 값 함수에 대한 (17.2.3)과 유사합니다.

Action Value Function이란?

In the context of reinforcement learning, the "Action-Value Function," often denoted as Q(s, a), represents the expected cumulative reward an agent can obtain by taking a specific action (a) in a particular state (s) and then following a specific policy. It quantifies the long-term desirability of taking a particular action in a given state while adhering to the chosen policy.

강화 학습의 맥락에서 '행동 가치 함수(Action-Value Function)'는 특정 상태 (s)에서 특정 행동 (a)을 취한 다음 특정 정책을 따를 때 에이전트가 기대하는 누적 보상을 나타냅니다. 이는 선택한 정책을 따를 때 주어진 상태에서 특정 행동을 취하는 것의 장기적인 바람직함을 측정합니다.

Here's a breakdown of the components of the Action-Value Function (Q(s, a)):

행동 가치 함수 (Q(s, a))의 구성 요소를 살펴보겠습니다:

• s (state): This is the current situation or configuration of the environment that the agent perceives.
  
  s (상태): 이것은 에이전트가 지각하는 환경의 현재 상황 또는 구성입니다.
  
  
• a (action): This is the specific action that the agent takes in the current state.
  
  a (행동): 이것은 에이전트가 현재 상태에서 취하는 구체적인 행동입니다.
  
  
• Q(s, a): This is the Action-Value Function, which provides an estimate of the expected cumulative reward starting from state s, taking action a, and then following a specific policy.
  
  Q(s, a): 이것은 행동 가치 함수로, 상태 s에서 행동 a를 취하고 특정 정책을 따를 때 기대하는 누적 보상을 추정합니다.
  
  

The Action-Value Function is fundamental in reinforcement learning because it helps the agent evaluate and compare different actions in a given state. By computing the Q-values for each action in each state and following a specific policy, an agent can make informed decisions to maximize its cumulative rewards over time.

행동 가치 함수는 강화 학습에서 기본적이며, 에이전트가 주어진 상태에서 다른 행동을 평가하고 비교하는 데 도움을 줍니다. 각 상태에서 각 행동의 Q-값을 계산하고 특정 정책을 따를 때, 에이전트는 시간이 지남에 따라 누적 보상을 최대화하기 위한 정보에 기반하여 결정을 내릴 수 있습니다.

One of the key algorithms that uses the Action-Value Function is Q-learning, which aims to learn the optimal action-value function (Q-function) that maximizes the expected cumulative reward. This function is often used to guide the agent's behavior in an environment, allowing it to learn to make better decisions over time.

행동 가치 함수를 사용하는 주요 알고리즘 중 하나는 Q-러닝(Q-learning)입니다. 이 알고리즘은 기대 누적 보상을 최대화하는 행동 가치 함수 (Q-함수)를 학습하는 것을 목표로 하며, 이 함수는 환경에서 에이전트의 행동을 안내하는 데 자주 사용됩니다. 에이전트는 시간이 지남에 따라 더 나은 결정을 내리도록 학습하게 됩니다.

17.2.4. Optimal Stochastic Policy

Both the value function and the action-value function depend upon the policy that the robot chooses. We will next think of the “optimal policy” that achieves the maximal average return

가치 함수와 행동-가치 함수는 모두 로봇이 선택하는 정책에 따라 달라집니다. 다음으로 최대 평균수익률을 달성하는 '최적정책'에 대해 생각해 보겠습니다.

Of all possible stochastic policies that the robot could have taken, the optimal policy π* achieves the largest average discounted return for trajectories starting from state s0. Let us denote the value function and the action-value function of the optimal policy as V*≡Vπ* and Q*≡Qπ*.

로봇이 취할 수 있는 모든 가능한 확률론적 정책 중에서 최적 정책 π*는 상태 s0에서 시작하는 궤도에 대해 가장 큰 평균 할인 수익을 달성합니다. 최적 정책의 가치함수와 행동-가치함수를 V*=Vπ* 및 Q*=Qπ*로 표시하겠습니다.

Let us observe that for a deterministic policy where there is only one action that is possible under the policy at any given state. This gives us

특정 상태의 정책에 따라 가능한 작업이 하나만 있는 결정론적 정책에 대해 살펴보겠습니다. 이것이 우리에게 이것을 줍니다.

A good mnemonic to remember this is that the optimal action at state s (for a deterministic policy) is the one that maximizes the sum of reward r(s,a) from the first stage and the average return of the trajectories starting from the next sate s′, averaged over all possible next states s′ from the second stage.

이것을 기억하기 위한 좋은 기억법은 상태 s(결정론적 정책에 대한)에서의 최적의 행동은 첫 번째 단계의 보상 r(s,a)의 합과 다음 단계부터 시작하는 궤적의 평균 반환을 최대화하는 행동이라는 것입니다. 상태 s'는 두 번째 단계에서 가능한 모든 다음 상태 s'에 대해 평균을 냅니다.

Optimal Stochastic Policy란?

An "optimal stochastic policy" in reinforcement learning refers to a strategy or set of rules that an agent follows in an environment to maximize its expected cumulative rewards while incorporating a certain level of randomness or probability into its decision-making process.

강화 학습에서 '최적 확률적 정책(Optimal Stochastic Policy)'은 에이전트가 환경에서 따르는 전략 또는 규칙을 나타내며, 기대 누적 보상을 극대화하기 위해 의사 결정 프로세스에 일정 수준의 무작위성 또는 확률성을 통합하는 것을 의미합니다.

Here's a breakdown of the key components of an optimal stochastic policy:

다음은 최적 확률적 정책의 주요 구성 요소를 설명한 것입니다:

1. Optimal: The policy is considered "optimal" when it achieves the highest expected cumulative reward over the long run. In other words, it is the best strategy among all possible policies the agent can follow in the given environment.
   
   최적: 정책은 장기적으로 기대 누적 보상을 최대화하는 경우에 "최적"으로 간주됩니다. 다시 말해, 주어진 환경에서 에이전트가 따를 수 있는 모든 정책 중에서 가장 우수한 전략입니다.
   
   
2. Stochastic: Unlike a deterministic policy that prescribes a single action for each state, an optimal stochastic policy introduces randomness or uncertainty into its actions. Instead of always selecting the same action in a given state, the agent chooses actions based on probability distributions. This stochasticity allows the agent to explore the environment effectively and adapt to uncertainties.
   
   확률적: 특정 상태에 대해 항상 동일한 행동을 규정하는 결정적 정책과 달리 최적 확률적 정책은 행동에 무작위성 또는 불확실성을 도입합니다. 주어진 상태에서 항상 동일한 행동을 선택하는 대신, 에이전트는 확률 분포를 기반으로 행동을 선택합니다. 이러한 확률성은 에이전트가 환경을 효과적으로 탐색하고 불확실성에 적응하는 데 도움이 됩니다.
   
   
3. Expected Cumulative Rewards: The primary objective of an optimal stochastic policy is to maximize the expected cumulative rewards or the expected return. This means that the policy aims to make decisions that, on average, lead to the highest possible total rewards over time.
   
   기대 누적 보상: 최적 확률적 정책의 주요 목표는 기대 누적 보상 또는 기대 수익을 극대화하는 것입니다. 이는 정책이 평균적으로 시간이 지남에 따라 가능한 최대 총 보상을 얻도록 결정을 내리려는 것을 의미합니다.
   
   

An optimal stochastic policy is often challenging to find and depends on the specific problem and the agent's understanding of the environment. It's typically determined using reinforcement learning algorithms that aim to estimate or approximate the optimal policy. These algorithms iteratively adjust the policy to find the best balance between exploration (trying out different actions) and exploitation (choosing actions that are known to yield high rewards) while considering the inherent uncertainty in the environment.

최적 확률적 정책을 찾는 것은 종종 어렵고 구체적인 문제 및 에이전트의 환경 이해에 따라 다릅니다. 이러한 정책을 추정하거나 근사하는 강화 학습 알고리즘을 사용하여 일반적으로 결정됩니다. 이러한 알고리즘은 환경의 내재적 불확실성을 고려하면서 탐색(다른 행동을 시도)과 활용(고 보상을 얻을 것으로 알려진 행동 선택) 사이의 최적 균형을 찾기 위해 정책을 반복적으로 조정합니다.

In summary, an optimal stochastic policy is a strategy that, over the long term, maximizes an agent's expected cumulative rewards while allowing for probabilistic decision-making, making it well-suited for reinforcement learning problems where exploration and adaptability are critical.

요약하면, 최적 확률적 정책은 기대 누적 보상을 최대화하면서 확률적 의사 결정을 허용하는 전략으로, 탐색과 적응이 중요한 강화 학습 문제에 적합합니다.

17.2.5. Principle of Dynamic Programming

Our developement in the previous section in (17.2.2) or (17.2.5) can be turned into an algorithm to compute the optimal value function V* or the action-value function Q*, respectively. Observe that

이전 섹션 (17.2.2) 또는 (17.2.5)의 개발은 각각 최적 가치 함수 V* 또는 행동-가치 함수 Q*를 계산하는 알고리즘으로 바뀔 수 있습니다. 그것을 관찰하십시오

For a deterministic optimal policy π*, since there is only one action that can be taken at state s, we can also write

결정론적 최적 정책 π*의 경우 상태 s에서 취할 수 있는 행동은 단 하나뿐이므로 다음과 같이 쓸 수도 있습니다.

for all states s∈S. This identity is called the “principle of dynamic programming” (Bellman, 1952, Bellman, 1957). It was formulated by Richard Bellman in 1950s and we can remember it as “the remainder of an optimal trajectory is also optimal”.

모든 상태 s∈S에 대해. 이러한 정체성을 "동적 프로그래밍의 원리"라고 합니다(Bellman, 1952, Bellman, 1957). 이는 1950년대 Richard Bellman에 의해 공식화되었으며 "최적 궤적의 나머지 부분도 최적"이라고 기억할 수 있습니다.

Principle of Dynamic Programming 이란?

The "Principle of Dynamic Programming" is a fundamental concept in the field of reinforcement learning and optimization, particularly in the context of solving problems with overlapping subproblems, such as many dynamic programming and reinforcement learning problems. It was first introduced by Richard Bellman in the mid-20th century.

'동적 프로그래밍 원리(Principle of Dynamic Programming)'는 강화 학습과 최적화 분야에서의 기본 개념으로, 많은 동적 프로그래밍과 강화 학습 문제와 같이 하위 문제가 겹치는 문제를 해결하기 위한 것입니다. 이 원리는 리처드 벨먼(Richard Bellman)에 의해 20세기 중반에 처음 소개되었습니다.

Dynamic programming is a mathematical optimization technique used to solve problems by breaking them down into smaller, overlapping subproblems and solving each subproblem only once, storing the results to avoid redundant computations. The Principle of Dynamic Programming consists of the following key components:

동적 프로그래밍은 문제를 더 작고 겹치는 하위 문제로 분해하고 각 하위 문제를 한 번만 해결하여 결과를 중복 계산하지 않도록 하는 수학적 최적화 기술입니다. 동적 프로그래밍의 원리는 다음과 같은 주요 구성 요소로 구성됩니다:

1. Optimality Principle: This principle states that an optimal solution to a larger problem can be constructed from optimal solutions to its smaller subproblems. In other words, it suggests that when solving a complex problem, you can build the solution incrementally by solving smaller subproblems optimally and then combining their solutions.
   
   최적성 원리: 이 원리는 큰 문제의 최적 해결책을 더 작은 하위 문제의 최적 해결책으로 구성할 수 있다고 말합니다. 다시 말해, 복잡한 문제를 해결할 때, 더 작은 하위 문제를 최적으로 해결하고 그들의 해결책을 결합하여 솔루션을 점진적으로 구성할 수 있다는 것을 제안합니다.
   
   
2. Overlapping Subproblems: Dynamic programming is particularly useful when the problem can be divided into subproblems that are reused multiple times during the solution process. By solving these subproblems once and storing their solutions, you can avoid redundant calculations.
   
   겹치는 하위 문제: 동적 프로그래밍은 문제를 해결하는 동안 여러 번 재사용되는 하위 문제로 나눌 수 있는 경우 특히 유용합니다. 이러한 하위 문제를 한 번 해결하고 그 결과를 저장하여 중복 계산을 피할 수 있습니다.
   
   
3. Memoization: To implement dynamic programming efficiently, you often use memoization, which involves storing the results of solved subproblems in a table or cache. When a subproblem is encountered again, you can simply look up its solution in the table instead of recomputing it.
   
   메모이제이션: 동적 프로그래밍을 효율적으로 구현하기 위해 해결된 하위 문제의 결과를 테이블이나 캐시에 저장하는 메모이제이션을 종종 사용합니다. 하위 문제가 다시 발견되면 결과를 다시 계산하는 대신 테이블에서 해결책을 찾을 수 있습니다.
   
   
4. Bottom-Up or Top-Down Approach: Dynamic programming can be approached in two main ways: bottom-up and top-down. In the bottom-up approach, you start by solving the smallest subproblems and progressively build up to the larger problem. In the top-down approach (also known as memoization), you start with the larger problem and recursively solve smaller subproblems, storing their results along the way.
   
   하향식 또는 상향식 접근법: 동적 프로그래밍은 주로 두 가지 주요 방식으로 접근할 수 있습니다. 하향식 접근법에서는 가장 작은 하위 문제부터 시작하여 점진적으로 큰 문제를 해결합니다. 상향식 접근법(메모이제이션으로도 알려집니다)에서는 큰 문제부터 시작하여 재귀적으로 작은 하위 문제를 해결하고 그 결과를 저장합니다.
   
   

Dynamic programming is used to solve a wide range of optimization problems, such as finding the shortest path in a graph (e.g., Dijkstra's algorithm), solving the knapsack problem, and in reinforcement learning for finding optimal policies and value functions. It's a powerful technique for tackling complex problems by efficiently reusing solutions to subproblems, and it forms the foundation for many algorithms in computer science and operations research.

동적 프로그래밍은 그래프에서 최단 경로를 찾는 문제(예: Dijkstra 알고리즘), 배낭 문제를 해결하는 문제 및 강화 학습에서 최적 정책과 가치 함수를 찾는 데 사용됩니다. 이것은 하위 문제의 솔루션을 효율적으로 재사용함으로써 복잡한 문제에 접근하는 강력한 기술이며, 컴퓨터 과학과 운영 연구의 많은 알고리즘의 기초를 형성합니다.

Bellman Equation 이란?

The Bellman Equation is a fundamental concept in the field of dynamic programming and reinforcement learning. It is named after the mathematician and computer scientist Richard Bellman. The Bellman Equation is a recursive equation used to express the total expected reward (or value) of being in a particular state of a system and taking a specific action, considering all possible future states and actions.

벨만 방정식(Bellman Equation)**은 동적 프로그래밍과 강화 학습 분야에서의 기본 개념입니다. 이 방정식은 수학자이자 컴퓨터 과학자인 리처드 벨만(Richard Bellman)의 이름에서 따왔습니다. 벨만 방정식은 특정 상태(state)에 있을 때 특정 동작(action)을 취하고 모든 가능한 미래 상태와 동작을 고려하여 예상 보상(또는 가치)의 총합을 표현하는 재귀적인 방정식입니다.

In its simplest form, the Bellman Equation is expressed as:

가장 간단한 형태로 벨만 방정식은 다음과 같이 표현됩니다:

V(s)=maxa​(R(s,a)+γ∑s′​P(s′∣s,a)V(s′))

Where:

• V(s) represents the value of being in state s, which is the expected cumulative reward from that state onward.
  
  V(s)는 상태 s에 있을 때의 가치를 나타내며, 해당 상태 이후의 예상 누적 보상입니다.
  
  
• a represents the action taken in state s.
  
  a는 상태 s에서 취한 동작을 나타냅니다.
  
  
• R(s,a) is the immediate reward obtained after taking action a in state s.
  
  R(s,a)은 상태 s에서 동작 a를 수행한 후 얻은 즉각적인 보상입니다.
  
  
• γ is the discount factor, which scales the importance of future rewards relative to immediate rewards.
  
  γ는 할인 계수로, 미래 보상의 중요성을 즉각적인 보상에 대비해 어떻게 조절할지를 나타냅니다.
  
  
• ∑s′​ represents a sum over all possible future states s′ that could be reached from state s by taking action a.
  
  ∑s′​은 동작 a를 취하여 상태 s에서 도달할 수 있는 모든 가능한 미래 상태 s′에 대한 합계를 나타냅니다.
  
  
• P(s′∣s,a) is the probability of transitioning from state s to state s′ when taking action a.
  
  P(s′∣s,a)는 동작 a를 취하면 상태 s에서 상태 s′로 전환할 확률입니다.
  
  
• V(s′) is the value of the next state s′.
  
  V(s′)은 다음 상태 s′의 가치를 나타냅니다.
  
  

The Bellman Equation provides a way to compute the value of each state in a sequential decision-making process, such as a Markov Decision Process (MDP). Solving the Bellman Equation is essential for finding the optimal policy, which is a mapping of states to actions that maximizes the expected cumulative reward over time.

벨만 방정식은 순차적 의사 결정 문제, 예를 들어 마르코프 결정 과정(Markov Decision Process, MDP)에서 각 상태의 가치를 계산하는 방법을 제공합니다. 벨만 방정식을 해결하는 것은 최적 정책을 찾는 데 필수적이며, 이 정책은 시간에 따른 누적 보상을 최대화하는 상태에서 동작으로의 매핑입니다.

The Bellman Equation is a key concept in reinforcement learning, where agents learn to make decisions by iteratively updating their value estimates based on observed rewards and transitions. It is a cornerstone of algorithms like Q-learning and the Bellman equation-based methods, which are widely used in artificial intelligence and robotics for solving sequential decision-making problems.

벨만 방정식은 강화 학습에서 중요한 개념으로, 에이전트는 관찰된 보상과 전이에 기반하여 가치 추정치를 반복적으로 업데이트하는 방식으로 의사 결정을 내리는 방법을 학습합니다. 이 방정식은 Q-러닝(Q-learning)과 벨만 방정식 기반 방법과 같은 알고리즘에서 핵심 개념으로 사용되며, 순차적 의사 결정 문제를 해결하기 위해 인공 지능과 로봇 공학 분야에서 널리 사용됩니다.

17.2.6. Value Iteration

We can turn the principle of dynamic programming into an algorithm for finding the optimal value function called value iteration. The key idea behind value iteration is to think of this identity as a set of constraints that tie together V*(s) at different states s∈S. We initialize the value function to some arbitrary values V0(s) for all states s∈S. At the kth iteration, the Value Iteration algorithm updates the value function as

동적 프로그래밍의 원리를 가치 반복이라는 최적의 가치 함수를 찾는 알고리즘으로 바꿀 수 있습니다. Value Iteration의 핵심 아이디어는 이 동일성을 서로 다른 상태 s∈S에서 V*(s)를 함께 묶는 제약 조건 집합으로 생각하는 것입니다. 우리는 모든 상태 s∈S에 대해 임의의 값 V0(s)로 가치 함수를 초기화합니다. k번째 반복에서 Value Iteration 알고리즘은 값 함수를 다음과 같이 업데이트합니다.

It turns out that as k→∞ the value function estimated by the Value Iteration algorithm converges to the optimal value function irrespective of the initialization V0,

Value Iteration 알고리즘에 의해 추정된 값 함수는 k → 마다 초기화 V0에 관계없이 최적의 값 함수로 수렴하는 것으로 나타났습니다.

The same Value Iteration algorithm can be equivalently written using the action-value function as

동일한 Value Iteration 알고리즘은 다음과 같이 action-value 함수를 사용하여 동등하게 작성할 수 있습니다.

In this case we initialize Q0(s,a) to some arbitrary values for all s∈S and a∈A. Again we have Q*(s,a)=lim k→∞ Qk(s,a) for all s∈S and a∈A.

이 경우 Q0(s,a)를 모든 s∈S 및 a∈A에 대한 임의의 값으로 초기화합니다. 다시 우리는 모든 s∈S 및 a∈A에 대해 Q*(s,a)=lim k→킵 Qk(s,a)를 갖습니다.

Value Iteration 이란?

"Value Iteration" is an iterative algorithm used in reinforcement learning and dynamic programming to find the optimal value function for a Markov decision process (MDP). It's a fundamental method for solving problems where an agent makes decisions in an uncertain environment over a sequence of discrete time steps.

'가치 반복(Value Iteration)'은 강화 학습과 동적 프로그래밍에서 사용되는 반복 알고리즘으로, 마르코프 결정 프로세스(MDP)에 대한 최적 가치 함수를 찾는 데 사용됩니다. 이 알고리즘은 에이전트가 불확실한 환경에서 일련의 이산 시간 단계 동안 결정을 내리는 문제를 해결하는 데 사용되는 기본적인 방법입니다.

Here's an overview of the key concepts related to Value Iteration:

가치 반복과 관련된 주요 개념을 살펴보겠습니다:

1. Markov Decision Process (MDP): Value Iteration is typically applied to problems modeled as MDPs. An MDP consists of a set of states, a set of actions, transition probabilities, rewards, and a discount factor. It's a mathematical framework used to represent decision-making problems under uncertainty.
   
   마르코프 결정 프로세스(MDP): 가치 반복은 일반적으로 MDP로 모델링된 문제에 적용됩니다. MDP는 상태 집합, 행동 집합, 전이 확률, 보상 및 할인 요소로 구성됩니다. 불확실성 하에서 의사 결정 문제를 표현하는 수학적 프레임워크입니다.
   
   
2. Value Function (V(s)): The goal of Value Iteration is to compute the value function V(s), which represents the expected cumulative rewards an agent can achieve starting from each state s while following an optimal policy. V(s) quantifies the desirability of being in a particular state.
   
   가치 함수(V(s)): 가치 반복의 목표는 각 상태 s에서 최적 정책을 따를 때 에이전트가 달성할 수 있는 기대 누적 보상을 나타내는 가치 함수 V(s)를 계산하는 것입니다. V(s)는 특정 상태에 머무르는 것의 바람직함을 측정합니다.
   
   
3. Bellman Equation: Value Iteration relies on the Bellman equation, which relates the value function of a state to the value functions of its neighboring states. The Bellman equation for state s is written as V(s) = max[R(s, a) + γ * Σ P(s' | s, a) * V(s')], where R(s, a) is the immediate reward of taking action a in state s, γ (gamma) is the discount factor, P(s' | s, a) is the transition probability to reach state s' from state s by taking action a, and V(s') is the value of state s'.
   
   벨만 방정식: 가치 반복은 상태의 가치 함수와 이웃 상태의 가치 함수 사이의 관계를 나타내는 벨만 방정식을 기반으로 합니다. 상태 s에 대한 벨만 방정식은 V(s) = max[R(s, a) + γ * Σ P(s' | s, a) * V(s')]로 표시되며, 여기서 R(s, a)는 상태 s에서 행동 a를 취했을 때 즉각적인 보상, γ(gamma)는 할인 요소, P(s' | s, a)는 행동 a를 취한 상태 s에서 상태 s'로 이동할 전이 확률, V(s')은 상태 s'의 가치를 나타냅니다.
   
   
4. Algorithm: Value Iteration starts with an initial estimate of the value function and iteratively updates it using the Bellman equation until it converges to the optimal value function. In each iteration, it computes the value for each state based on the current estimates of neighboring states' values. The process continues until the values no longer change significantly.
   
   알고리즘: 가치 반복은 가치 함수의 초기 추정치로 시작하여 벨만 방정식을 사용하여 상태의 값을 반복적으로 업데이트하고 최적 가치 함수에 수렴할 때까지 반복합니다. 각 반복에서는 현재 상태의 이웃 상태의 값을 기반으로 각 상태의 가치를 계산합니다. 가치가 더 이상 크게 변하지 않을 때까지 이 과정을 반복합니다.
   
   
5. Policy Extraction: Once the optimal value function is found, a corresponding optimal policy can be extracted by selecting actions that maximize the right-hand side of the Bellman equation for each state.
   
   정책 추출: 최적 가치 함수를 찾으면 각 상태에 대한 벨만 방정식 우변을 최대화하는 행동을 선택하여 해당하는 최적 정책을 추출할 수 있습니다.
   
   

Value Iteration is a powerful method for finding the optimal policy in MDPs, where the agent aims to maximize its expected cumulative rewards over time. It's known for its simplicity and efficiency, especially when the problem's state and action spaces are not too large. However, it might not be suitable for problems with very large state spaces due to the computational complexity of the algorithm.

가치 반복은 MDP에서 최적 정책을 찾는 강력한 방법으로, 에이전트가 시간이 지남에 따라 기대 누적 보상을 최대화하려는 경우에 사용됩니다. 특히 상태 및 행동 공간이 너무 크지 않은 경우에는 간단하고 효율적인 방법으로 알려져 있습니다. 그러나 상태 공간이 매우 큰 문제에는 알고리즘의 계산 복잡성 때문에 적합하지 않을 수 있습니다.

17.2.7. Policy Evaluation

Value Iteration enables us to compute the optimal value function, i.e., V**π* of the optimal deterministic policy π*. We can also use similar iterative updates to compute the value function associated with any other, potentially stochastic, policy π. We again initialize V0**π(s) to some arbitrary values for all states s∈S and at the kth iteration, perform the updates

Value Iteration을 사용하면 최적의 결정론적 정책 π*의 V**π*와 같은 최적의 가치 함수를 계산할 수 있습니다. 또한 유사한 반복 업데이트를 사용하여 잠재적으로 확률론적인 다른 정책 π와 관련된 가치 함수를 계산할 수도 있습니다. 모든 상태 s∈S에 대해 V0**π(s)를 임의의 값으로 다시 초기화하고 k번째 반복에서 업데이트를 수행합니다.

This algorithm is known as policy evaluation and is useful to compute the value function given the policy. Again, it turns out that as k→∞ these updates converge to the correct value function irrespective of the initialization V0,

이 알고리즘은 정책 평가로 알려져 있으며 정책에 따라 가치 함수를 계산하는 데 유용합니다. 다시 말하지만, k → π로 이러한 업데이트는 초기화 V0에 관계없이 올바른 값 함수로 수렴되는 것으로 나타났습니다.

The algorithm for computing the action-value function Q**π(s,a) of a policy π is analogous.

정책 π의 행동-가치 함수 Q**π(s,a)를 계산하는 알고리즘은 유사합니다.

Policy Evaluation이란?

"Policy Evaluation" is a fundamental step in the field of reinforcement learning, particularly in solving Markov decision processes (MDPs). It is the process of determining how good a given policy is by estimating the expected cumulative rewards an agent can achieve when following that policy in a given environment.

'정책 평가(Policy Evaluation)'는 강화 학습 분야에서 중요한 단계로, 특히 마르코프 결정 프로세스(MDP)를 해결하는 데 사용됩니다. 이는 주어진 환경에서 특정 정책을 따를 때 에이전트가 어떤 정책인지를 결정하는 과정입니다.

Here's a breakdown of what Policy Evaluation involves:

정책 평가가 포함하는 내용을 살펴보겠습니다:

1. Policy: A policy in reinforcement learning is a strategy that defines the agent's behavior in an environment. It specifies the mapping from states to actions, indicating what action to take in each state.
   
   정책: 강화 학습에서 정책은 환경에서 에이전트의 행동을 정의하는 전략입니다. 이는 상태에서 행동으로의 매핑을 지정하며, 각 상태에서 어떤 행동을 취할지를 나타냅니다.
   
   
2. Value Function: Policy Evaluation aims to compute the value function associated with a given policy. The value function, denoted as V(s), represents the expected cumulative rewards an agent can obtain when starting from a particular state s and following the specified policy.
   
   가치 함수: 정책 평가는 주어진 정책과 관련된 가치 함수를 계산하기 위한 과정입니다. 가치 함수는 V(s)로 표시되며, 특정 상태 s에서 시작하여 지정된 정책을 따를 때 에이전트가 얻을 수 있는 기대 누적 보상을 나타냅니다.
   
   
3. Bellman Expectation Equation: Policy Evaluation relies on the Bellman Expectation Equation, which expresses the value of a state in terms of the values of its neighboring states. It is typically represented as V(s) = R(s) + γ * Σ P(s' | s, π(s)) * V(s'), where R(s) is the immediate reward in state s, γ (gamma) is the discount factor, P(s' | s, π(s)) is the transition probability to reach state s' from state s by following the policy π(s), and V(s') is the value of state s'.
   
   벨만 기대 방정식: 정책 평가는 벨만 기대 방정식을 기반으로 합니다. 이 방정식은 상태의 가치를 해당 상태의 이웃 상태의 가치로 표현합니다. 일반적으로 V(s) = R(s) + γ * Σ P(s' | s, π(s)) * V(s')로 표현되며, 여기서 R(s)는 상태 s에서의 즉각적인 보상, γ (감소 요소)는 할인 요소, P(s' | s, π(s))는 정책 π(s)를 따라 상태 s에서 상태 s'로 이동할 전이 확률, V(s')은 상태 s'의 가치를 나타냅니다.
   
   
4. Iterative Process: Policy Evaluation is often an iterative process. It starts with an initial estimate of the value function and iteratively updates the values of states based on the Bellman Expectation Equation until the values converge or change very little between iterations.
   
   반복적인 프로세스: 정책 평가는 종종 반복적인 프로세스입니다. 초기 가치 함수의 추정치로 시작하고 벨만 기대 방정식을 기반으로 상태의 가치를 반복적으로 업데이트합니다. 값이 수렴하거나 반복 간에 값이 거의 변하지 않을 때까지 진행됩니다.
   
   
5. Convergence: Policy Evaluation continues until the value function estimates stabilize, meaning that further iterations do not significantly change the values. This indicates that the value function has converged to the true value function for the given policy.
   
   수렴: 정책 평가는 값 함수의 추정치가 안정화될 때까지 계속됩니다. 이는 값 함수의 추정치가 주어진 정책에 대한 실제 값 함수로 수렴했음을 나타냅니다.
   
   

Policy Evaluation serves as a crucial component in many reinforcement learning algorithms, such as Policy Iteration and Value Iteration, where it is used to assess and improve policies. By accurately estimating the value of each state under a policy, it helps the agent make informed decisions and find the optimal policy that maximizes the expected cumulative rewards in the environment.

정책 평가는 정책 평가를 평가하고 개선하는 데 사용되는 많은 강화 학습 알고리즘에서 중요한 구성 요소로 사용됩니다. 각 상태의 값을 정확하게 추정함으로써 에이전트는 정보에 기반하여 결정을 내리고 환경에서 기대 누적 보상을 최대화하는 최적 정책을 찾는 데 도움을 줍니다.

17.2.8. Implementation of Value Iteration

We next show how to implement Value Iteration for a navigation problem called FrozenLake from Open AI Gym. We first need to setup the enviroment as shown in the following code.

다음으로 Open AI Gym에서 FrozenLake라는 탐색 문제에 대한 Value Iteration을 구현하는 방법을 보여줍니다. 먼저 다음 코드와 같이 환경을 설정해야 합니다.

%matplotlib inline
import random
import numpy as np
from d2l import torch as d2l

seed = 0  # Random number generator seed
gamma = 0.95  # Discount factor
num_iters = 10  # Number of iterations
random.seed(seed)  # Set the random seed to ensure results can be reproduced
np.random.seed(seed)

# Now set up the environment
env_info = d2l.make_env('FrozenLake-v1', seed=seed)

이 코드는 강화 학습 문제를 설정하고 환경을 초기화하는 데 사용됩니다. 주요 내용을 설명하겠습니다.

1. %matplotlib inline: 이 라인은 주피터 노트북에서 그래프를 인라인으로 표시하도록 하는 명령입니다. 그래프나 시각화를 출력하려면 이 명령을 사용합니다.
2. import random: Python의 내장 라이브러리인 random을 임포트합니다. random 모듈은 난수 생성과 관련된 함수를 제공합니다.
3. import numpy as np: NumPy를 임포트하고 별칭인 np로 사용합니다. NumPy는 과학적 계산을 위한 파이썬 라이브러리로, 다차원 배열과 관련된 다양한 기능을 제공합니다.
4. from d2l import torch as d2l: d2l 라이브러리에서 torch 모듈을 가져와 d2l 별칭으로 사용합니다. 이 라이브러리는 "Dive into Deep Learning"의 예제 및 유틸리티 함수를 제공합니다.
5. seed = 0: 난수 생성기의 시드 값을 설정합니다. 시드는 난수 생성의 초기 상태를 결정하는 값으로, 동일한 시드를 사용하면 같은 난수가 생성됩니다. 따라서 결과를 재현할 수 있도록 시드를 설정합니다.
6. gamma = 0.95: 강화 학습에서 사용하는 할인 요소(discount factor)입니다. 할인 요소는 미래 보상을 현재 가치로 감소시키는 데 사용됩니다. 값이 0에서 1 사이의 실수입니다.
7. num_iters = 10: 강화 학습 알고리즘에서 수행할 반복 횟수 또는 에피소드 수를 설정합니다. 이 예에서는 10번의 반복을 수행합니다.
8. random.seed(seed): Python의 랜덤 시드를 설정하여 난수 생성을 초기화합니다. 이렇게 함으로써 동일한 시드를 사용하면 항상 같은 난수가 생성됩니다. 결과 재현성을 위해 시드를 설정합니다.
9. np.random.seed(seed): NumPy의 난수 생성기의 시드를 설정합니다. 이 역시 결과 재현성을 위한 조치입니다.
10. env_info = d2l.make_env('FrozenLake-v1', seed=seed): d2l 라이브러리의 make_env 함수를 사용하여 강화 학습 환경을 설정합니다. 여기서는 "FrozenLake-v1" 환경을 사용하며, 앞서 설정한 시드를 적용합니다. "FrozenLake"는 OpenAI Gym에서 제공하는 강화 학습 환경 중 하나로, 얼어붙은 호수를 건너는 에이전트를 제어하는 문제입니다.

이제 강화 학습 환경이 설정되었으며, 이를 사용하여 에이전트를 훈련하고 평가할 수 있게 됩니다.

In the FrozenLake environment, the robot moves on a 4×4 grid (these are the states) with actions that are “up” (↑), “down” (→), “left” (←), and “right” (→). The environment contains a number of holes (H) cells and frozen (F) cells as well as a goal cell (G), all of which are unknown to the robot. To keep the problem simple, we assume the robot has reliable actions, i.e. P(s′∣s,a)=1 for all s∈S,a∈A. If the robot reaches the goal, the trial ends and the robot receives a reward of 1 irrespective of the action; the reward at any other state is 0 for all actions. The objective of the robot is to learn a policy that reaches the goal location (G) from a given start location (S) (this is s0) to maximize the return.

FrozenLake 환경에서 로봇은 4X4 grid (이것이 state임)에서 "위"(↑), "아래"(→), "왼쪽"(←), "오른쪽"( →)의 action들에 의해 움직입니다.  환경에는 다수의 구멍(H) 세포와 동결(F) 세포 및 목표 세포(G)가 포함되어 있으며, 이들 모두는 로봇에 알려지지 않습니다. 문제를 단순하게 유지하기 위해 로봇이 신뢰할 수 있는 동작을 한다고 가정합니다. 즉, 모든 s∈S,a∈A에 대해 P(s′∣s,a)=1입니다. 로봇이 목표에 도달하면 시험이 종료되고 로봇은 행동에 관계없이 1의 보상을 받습니다. 다른 상태에서의 보상은 모든 행동에 대해 0입니다. 로봇의 목적은 주어진 시작 위치(S)(이것은 s0)에서 목표 위치(G)에 도달하는 정책을 학습하여 수익을 극대화하는 것입니다.

The following function implements Value Iteration, where env_info contains MDP and environment related information and gamma is the discount factor:

다음 함수는 Value Iteration을 구현합니다. 여기서 env_info에는 MDP 및 환경 관련 정보가 포함되고 감마는 할인 요소입니다.

def value_iteration(env_info, gamma, num_iters):
    env_desc = env_info['desc']  # 2D array shows what each item means
    prob_idx = env_info['trans_prob_idx']
    nextstate_idx = env_info['nextstate_idx']
    reward_idx = env_info['reward_idx']
    num_states = env_info['num_states']
    num_actions = env_info['num_actions']
    mdp = env_info['mdp']

    V  = np.zeros((num_iters + 1, num_states))
    Q  = np.zeros((num_iters + 1, num_states, num_actions))
    pi = np.zeros((num_iters + 1, num_states))

    for k in range(1, num_iters + 1):
        for s in range(num_states):
            for a in range(num_actions):
                # Calculate \sum_{s'} p(s'\mid s,a) [r + \gamma v_k(s')]
                for pxrds in mdp[(s,a)]:
                    # mdp(s,a): [(p1,next1,r1,d1),(p2,next2,r2,d2),..]
                    pr = pxrds[prob_idx]  # p(s'\mid s,a)
                    nextstate = pxrds[nextstate_idx]  # Next state
                    reward = pxrds[reward_idx]  # Reward
                    Q[k,s,a] += pr * (reward + gamma * V[k - 1, nextstate])
            # Record max value and max action
            V[k,s] = np.max(Q[k,s,:])
            pi[k,s] = np.argmax(Q[k,s,:])
    d2l.show_value_function_progress(env_desc, V[:-1], pi[:-1])

value_iteration(env_info=env_info, gamma=gamma, num_iters=num_iters)

이 코드는 가치 반복(Value Iteration) 알고리즘을 사용하여 강화 학습 환경에서 최적 가치 함수(Optimal Value Function)와 최적 정책(Optimal Policy)을 찾는 데 사용됩니다. 가치 반복은 동적 프로그래밍(Dynamic Programming) 기술 중 하나로, 최적 가치 함수를 업데이트하고 최적 정책을 추정하여 에이전트를 최적으로 학습시키는 방법입니다.

주요 내용을 설명하겠습니다.

1. env_desc, prob_idx, nextstate_idx, reward_idx, num_states, num_actions, mdp 등의 변수: 이 변수들은 강화 학습 환경 정보를 저장하는데 사용됩니다. 각 변수는 다음과 같은 역할을 합니다.
   • env_desc: 환경의 구조를 나타내는 2차원 배열로, 각 원소는 환경의 상태를 나타냅니다.
   • prob_idx, nextstate_idx, reward_idx: 강화 학습 환경의 상태 전이 확률, 다음 상태, 보상 정보의 인덱스를 나타냅니다.
   • num_states: 상태의 개수를 나타냅니다.
   • num_actions: 행동의 개수를 나타냅니다.
   • mdp: 환경의 확률적 상태 전이 정보를 나타내는 딕셔너리입니다.
2. V, Q, pi 변수: 이 변수들은 각각 가치 함수, 행동 가치 함수, 정책을 나타냅니다. 이러한 변수들은 반복적으로 업데이트되며, 최적 가치 함수와 최적 정책을 추정하는 데 사용됩니다.
3. for k in range(1, num_iters + 1):: 지정된 반복 횟수(num_iters) 동안 가치 반복 알고리즘을 실행합니다.
4. for s in range(num_states):: 모든 상태에 대해 반복합니다.
5. for a in range(num_actions):: 모든 가능한 행동에 대해 반복합니다.
6. for pxrds in mdp[(s,a)]:: 상태 전이 확률, 다음 상태, 보상, 종료 여부 정보를 mdp에서 가져와 반복합니다. 이 정보는 확률적 상태 전이를 나타냅니다.
7. pr, nextstate, reward: 상태 전이 확률, 다음 상태, 보상 값을 가져옵니다.
8. Q[k,s,a] += pr * (reward + gamma * V[k - 1, nextstate]): 행동 가치 함수 Q를 업데이트합니다. 이식은 벨만 방정식을 따릅니다.
9. V[k,s] = np.max(Q[k,s,:]): 가치 함수 V를 업데이트하고, 해당 상태에서 최대 가치를 기록합니다.
10. pi[k,s] = np.argmax(Q[k,s,:]): 정책을 업데이트하고, 해당 상태에서 최적 행동을 기록합니다.
11. d2l.show_value_function_progress(env_desc, V[:-1], pi[:-1]): 현재까지의 반복에서 얻은 최적 가치 함수와 최적 정책을 시각화하여 표시합니다.
12. value_iteration(env_info=env_info, gamma=gamma, num_iters=num_iters): 가치 반복 알고리즘을 실행하는 함수를 호출합니다.

이렇게 가치 반복 알고리즘은 주어진 환경에서 최적의 가치 함수와 최적의 정책을 찾아냅니다. 최적의 정책은 에이전트가 어떤 상태에서 어떤 행동을 선택해야 하는지를 결정합니다.

The above pictures show the policy (the arrow indicates the action) and value function (the change in color shows how the value function changes over time from the initial value shown by dark color to the optimal value shown by light colors.). As we see, Value Iteration finds the optimal value function after 10 iterations and the goal state (G) can be reached starting from any state as long as it is not an H cell. Another interesting aspect of the implementation is that in addition to finding the optimal value function, we also automatically found the optimal policy π* corresponding to this value function.

위 그림은 정책(화살표는 동작을 나타냄)과 가치함수(색상 변화는 가치함수가 시간에 따라 어두운 색으로 표시된 초기 값에서 밝은 색으로 표시된 최적의 값으로 어떻게 변화하는지 보여줍니다.)를 보여줍니다. 보시다시피 Value Iteration은 10번의 반복 후에 최적의 가치 함수를 찾고 목표 상태(G)는 H 셀이 아닌 한 어떤 상태에서도 도달할 수 있습니다. 구현의 또 다른 흥미로운 측면은 최적의 가치 함수를 찾는 것 외에도 이 가치 함수에 해당하는 최적의 정책 π*를 자동으로 찾았다는 것입니다.

17.2.9. Summary

The main idea behind the Value Iteration algorithm is to use the principle of dynamic programming to find the optimal average return obtained from a given state. Note that implementing the Value Iteration algorithm requires that we know the Markov decision process (MDP), e.g., the transition and reward functions, completely.

Value Iteration 알고리즘의 주요 아이디어는 동적 프로그래밍의 원리를 사용하여 주어진 상태에서 얻은 최적의 평균 수익을 찾는 것입니다. Value Iteration 알고리즘을 구현하려면 Markov 결정 프로세스(MDP), 예를 들어 전환 및 보상 기능을 완전히 알아야 합니다.

https://d2l.ai/chapter_reinforcement-learning/mdp.html

17.1. Markov Decision Process (MDP)

In this section, we will discuss how to formulate reinforcement learning problems using Markov decision processes (MDPs) and describe various components of MDPs in detail.

이 섹션에서는 MDP(Markov Decision Process)를 사용하여 강화학습 문제를 공식화하는 방법을 논의하고 MDP의 다양한 구성 요소를 자세히 설명합니다.

17.1.1. Definition of an MDP

A Markov decision process (MDP) (Bellman, 1957) is a model for how the state of a system evolves as different actions are applied to the system. A few different quantities come together to form an MDP.

마르코프 결정 프로세스(MDP)(Bellman, 1957)는 다양한 작업이 시스템에 적용될 때 시스템 상태가 어떻게 발전하는지에 대한 모델입니다. 몇 가지 다른 양이 모여서 MDP를 형성합니다.

• Let S be the set of states in the MDP. As a concrete example see Fig. 17.1.1, for a robot that is navigating a gridworld. In this case, S corresponds to the set of locations that the robot can be at any given timestep.
  
  S를 MDP의 상태 집합으로 설정합니다. 구체적인 예로 그리드 세계를 탐색하는 로봇에 대한 그림 17.1.1을 참조하세요. 이 경우 S는 주어진 시간 단계에서 로봇이 있을 수 있는 위치 집합에 해당합니다.
  
  
• Let A be the set of actions that the robot can take at each state, e.g., “go forward”, “turn right”, “turn left”, “stay at the same location”, etc. Actions can change the current state of the robot to some other state within the set S.
  
  A를 로봇이 각 상태에서 취할 수 있는 일련의 작업(예: "앞으로 이동", "우회전", "좌회전", "같은 위치에 유지" 등)이라고 가정합니다. 작업은 로봇의 현재 상태를 변경할 수 있습니다. 로봇을 세트 S 내의 다른 상태로 전환합니다.
  
  
• It may happen that we do not know how the robot moves exactly but only know it up to some approximation. We model this situation in reinforcement learning as follows: if the robot takes an action “go forward”, there might be a small probability that it stays at the current state, another small probability that it “turns left”, etc. Mathematically, this amounts to defining a “transition function” T:S×A×S→[0,1] such that T(s,a,s′)=P(s′∣s,a) using the conditional probability of reaching a state s′ given that the robot was at state s and took an action a. The transition function is a probability distribution and we therefore have ∑s′∈s**T(s,a,s′)=1 for all s∈S and a∈A, i.e., the robot has to go to some state if it takes an action.
  
  로봇이 정확히 어떻게 움직이는지는 모르지만 대략적인 정도까지만 알 수 있는 경우도 있습니다. 우리는 강화 학습에서 이 상황을 다음과 같이 모델링합니다. 로봇이 "앞으로 나아가는" 행동을 취하면 현재 상태에 머무를 확률이 작을 수도 있고 "좌회전"할 확률도 작을 수도 있습니다. 수학적으로 이는 상태에 도달할 조건부 확률을 사용하여 T(s,a,s')=P(s'∣s,a)가 되도록 "전이 함수" T:S×A×S→[0,1]을 정의하는 것과 같습니다. s' 로봇이 s 상태에 있고 조치를 취했다는 점을 고려하면 a. 전이 함수는 확률 분포이므로 모든 s∈S 및 a∈A에 대해 ∑s′∈s**T(s,a,s′)=1입니다. 즉, 로봇은 다음과 같은 경우 어떤 상태로 이동해야 합니다. 조치가 필요합니다.
  
  
• We now construct a notion of which actions are useful and which ones are not using the concept of a “reward” r:S×A→ℝ. We say that the robot gets a reward r(s,a) if the robot takes an action a at state s. If the reward r(s,a) is large, this indicates that taking the action a at state s is more useful to achieving the goal of the robot, i.e., going to the green house. If the reward r(s,a) is small, then action a is less useful to achieving this goal. It is important to note that the reward is designed by the user (the person who creates the reinforcement learning algorithm) with the goal in mind.
  
  이제 우리는 어떤 행동이 유용하고 어떤 행동이 "보상" r:S×A→ℝ 개념을 사용하지 않는지에 대한 개념을 구성합니다. 로봇이 상태 s에서 행동 a를 취하면 로봇은 보상 r(s,a)를 받는다고 말합니다. 보상 r(s,a)가 크다면, 이는 상태 s에서 a를 취하는 것이 로봇의 목표, 즉 온실로 가는 것을 달성하는 데 더 유용하다는 것을 나타냅니다. 보상 r(s,a)가 작으면 작업 a는 이 목표를 달성하는 데 덜 유용합니다. 보상은 목표를 염두에 두고 사용자(강화학습 알고리즘을 생성하는 사람)에 의해 설계된다는 점에 유의하는 것이 중요합니다.
  
  

17.1.2. Return and Discount Factor

The different components above together form a Markov decision process (MDP)

위의 다양한 구성 요소가 함께 MDP(Markov Decision Process)를 구성합니다.

Let’s now consider the situation when the robot starts at a particular state s0∈S and continues taking actions to result in a trajectory

이제 로봇이 특정 상태 s0∈S에서 시작하여 계속해서 궤적을 생성하는 작업을 수행하는 상황을 고려해 보겠습니다.

At each time step t the robot is at a state st and takes an action at which results in a reward rt=r(st,at). The return of a trajectory is the total reward obtained by the robot along such a trajectory

각 시간 단계 t에서 로봇은 상태 st에 있고 보상 rt=r(st,at)을 가져오는 작업을 수행합니다. 궤도의 복귀는 그러한 궤도를 따라 로봇이 얻는 총 보상입니다.

The goal in reinforcement learning is to find a trajectory that has the largest return.

강화학습의 목표는 가장 큰 수익을 내는 궤적을 찾는 것입니다.

Think of the situation when the robot continues to travel in the gridworld without ever reaching the goal location. The sequence of states and actions in a trajectory can be infinitely long in this case and the return of any such infinitely long trajectory will be infinite. In order to keep the reinforcement learning formulation meaningful even for such trajectories, we introduce the notion of a discount factor γ<1. We write the discounted return as

로봇이 목표 위치에 도달하지 못한 채 그리드 세계에서 계속 이동하는 상황을 생각해 보세요. 이 경우 궤도의 상태와 동작의 순서는 무한히 길어질 수 있으며 무한히 긴 궤도의 반환은 무한합니다. 그러한 궤적에 대해서도 강화 학습 공식을 의미 있게 유지하기 위해 할인 계수 γ<1이라는 개념을 도입합니다. 우리는 할인된 수익을 다음과 같이 씁니다.

Note that if γ is very small, the rewards earned by the robot in the far future, say t=1000, are heavily discounted by the factor γ**1000. This encourages the robot to select short trajectories that achieve its goal, namely that of going to the green house in the gridwold example (see Fig. 17.1.1). For large values of the discount factor, say γ=0.99, the robot is encouraged to explore and then find the best trajectory to go to the goal location.

γ가 매우 작은 경우, 먼 미래에 로봇이 얻는 보상(t=1000)은 γ**1000 인자로 크게 할인됩니다. 이는 로봇이 목표를 달성하는 짧은 궤적, 즉 그리드월드 예에서 온실로 가는 경로를 선택하도록 장려합니다(그림 17.1.1 참조). 할인 요소의 큰 값(γ=0.99라고 가정)의 경우 로봇은 목표 위치로 이동하기 위한 최적의 궤적을 탐색하고 찾도록 권장됩니다.

17.1.3. Discussion of the Markov Assumption

Let us think of a new robot where the state st is the location as above but the action at is the acceleration that the robot applies to its wheels instead of an abstract command like “go forward”. If this robot has some non-zero velocity at state st, then the next location st+1 is a function of the past location st, the acceleration at, also the velocity of the robot at time t which is proportional to st−st−1. This indicates that we should have

위와 같이 상태 st가 위치이지만 동작은 "전진"과 같은 추상적인 명령 대신 로봇이 바퀴에 적용하는 가속도인 새로운 로봇을 생각해 보겠습니다. 이 로봇이 상태 st에서 0이 아닌 속도를 갖는 경우 다음 위치 st+1은 과거 위치 st의 함수, 가속도, st−st−에 비례하는 시간 t에서의 로봇 속도의 함수입니다. 1. 이는 우리가 이것을 가져야 함을 나타냅니다.

the “some function” in our case would be Newton’s law of motion. This is quite different from our transition function that simply depends upon st and at.

우리의 경우 "some function"은 뉴턴의 운동 법칙이 될 것입니다. 이는 단순히 st와 at에 의존하는 전환 함수와는 상당히 다릅니다.

Markov systems are all systems where the next state st+1 is only a function of the current state st and the action αt taken at the current state. In Markov systems, the next state does not depend on which actions were taken in the past or the states that the robot was at in the past. For example, the new robot that has acceleration as the action above is not Markovian because the next location st+1 depends upon the previous state st−1 through the velocity. It may seem that Markovian nature of a system is a restrictive assumption, but it is not so. Markov Decision Processes are still capable of modeling a very large class of real systems. For example, for our new robot, if we chose our state st to the tuple (location,velocity) then the system is Markovian because its next state (location t+1,velocity t+1) depends only upon the current state (location t,velocity t) and the action at the current state αt.

마르코프 시스템은 다음 상태 st+1이 현재 상태 st와 현재 상태에서 취한 조치 αt의 함수일 뿐인 모든 시스템입니다. Markov 시스템에서 다음 상태는 과거에 어떤 작업이 수행되었는지 또는 로봇이 과거에 있었던 상태에 의존하지 않습니다. 예를 들어, 위의 동작으로 가속도를 갖는 새 로봇은 다음 위치 st+1이 속도를 통해 이전 상태 st-1에 의존하기 때문에 Markovian이 아닙니다. 시스템의 마코브적 특성은 제한적인 가정인 것처럼 보일 수 있지만 그렇지 않습니다. Markov 결정 프로세스는 여전히 매우 큰 규모의 실제 시스템을 모델링할 수 있습니다. 예를 들어, 새 로봇의 경우 상태 st를 튜플(위치, 속도)로 선택하면 다음 상태(위치 t+1, 속도 t+1)가 현재 상태(위치)에만 의존하기 때문에 시스템은 마코비안입니다. t,속도 t) 및 현재 상태에서의 작용 αt.

17.1.4. Summary

The reinforcement learning problem is typically modeled using Markov Decision Processes. A Markov decision process (MDP) is defined by a tuple of four entities (S,A,T,r) where S is the state space, A is the action space, T is the transition function that encodes the transition probabilities of the MDP and r is the immediate reward obtained by taking action at a particular state.

강화 학습 문제는 일반적으로 Markov 결정 프로세스를 사용하여 모델링됩니다. 마르코프 결정 프로세스(MDP)는 4개 엔터티(S,A,T,r)의 튜플로 정의됩니다. 여기서 S는 상태 공간, A는 작업 공간, T는 MDP의 전환 확률을 인코딩하는 전환 함수입니다. r은 특정 상태에서 조치를 취함으로써 얻은 즉각적인 보상입니다.

17.1.5. Exercises

1. Suppose that we want to design an MDP to model MountainCar problem.
   1. What would be the set of states?
   2. What would be the set of actions?
   3. What would be the possible reward functions?
2. How would you design an MDP for an Atari game like Pong game?

https://d2l.ai/chapter_reinforcement-learning/index.html

17. Reinforcement Learning

Pratik Chaudhari (University of Pennsylvania and Amazon), Rasool Fakoor (Amazon), and Kavosh Asadi (Amazon)

Reinforcement Learning (RL) is a suite of techniques that allows us to build machine learning systems that take decisions sequentially. For example, a package containing new clothes that you purchased from an online retailer arrives at your doorstep after a sequence of decisions, e.g., the retailer finding the clothes in the warehouse closest to your house, putting the clothes in a box, transporting the box via land or by air, and delivering it to your house within the city. There are many variables that affect the delivery of the package along the way, e.g., whether or not the clothes were available in the warehouse, how long it took to transport the box, whether it arrived in your city before the daily delivery truck left, etc. The key idea is that at each stage these variables that we do not often control affect the entire sequence of events in the future, e.g., if there were delays in packing the box in the warehouse the retailer may need to send the package via air instead of ground to ensure a timely delivery. Reinforcement Learning methods allow us to take the appropriate action at each stage of a sequential decision making problem in order to maximize some utility eventually, e.g., the timely delivery of the package to you.

강화 학습(RL)은 순차적으로 결정을 내리는 기계 학습 시스템을 구축할 수 있는 기술 모음입니다. 예를 들어, 온라인 소매점에서 구입한 새 옷이 들어 있는 패키지는 소매점이 집에서 가장 가까운 창고에서 옷을 찾고, 옷을 상자에 넣고, 상자를 운반하는 등 일련의 결정을 거쳐 문앞에 도착합니다. 육로나 항공으로 도시 내 집까지 배달해 드립니다. 도중에 패키지 배송에 영향을 미치는 많은 변수가 있습니다. 예를 들어 창고에 옷이 있는지 여부, 상자를 운송하는 데 걸리는 시간, 일일 배달 트럭이 떠나기 전에 상자가 도시에 도착했는지 여부 등이 있습니다. 핵심 아이디어는 각 단계에서 우리가 자주 제어하지 않는 이러한 변수가 미래의 전체 이벤트 순서에 영향을 미친다는 것입니다. 예를 들어, 창고에서 상자를 포장하는 데 지연이 발생한 경우 소매업체는 적시 배송을 보장하기 위해 육상 대신 항공을 통해 패키지를 보내야 할 수도 있습니다. 강화 학습 방법을 사용하면 궁극적으로 패키지를 적시에 전달하는 등 일부 유틸리티를 최대화하기 위해 순차적 의사 결정 문제의 각 단계에서 적절한 조치를 취할 수 있습니다.

Such sequential decision making problems are seen in numerous other places, e.g., while playing Go your current move determines the next moves and the opponent’s moves are the variables that you cannot control… a sequence of moves eventually determines whether or not you win; the movies that Netflix recommends to you now determine what you watch, whether you like the movie or not is unknown to Netflix, eventually a sequence of movie recommendations determines how satisfied you are with Netflix. Reinforcement learning is being used today to develop effective solutions to these problems (Mnih et al., 2013, Silver et al., 2016). The key distinction between reinforcement learning and standard deep learning is that in standard deep learning the prediction of a trained model on one test datum does not affect the predictions on a future test datum; in reinforcement learning decisions at future instants (in RL, decisions are also called actions) are affected by what decisions were made in the past.

이러한 순차적 의사 결정 문제는 다른 여러 곳에서 볼 수 있습니다. 예를 들어 바둑을 플레이하는 동안 현재 동작이 다음 동작을 결정하고 상대방의 동작은 제어할 수 없는 변수입니다. 일련의 동작이 결국 승리 여부를 결정합니다. 이제 Netflix가 추천하는 영화가 무엇을 시청할지 결정합니다. 영화를 좋아하는지 여부는 Netflix에 알려지지 않으며 결국 일련의 영화 추천에 따라 Netflix에 대한 만족도가 결정됩니다. 오늘날 강화 학습은 이러한 문제에 대한 효과적인 솔루션을 개발하는 데 사용되고 있습니다(Mnih et al., 2013, Silver et al., 2016). 강화 학습과 표준 딥 러닝의 주요 차이점은 표준 딥 러닝에서 하나의 테스트 데이터에 대한 훈련된 모델 예측이 향후 테스트 데이터에 대한 예측에 영향을 미치지 않는다는 것입니다. 강화 학습에서 미래 순간의 결정(RL에서는 결정이라고도 함)은 과거에 내려진 결정에 영향을 받습니다.

In this chapter, we will develop the fundamentals of reinforcement learning and obtain hands-on experience in implementing some popular reinforcement learning methods. We will first develop a concept called a Markov Decision Process (MDP) which allows us to think of such sequential decision making problems. An algorithm called Value Iteration will be our first insight into solving reinforcement learning problems under the assumption that we know how the uncontrolled variables in an MDP (in RL, these controlled variables are called the environment) typically behave. Using the more general version of Value Iteration, an algorithm called Q-Learning, we will be able to take appropriate actions even when we do not necessarily have full knowledge of the environment. We will then study how to use deep networks for reinforcement learning problems by imitating the actions of an expert. And finally, we will develop a reinforcement learning method that uses a deep network to take actions in unknown environments. These techniques form the basis of more advanced RL algorithms that are used today in a variety of real-world applications, some of which we will point to in the chapter.

이 장에서는 강화 학습의 기본 사항을 개발하고 몇 가지 널리 사용되는 강화 학습 방법을 구현하는 실습 경험을 얻을 것입니다. 우리는 먼저 이러한 순차적 의사결정 문제를 생각할 수 있게 해주는 Markov Decision Process(MDP)라는 개념을 개발할 것입니다. Value Iteration이라는 알고리즘은 MDP(RL에서는 이러한 제어 변수를 환경이라고 함)의 제어되지 않은 변수가 일반적으로 어떻게 동작하는지 알고 있다는 가정 하에 강화 학습 문제를 해결하기 위한 첫 번째 통찰력이 될 것입니다. Q-Learning이라는 알고리즘인 Value Iteration의 보다 일반적인 버전을 사용하면 환경에 대한 완전한 지식이 없어도 적절한 조치를 취할 수 있습니다. 그런 다음 전문가의 행동을 모방하여 강화 학습 문제에 딥 네트워크를 사용하는 방법을 연구합니다. 그리고 마지막으로 딥 네트워크를 활용하여 알려지지 않은 환경에서 조치를 취하는 강화학습 방법을 개발하겠습니다. 이러한 기술은 오늘날 다양한 실제 애플리케이션에서 사용되는 고급 RL 알고리즘의 기초를 형성하며, 그 중 일부는 이 장에서 언급할 것입니다.

Markov Decision Process(MDP)란?

'마르코프 결정 과정' 또는 'Markov Decision Process (MDP)'는 강화 학습(Reinforcement Learning)과 관련된 수학적 모델 및 프레임워크입니다. MDP는 시간 단계(time step)별로 에이전트가 환경과 상호 작용하는 상황을 수학적으로 모델링하는 데 사용됩니다.

MDP는 다음과 같은 구성 요소로 정의됩니다:

1. 상태(State): 에이전트가 존재하는 시스템의 현재 상태를 나타내는 값 또는 변수입니다. 이러한 상태는 모든 정보를 포함하며, 에이전트의 의사 결정에 영향을 미칩니다.
2. 행동(Action): 에이전트가 선택할 수 있는 가능한 행동 또는 행동의 집합입니다. 행동은 에이전트가 상태를 변경하거나 환경에 영향을 주는 방법입니다.
3. 보상(Reward): 각 상태에서 에이전트가 수행한 행동에 대한 즉각적인 피드백으로, 보상은 얼마나 좋은지 또는 나쁜지를 나타냅니다. 에이전트의 목표는 미래 보상의 합을 최대화하는 것입니다.
4. 상태 전이 확률(Transition Probability): 에이전트가 특정 상태에서 특정 행동을 선택할 때, 다음 상태로 이동할 확률을 나타냅니다. 이것은 환경의 동적인 특성을 모델링하는 데 사용됩니다.
5. 감쇠 계수(Discount Factor): 미래 보상의 현재 가치를 조절하는 매개변수로, 미래 보상에 대한 중요성을 나타냅니다.
6.  

MDP는 에이전트가 현재 상태에서 어떤 행동을 선택할지, 그 선택에 따른 보상을 최대화하기 위한 정책(Policy)을 학습하는 문제를 다룹니다. 최적의 정책은 최대 보상을 얻기 위한 행동 선택 전략입니다.

MDP는 강화 학습 문제를 정형화하고 수학적으로 해결 가능한 형태로 만들어주므로, 다양한 환경에서 에이전트의 학습과 의사 결정을 모델링하는 데 사용됩니다.

Reinforcement learning이란?

강화 학습(Reinforcement Learning)은 기계 학습의 한 분야로, 특정 환경 내에서 에이전트(Agent)가 어떤 일련의 행동을 수행하여 보상을 최대화하는 방법을 학습하는 프레임워크입니다. 이러한 환경은 주로 문제 해결에 관련되며, 강화 학습 에이전트는 환경과 상호작용하면서 다양한 상황에서 어떤 행동을 선택해야 하는지를 학습합니다.

강화 학습의 주요 구성 요소는 다음과 같습니다:

1. 에이전트(Agent): 학습하는 주체로, 의사 결정을 내리고 행동을 수행합니다. 이 에이전트는 주어진 상황에서 보상을 최대화하기 위한 최적의 행동을 찾아내는 것이 목표입니다.
2. 환경(Environment): 에이전트가 상호작용하는 대상으로, 문제의 성격에 따라 다양한 형태를 가질 수 있습니다. 환경은 에이전트의 행동에 따라 변화하며, 행동에 대한 응답으로 보상을 제공합니다.
3. 상태(State): 환경의 특정 순간 상태를 나타내는 정보입니다. 에이전트는 주어진 상태에서 어떤 행동을 선택해야 하는지 결정합니다.
4. 행동(Action): 에이전트가 환경에서 수행하는 행동 또는 의사 결정을 나타냅니다. 각 상태에서 가능한 행동의 집합이 정의되며, 에이전트는 이 중에서 하나를 선택합니다.
5. 보상(Reward): 에이전트의 행동에 대한 피드백으로, 주어진 행동이 얼마나 좋은지 또는 나쁜지를 나타냅니다. 목표는 보상을 최대화하는 행동을 선택하는 것입니다.

강화 학습의 핵심 과제는 에이전트가 주어진 환경에서 최적의 정책(Policy)을 학습하는 것입니다. 정책은 상태에 따라 에이전트가 어떤 행동을 선택해야 하는지를 결정하는 전략을 의미합니다. 에이전트는 다양한 정책을 시도하고 보상을 통해 피드백을 받으며 점차적으로 최적의 정책을 발견합니다.

강화 학습은 로봇 제어, 게임 플레이, 자율 주행 자동차, 자연어 처리 및 금융 등 다양한 응용 분야에서 사용됩니다. 주어진 환경에서 최적의 행동을 결정하는 방법을 학습함으로써 문제를 해결하는 데 활용됩니다.

16.7. Natural Language Inference: Fine-Tuning BERT — Dive into Deep Learning 1.0.3 documentation (d2l.ai)

16.7. Natural Language Inference: Fine-Tuning BERT

In earlier sections of this chapter, we have designed an attention-based architecture (in Section 16.5) for the natural language inference task on the SNLI dataset (as described in Section 16.4). Now we revisit this task by fine-tuning BERT. As discussed in Section 16.6, natural language inference is a sequence-level text pair classification problem, and fine-tuning BERT only requires an additional MLP-based architecture, as illustrated in Fig. 16.7.1.

이 장의 이전 섹션에서 우리는 SNLI 데이터 세트(섹션 16.4에서 설명)에 대한 자연어 추론 작업을 위한 attention-based architecture(섹션 16.5)를 설계했습니다. 이제 BERT를 미세 조정하여 이 작업을 다시 살펴보겠습니다. 섹션 16.6에서 설명한 것처럼 자연어 추론은 시퀀스 수준 텍스트 쌍 분류 문제이며 BERT를 미세 조정하려면 그림 16.7.1에 설명된 것처럼 추가적인 MLP 기반 아키텍처만 필요합니다.

In this section, we will download a pretrained small version of BERT, then fine-tune it for natural language inference on the SNLI dataset.

이 섹션에서는 사전 훈련된 BERT의 작은 버전을 다운로드한 다음 SNLI 데이터 세트에 대한 자연어 추론을 위해 미세 조정합니다.

import json
import multiprocessing
import os
import torch
from torch import nn
from d2l import torch as d2l

16.7.1. Loading Pretrained BERT

We have explained how to pretrain BERT on the WikiText-2 dataset in Section 15.9 and Section 15.10 (note that the original BERT model is pretrained on much bigger corpora). As discussed in Section 15.10, the original BERT model has hundreds of millions of parameters. In the following, we provide two versions of pretrained BERT: “bert.base” is about as big as the original BERT base model that requires a lot of computational resources to fine-tune, while “bert.small” is a small version to facilitate demonstration.

d2l.DATA_HUB['bert.base'] = (d2l.DATA_URL + 'bert.base.torch.zip',
                             '225d66f04cae318b841a13d32af3acc165f253ac')
d2l.DATA_HUB['bert.small'] = (d2l.DATA_URL + 'bert.small.torch.zip',
                              'c72329e68a732bef0452e4b96a1c341c8910f81f')

이 코드는 데이터 저장소(DATA_HUB)에 두 개의 BERT(Bidirectional Encoder Representations from Transformers) 모델에 대한 정보를 추가하는 역할을 합니다. BERT는 자연어 처리 작업에 사용되는 사전 훈련된 언어 모델 중 하나로, 큰 텍스트 코퍼스에서 학습된 후 다양한 NLP 작업에 전이 학습(transfer learning)을 적용할 수 있도록 훈련된 모델입니다.

• 'bert.base': 이 키는 큰 규모의 BERT 모델에 대한 정보를 나타냅니다. 해당 모델의 체크포인트 파일은 bert.base.torch.zip로 저장되어 있으며, 해당 파일을 다운로드하여 모델을 로드할 수 있습니다. 이 모델은 큰 언어 모델이기 때문에 자연어 처리 작업에 높은 성능을 제공할 것으로 기대됩니다.
• 'bert.small': 이 키는 작은 규모의 BERT 모델에 대한 정보를 나타냅니다. 작은 모델은 더 가벼우며 계산 비용이 적게 들지만, 큰 모델보다는 성능이 낮을 수 있습니다. 이 모델은 자연어 처리 작업에 적합한 자원이 제한된 환경에서 사용될 수 있습니다.

따라서 이 코드는 데이터 저장소에서 BERT 모델의 체크포인트 파일을 다운로드하고 이를 사용하여 BERT 모델을 로드할 수 있도록 필요한 정보를 설정합니다.

Either pretrained BERT model contains a “vocab.json” file that defines the vocabulary set and a “pretrained.params” file of the pretrained parameters. We implement the following load_pretrained_model function to load pretrained BERT parameters.

사전 훈련된 BERT 모델에는 어휘 세트를 정의하는 "vocab.json" 파일과 사전 훈련된 매개변수의 "pretrained.params" 파일이 포함되어 있습니다. 사전 훈련된 BERT 매개변수를 로드하기 위해 다음 load_pretrained_model 함수를 구현합니다.

def load_pretrained_model(pretrained_model, num_hiddens, ffn_num_hiddens,
                          num_heads, num_blks, dropout, max_len, devices):
    data_dir = d2l.download_extract(pretrained_model)
    # Define an empty vocabulary to load the predefined vocabulary
    vocab = d2l.Vocab()
    vocab.idx_to_token = json.load(open(os.path.join(data_dir, 'vocab.json')))
    vocab.token_to_idx = {token: idx for idx, token in enumerate(
        vocab.idx_to_token)}
    bert = d2l.BERTModel(
        len(vocab), num_hiddens, ffn_num_hiddens=ffn_num_hiddens, num_heads=4,
        num_blks=2, dropout=0.2, max_len=max_len)
    # Load pretrained BERT parameters
    bert.load_state_dict(torch.load(os.path.join(data_dir,
                                                 'pretrained.params')))
    return bert, vocab

이 함수는 다음과 같은 역할을 합니다:

1. pretrained_model: 미리 학습된 BERT 모델의 이름 또는 경로를 나타냅니다.
2. num_hiddens: BERT 모델의 은닉 상태 크기를 나타냅니다.
3. ffn_num_hiddens: BERT 모델의 Feedforward 네트워크에서의 은닉 상태 크기를 나타냅니다.
4. num_heads: BERT 모델의 어텐션 헤드 개수를 나타냅니다.
5. num_blks: BERT 모델의 어텐션 블록 수를 나타냅니다.
6. dropout: 드롭아웃 비율을 나타냅니다.
7. max_len: 입력 시퀀스의 최대 길이를 나타냅니다.
8. devices: 사용할 디바이스 목록입니다.

함수는 다음 단계로 수행됩니다:

• pretrained_model을 통해 지정된 미리 학습된 BERT 모델을 다운로드하고 압축을 해제합니다.
• 빈 어휘 사전(vocab)을 정의하고, 미리 정의된 어휘 파일을 로드하여 이 어휘 사전을 채웁니다.
• BERT 모델을 지정된 구성 및 어휘 사전을 사용하여 초기화합니다.
• 미리 학습된 BERT 모델의 파라미터를 로드하여 BERT 모델을 미리 학습된 상태로 설정합니다.
• 초기화된 BERT 모델과 어휘 사전을 반환합니다.

이 함수를 호출하면 미리 학습된 BERT 모델과 해당 어휘 사전이 반환됩니다. 이 모델을 사용하여 다양한 자연어 처리 작업을 수행할 수 있습니다.

To facilitate demonstration on most of machines, we will load and fine-tune the small version (“bert.small”) of the pretrained BERT in this section. In the exercise, we will show how to fine-tune the much larger “bert.base” to significantly improve the testing accuracy.

대부분의 머신에서 시연을 용이하게 하기 위해 이 섹션에서는 사전 훈련된 BERT의 작은 버전("bert.small")을 로드하고 미세 조정합니다. 이 연습에서는 훨씬 더 큰 "bert.base"를 미세 조정하여 테스트 정확도를 크게 향상시키는 방법을 보여줍니다.

devices = d2l.try_all_gpus()
bert, vocab = load_pretrained_model(
    'bert.small', num_hiddens=256, ffn_num_hiddens=512, num_heads=4,
    num_blks=2, dropout=0.1, max_len=512, devices=devices)

위의 코드는 BERT 모델을 불러오고 설정하는 작업을 수행합니다. 

1. devices = d2l.try_all_gpus(): 이 코드는 가능한 모든 GPU 디바이스를 사용 가능한 경우 가져옵니다. 이것은 여러 GPU에서 BERT 모델을 병렬로 학습하거나 추론할 때 사용됩니다.
2. load_pretrained_model(...): 이 함수는 앞서 정의한 load_pretrained_model 함수를 호출하여 미리 학습된 BERT 모델을 로드하고 설정합니다.
   • 'bert.small': 불러올 미리 학습된 BERT 모델의 이름 또는 경로를 나타냅니다.
   • num_hiddens=256: BERT 모델의 은닉 상태 크기를 설정합니다.
   • ffn_num_hiddens=512: BERT 모델의 Feedforward 네트워크에서의 은닉 상태 크기를 설정합니다.
   • num_heads=4: BERT 모델의 어텐션 헤드 개수를 설정합니다.
   • num_blks=2: BERT 모델의 어텐션 블록 수를 설정합니다.
   • dropout=0.1: 드롭아웃 비율을 설정합니다.
   • max_len=512: 입력 시퀀스의 최대 길이를 설정합니다.
   • devices=devices: 사용할 GPU 디바이스 목록을 전달합니다.

이 코드를 실행하면 bert 변수에는 설정된 BERT 모델이 로드되며, vocab 변수에는 어휘 사전이 로드됩니다. 이제 bert 모델을 사용하여 다양한 자연어 처리 작업을 수행할 수 있습니다.

Downloading ../data/bert.small.torch.zip from http://d2l-data.s3-accelerate.amazonaws.com/bert.small.torch.zip...

16.7.2. The Dataset for Fine-Tuning BERT

For the downstream task natural language inference on the SNLI dataset, we define a customized dataset class SNLIBERTDataset. In each example, the premise and hypothesis form a pair of text sequence and is packed into one BERT input sequence as depicted in Fig. 16.6.2. Recall Section 15.8.4 that segment IDs are used to distinguish the premise and the hypothesis in a BERT input sequence. With the predefined maximum length of a BERT input sequence (max_len), the last token of the longer of the input text pair keeps getting removed until max_len is met. To accelerate generation of the SNLI dataset for fine-tuning BERT, we use 4 worker processes to generate training or testing examples in parallel.

SNLI 데이터 세트에 대한 다운스트림 작업 자연어 추론을 위해 맞춤형 데이터 세트 클래스 SNLIBERTDataset를 정의합니다. 각 예에서 전제와 가설은 한 쌍의 텍스트 시퀀스를 형성하고 그림 16.6.2에 설명된 대로 하나의 BERT 입력 시퀀스로 압축됩니다. BERT 입력 시퀀스에서 전제와 가설을 구별하기 위해 세그먼트 ID가 사용된다는 섹션 15.8.4를 상기하세요. BERT 입력 시퀀스의 사전 정의된 최대 길이(max_len)를 사용하면 max_len이 충족될 때까지 더 긴 입력 텍스트 쌍의 마지막 토큰이 계속 제거됩니다. BERT 미세 조정을 위한 SNLI 데이터 세트 생성을 가속화하기 위해 4개의 작업자 프로세스를 사용하여 훈련 또는 테스트 예제를 병렬로 생성합니다.

class SNLIBERTDataset(torch.utils.data.Dataset):
    def __init__(self, dataset, max_len, vocab=None):
        all_premise_hypothesis_tokens = [[
            p_tokens, h_tokens] for p_tokens, h_tokens in zip(
            *[d2l.tokenize([s.lower() for s in sentences])
              for sentences in dataset[:2]])]

        self.labels = torch.tensor(dataset[2])
        self.vocab = vocab
        self.max_len = max_len
        (self.all_token_ids, self.all_segments,
         self.valid_lens) = self._preprocess(all_premise_hypothesis_tokens)
        print('read ' + str(len(self.all_token_ids)) + ' examples')

    def _preprocess(self, all_premise_hypothesis_tokens):
        pool = multiprocessing.Pool(4)  # Use 4 worker processes
        out = pool.map(self._mp_worker, all_premise_hypothesis_tokens)
        all_token_ids = [
            token_ids for token_ids, segments, valid_len in out]
        all_segments = [segments for token_ids, segments, valid_len in out]
        valid_lens = [valid_len for token_ids, segments, valid_len in out]
        return (torch.tensor(all_token_ids, dtype=torch.long),
                torch.tensor(all_segments, dtype=torch.long),
                torch.tensor(valid_lens))

    def _mp_worker(self, premise_hypothesis_tokens):
        p_tokens, h_tokens = premise_hypothesis_tokens
        self._truncate_pair_of_tokens(p_tokens, h_tokens)
        tokens, segments = d2l.get_tokens_and_segments(p_tokens, h_tokens)
        token_ids = self.vocab[tokens] + [self.vocab['<pad>']] \
                             * (self.max_len - len(tokens))
        segments = segments + [0] * (self.max_len - len(segments))
        valid_len = len(tokens)
        return token_ids, segments, valid_len

    def _truncate_pair_of_tokens(self, p_tokens, h_tokens):
        # Reserve slots for '<CLS>', '<SEP>', and '<SEP>' tokens for the BERT
        # input
        while len(p_tokens) + len(h_tokens) > self.max_len - 3:
            if len(p_tokens) > len(h_tokens):
                p_tokens.pop()
            else:
                h_tokens.pop()

    def __getitem__(self, idx):
        return (self.all_token_ids[idx], self.all_segments[idx],
                self.valid_lens[idx]), self.labels[idx]

    def __len__(self):
        return len(self.all_token_ids)

이 코드는 SNLI 데이터셋을 BERT 모델의 입력 형식에 맞게 전처리하는 데 사용되는 SNLIBERTDataset 클래스를 정의합니다. 이 클래스는 PyTorch의 torch.utils.data.Dataset 클래스를 상속하며, 데이터를 로드하고 전처리하는 역할을 합니다. 

1. __init__(self, dataset, max_len, vocab=None): 이 클래스의 생성자는 다음과 같은 매개변수를 받습니다.
   • dataset: SNLI 데이터셋.
   • max_len: BERT 입력 시퀀스의 최대 길이.
   • vocab: 어휘 사전 (생략 가능).
2. _preprocess(self, all_premise_hypothesis_tokens): 이 메서드는 데이터셋을 전처리하고 BERT 모델 입력에 맞게 변환합니다. 멀티프로세스를 사용하여 병렬로 처리하며, BERT 모델에 입력으로 들어갈 토큰 ID, 세그먼트 ID, 유효한 길이를 반환합니다.
3. _mp_worker(self, premise_hypothesis_tokens): 이 메서드는 멀티프로세스 작업을 위해 호출되며, 입력으로 주어진 전제와 가설 문장의 토큰을 BERT 입력 형식에 맞게 전처리합니다.
4. _truncate_pair_of_tokens(self, p_tokens, h_tokens): 이 메서드는 전제와 가설 문장의 토큰 길이가 max_len을 초과하지 않도록 자르는 역할을 합니다.
5. __getitem__(self, idx): 이 메서드는 데이터셋에서 특정 인덱스 idx에 해당하는 데이터를 반환합니다. 이 데이터는 BERT 모델의 입력과 레이블을 포함합니다.
6. __len__(self): 이 메서드는 데이터셋의 총 데이터 수를 반환합니다.

이 클래스를 사용하면 SNLI 데이터를 BERT 모델에 입력으로 제공하기 위한 데이터셋을 쉽게 생성할 수 있습니다.

After downloading the SNLI dataset, we generate training and testing examples by instantiating the SNLIBERTDataset class. Such examples will be read in minibatches during training and testing of natural language inference.

SNLI 데이터 세트를 다운로드한 후 SNLIBERTDataset 클래스를 인스턴스화하여 훈련 및 테스트 예제를 생성합니다. 이러한 예제는 자연어 추론을 훈련하고 테스트하는 동안 미니배치로 읽혀집니다.

# Reduce `batch_size` if there is an out of memory error. In the original BERT
# model, `max_len` = 512
batch_size, max_len, num_workers = 512, 128, d2l.get_dataloader_workers()
data_dir = d2l.download_extract('SNLI')
train_set = SNLIBERTDataset(d2l.read_snli(data_dir, True), max_len, vocab)
test_set = SNLIBERTDataset(d2l.read_snli(data_dir, False), max_len, vocab)
train_iter = torch.utils.data.DataLoader(train_set, batch_size, shuffle=True,
                                   num_workers=num_workers)
test_iter = torch.utils.data.DataLoader(test_set, batch_size,
                                  num_workers=num_workers)

이 코드는 BERT 모델을 사용하여 SNLI 데이터셋을 학습하기 위한 데이터 로딩 및 전처리 부분을 담당합니다.

1. batch_size, max_len, num_workers 설정: 이 부분에서는 배치 크기(batch_size), 최대 시퀀스 길이(max_len), 그리고 데이터 로더에 사용할 워커 수(num_workers)를 설정합니다. 원래 BERT 모델에서는 max_len을 512로 사용하나, 메모리 부족 문제가 발생할 경우 이 값을 낮출 수 있습니다.
2. 데이터 다운로드 및 전처리: data_dir 변수에 SNLI 데이터셋을 다운로드하고 압축을 해제합니다. 그 후, train_set과 test_set을 각각 SNLIBERTDataset 클래스로 초기화합니다. 이 때, max_len은 지정한 값으로 설정하고, vocab은 미리 로드한 어휘 사전을 사용합니다.
3. 데이터 로더 생성: train_set과 test_set을 기반으로 데이터 로더(train_iter와 test_iter)를 생성합니다. 데이터 로더는 미니배치를 생성하고 데이터를 셔플하며, 병렬로 데이터를 로드하기 위해 num_workers를 사용합니다.

이렇게 설정된 데이터 로더를 사용하여 BERT 모델을 학습하고 평가할 수 있습니다.

read 549367 examples
read 9824 examples

16.7.3. Fine-Tuning BERT

As Fig. 16.6.2 indicates, fine-tuning BERT for natural language inference requires only an extra MLP consisting of two fully connected layers (see self.hidden and self.output in the following BERTClassifier class). This MLP transforms the BERT representation of the special “<cls>” token, which encodes the information of both the premise and the hypothesis, into three outputs of natural language inference: entailment, contradiction, and neutral.

그림 16.6.2에서 알 수 있듯이 자연어 추론을 위해 BERT를 미세 조정하려면 두 개의 완전히 연결된 레이어로 구성된 추가 MLP만 필요합니다(다음 BERTClassifier 클래스의 self.hidden 및 self.output 참조). 이 MLP는 전제와 가설 모두의 정보를 인코딩하는 특수 "<cls>" 토큰의 BERT 표현을 수반, 모순 및 중립의 세 가지 자연어 추론 출력으로 변환합니다.

class BERTClassifier(nn.Module):
    def __init__(self, bert):
        super(BERTClassifier, self).__init__()
        self.encoder = bert.encoder
        self.hidden = bert.hidden
        self.output = nn.LazyLinear(3)

    def forward(self, inputs):
        tokens_X, segments_X, valid_lens_x = inputs
        encoded_X = self.encoder(tokens_X, segments_X, valid_lens_x)
        return self.output(self.hidden(encoded_X[:, 0, :]))

이 모델은 다음과 같은 구조를 가집니다:

1. self.encoder: BERT 모델의 인코더 부분을 가져와서 저장합니다. 이는 입력 데이터에 대한 특성 추출을 담당합니다.
2. self.hidden: BERT 모델의 은닉 상태 부분을 가져와서 저장합니다. 이 부분은 모델의 내부 표현을 다룹니다.
3. self.output: 감정 분류를 위한 출력 레이어로, 3개의 클래스로 분류하기 위한 선형 레이어입니다.

forward 메서드에서는 다음과 같은 과정을 거칩니다:

1. 입력 데이터(inputs)를 받습니다. 이 입력 데이터는 토큰, 세그먼트, 유효한 길이로 이루어져 있습니다.
2. 입력 데이터를 BERT 인코더(self.encoder)를 통해 처리하여 인코딩된 데이터(encoded_X)를 얻습니다.
3. 인코딩된 데이터 중 첫 번째 토큰(encoded_X[:, 0, :])의 표현을 가져와서 이를 출력 레이어(self.output)에 입력합니다.
4. 출력 레이어는 입력 표현을 활용하여 감정 분류를 수행하고 결과를 반환합니다.

이렇게 정의된 BERTClassifier 모델은 BERT를 기반으로 하여 텍스트 감정 분류를 수행하는 모델입니다.

In the following, the pretrained BERT model bert is fed into the BERTClassifier instance net for the downstream application. In common implementations of BERT fine-tuning, only the parameters of the output layer of the additional MLP (net.output) will be learned from scratch. All the parameters of the pretrained BERT encoder (net.encoder) and the hidden layer of the additional MLP (net.hidden) will be fine-tuned.

다음에서는 사전 훈련된 BERT 모델 bert가 다운스트림 애플리케이션을 위한 BERTClassifier 인스턴스 net에 공급됩니다. BERT 미세 조정의 일반적인 구현에서는 추가 MLP(net.output)의 출력 레이어 매개변수만 처음부터 학습됩니다. 사전 훈련된 BERT 인코더(net.encoder)의 모든 매개변수와 추가 MLP(net.hidden)의 숨겨진 계층이 미세 조정됩니다.

net = BERTClassifier(bert)

이 코드는 앞서 정의한 BERTClassifier 클래스를 사용하여 실제 BERT 모델을 텍스트 감정 분류를 위한 모델로 초기화하는 부분입니다.

여기서 net은 BERTClassifier 클래스의 인스턴스로, bert는 미리 학습된 BERT 모델을 의미합니다. 이 코드를 실행하면 net은 텍스트 감정 분류를 위한 모델로 설정되며, 이 모델은 BERT의 인코더와 은닉 상태를 활용하여 입력된 텍스트 데이터를 분류합니다.

즉, net을 사용하면 미리 학습된 BERT 모델을 감정 분류 작업에 활용할 수 있게 됩니다.

Recall that in Section 15.8 both the MaskLM class and the NextSentencePred class have parameters in their employed MLPs. These parameters are part of those in the pretrained BERT model bert, and thus part of parameters in net. However, such parameters are only for computing the masked language modeling loss and the next sentence prediction loss during pretraining. These two loss functions are irrelevant to fine-tuning downstream applications, thus the parameters of the employed MLPs in MaskLM and NextSentencePred are not updated (staled) when BERT is fine-tuned.

섹션 15.8에서 MaskLM 클래스와 NextSentencePred 클래스 모두 사용된 MLP에 매개변수를 가지고 있다는 점을 기억하세요. 이러한 매개변수는 사전 훈련된 BERT 모델 bert의 매개변수의 일부이므로 net의 매개변수의 일부입니다. 그러나 이러한 매개변수는 사전 훈련 중 마스크된 언어 모델링 손실과 다음 문장 예측 손실을 계산하는 데만 사용됩니다. 이 두 가지 손실 함수는 다운스트림 애플리케이션을 미세 조정하는 것과 관련이 없으므로 BERT가 미세 조정될 때 MaskLM 및 NextSentencePred에 사용된 MLP의 매개변수가 업데이트(정지)되지 않습니다.

To allow parameters with stale gradients, the flag ignore_stale_grad=True is set in the step function of d2l.train_batch_ch13. We use this function to train and evaluate the model net using the training set (train_iter) and the testing set (test_iter) of SNLI. Due to the limited computational resources, the training and testing accuracy can be further improved: we leave its discussions in the exercises.

오래된 그래디언트가 있는 매개변수를 허용하려면 d2l.train_batch_ch13의 단계 함수에ignore_stale_grad=True 플래그가 설정됩니다. 우리는 이 함수를 사용하여 SNLI의 훈련 세트(train_iter)와 테스트 세트(test_iter)를 사용하여 모델 네트워크를 훈련하고 평가합니다. 제한된 계산 리소스로 인해 훈련 및 테스트 정확도가 더욱 향상될 수 있습니다. 이에 대한 논의는 연습에 남겨두겠습니다.

lr, num_epochs = 1e-4, 5
trainer = torch.optim.Adam(net.parameters(), lr=lr)
loss = nn.CrossEntropyLoss(reduction='none')
net(next(iter(train_iter))[0])
d2l.train_ch13(net, train_iter, test_iter, loss, trainer, num_epochs, devices)

이 코드는 BERT 모델을 텍스트 감정 분류 작업에 학습시키는 부분입니다.

1. lr, num_epochs 변수는 학습률 (lr)과 학습 에포크 수 (num_epochs)를 설정합니다. lr은 0.0001로 설정되어 있으며, 학습률은 모델 가중치 업데이트에 사용되는 값입니다. num_epochs는 5로 설정되어 있으며, 데이터셋을 5번 반복하여 학습합니다.
2. trainer 변수는 torch.optim.Adam 옵티마이저를 초기화합니다. 이 옵티마이저는 모델의 파라미터를 업데이트하는 데 사용됩니다.
3. loss 변수는 nn.CrossEntropyLoss를 초기화합니다. 이 손실 함수는 다중 클래스 분류 작업에서 사용되며, 모델의 출력과 실제 레이블 간의 크로스 엔트로피 손실을 계산합니다. reduction='none'으로 설정되어 있으므로 손실을 각 샘플에 대한 개별 손실로 계산합니다.
4. net(next(iter(train_iter))[0]) 코드는 학습 데이터의 첫 번째 미니배치를 사용하여 모델을 실행하고 출력을 확인하는 용도로 사용됩니다.
5. d2l.train_ch13 함수를 호출하여 모델을 학습합니다. 이 함수는 모델, 학습 데이터 반복자, 테스트 데이터 반복자, 손실 함수, 옵티마이저, 학습 에포크 수, 그리고 디바이스를 입력으로 받아 모델을 학습하고 학습 결과를 시각화합니다. 이를 통해 BERT 모델이 텍스트 감정 분류 작업을 수행하도록 학습됩니다.

이러한 단계를 통해 BERT 모델이 주어진 데이터에 대해 감정 분류 작업을 수행하도록 학습됩니다.

loss 0.520, train acc 0.791, test acc 0.786
10588.8 examples/sec on [device(type='cuda', index=0), device(type='cuda', index=1)]

16.7.4. Summary

• We can fine-tune the pretrained BERT model for downstream applications, such as natural language inference on the SNLI dataset.
• SNLI 데이터세트에 대한 자연어 추론과 같은 다운스트림 애플리케이션을 위해 사전 훈련된 BERT 모델을 미세 조정할 수 있습니다.
• During fine-tuning, the BERT model becomes part of the model for the downstream application. Parameters that are only related to pretraining loss will not be updated during fine-tuning.
• 미세 조정 중에 BERT 모델은 다운스트림 애플리케이션을 위한 모델의 일부가 됩니다. 사전 훈련 손실에만 관련된 매개변수는 미세 조정 중에 업데이트되지 않습니다.

16.7.5. Exercises

1. Fine-tune a much larger pretrained BERT model that is about as big as the original BERT base model if your computational resource allows. Set arguments in the load_pretrained_model function as: replacing ‘bert.small’ with ‘bert.base’, increasing values of num_hiddens=256, ffn_num_hiddens=512, num_heads=4, and num_blks=2 to 768, 3072, 12, and 12, respectively. By increasing fine-tuning epochs (and possibly tuning other hyperparameters), can you get a testing accuracy higher than 0.86?
2. How to truncate a pair of sequences according to their ratio of length? Compare this pair truncation method and the one used in the SNLIBERTDataset class. What are their pros and cons?

16.6. Fine-Tuning BERT for Sequence-Level and Token-Level Applications — Dive into Deep Learning 1.0.3 documentation (d2l.ai)

In the previous sections of this chapter, we have designed different models for natural language processing applications, such as based on RNNs, CNNs, attention, and MLPs. These models are helpful when there is space or time constraint, however, crafting a specific model for every natural language processing task is practically infeasible. In Section 15.8, we introduced a pretraining model, BERT, that requires minimal architecture changes for a wide range of natural language processing tasks. On the one hand, at the time of its proposal, BERT improved the state of the art on various natural language processing tasks. On the other hand, as noted in Section 15.10, the two versions of the original BERT model come with 110 million and 340 million parameters. Thus, when there are sufficient computational resources, we may consider fine-tuning BERT for downstream natural language processing applications.

이 장의 이전 섹션에서는 RNN, CNN, Attention 및 MLP를 기반으로 하는 자연어 처리 애플리케이션을 위한 다양한 모델을 설계했습니다. 이러한 모델은 공간이나 시간 제약이 있을 때 유용하지만 모든 자연어 처리 작업에 대한 특정 모델을 만드는 것은 사실상 불가능합니다. 섹션 15.8에서는 광범위한 자연어 처리 작업에 대해 최소한의 아키텍처 변경이 필요한 사전 훈련 모델인 BERT를 소개했습니다. 한편, BERT는 제안 당시 다양한 자연어 처리 작업에 대한 최신 기술을 개선했습니다. 반면에 섹션 15.10에서 언급했듯이 원래 BERT 모델의 두 가지 버전에는 1억 1천만 개와 3억 4천만 개의 매개 변수가 있습니다. 따라서 계산 리소스가 충분할 경우 다운스트림 자연어 처리 애플리케이션을 위해 BERT를 미세 조정하는 것을 고려할 수 있습니다.

In the following, we generalize a subset of natural language processing applications as sequence-level and token-level. On the sequence level, we introduce how to transform the BERT representation of the text input to the output label in single text classification and text pair classification or regression. On the token level, we will briefly introduce new applications such as text tagging and question answering and shed light on how BERT can represent their inputs and get transformed into output labels. During fine-tuning, the “minimal architecture changes” required by BERT across different applications are the extra fully connected layers. During supervised learning of a downstream application, parameters of the extra layers are learned from scratch while all the parameters in the pretrained BERT model are fine-tuned.

다음에서는 자연어 처리 애플리케이션의 하위 집합을 시퀀스 수준 및 토큰 수준으로 일반화합니다. 시퀀스 수준에서는 단일 텍스트 분류 및 텍스트 쌍 분류 또는 회귀에서 텍스트 입력의 BERT 표현을 출력 레이블로 변환하는 방법을 소개합니다. 토큰 수준에서는 텍스트 태깅 및 질문 답변과 같은 새로운 애플리케이션을 간략하게 소개하고 BERT가 입력을 표현하고 출력 레이블로 변환하는 방법을 조명합니다. 미세 조정 중에 다양한 애플리케이션 전반에 걸쳐 BERT에 필요한 "최소 아키텍처 변경"은 추가로 완전히 연결된 레이어입니다. 다운스트림 애플리케이션의 지도 학습 중에 추가 레이어의 매개변수는 사전 학습된 BERT 모델의 모든 매개변수가 미세 조정되는 동안 처음부터 학습됩니다.

16.6.1. Single Text Classification

Single text classification takes a single text sequence as input and outputs its classification result. Besides sentiment analysis that we have studied in this chapter, the Corpus of Linguistic Acceptability (CoLA) is also a dataset for single text classification, judging whether a given sentence is grammatically acceptable or not (Warstadt et al., 2019). For instance, “I should study.” is acceptable but “I should studying.” is not.

단일 텍스트 분류는 단일 텍스트 시퀀스를 입력으로 사용하고 해당 분류 결과를 출력합니다. 이 장에서 연구한 감정 분석 외에도 CoLA(언어적 수용성 코퍼스)는 주어진 문장이 문법적으로 수용 가능한지 여부를 판단하는 단일 텍스트 분류를 위한 데이터 세트이기도 합니다(Warstadt et al., 2019). 예를 들어, “I should study.” 는 괜찮지만 “I should studying” 문법적으로 틀리다.

Section 15.8 describes the input representation of BERT. The BERT input sequence unambiguously represents both single text and text pairs, where the special classification token “<cls>” is used for sequence classification and the special classification token “<sep>” marks the end of single text or separates a pair of text. As shown in Fig. 16.6.1, in single text classification applications, the BERT representation of the special classification token “<cls>” encodes the information of the entire input text sequence. As the representation of the input single text, it will be fed into a small MLP consisting of fully connected (dense) layers to output the distribution of all the discrete label values.

섹션 15.8에서는 BERT의 입력 표현을 설명합니다. BERT 입력 시퀀스는 단일 텍스트와 텍스트 쌍을 모두 명확하게 나타냅니다. 여기서 특수 분류 토큰 "<cls>"는 시퀀스 분류에 사용되고 특수 분류 토큰 "<sep>"은 단일 텍스트의 끝을 표시하거나 텍스트 쌍을 구분합니다. . 그림 16.6.1에서 볼 수 있듯이 단일 텍스트 분류 응용 프로그램에서 특수 분류 토큰 "<cls>"의 BERT 표현은 전체 입력 텍스트 시퀀스의 정보를 인코딩합니다. 입력된 단일 텍스트의 표현으로서 완전히 연결된(조밀한) 레이어로 구성된 작은 MLP에 공급되어 모든 개별 레이블 값의 분포를 출력합니다.

16.6.2. Text Pair Classification or Regression

We have also examined natural language inference in this chapter. It belongs to text pair classification, a type of application classifying a pair of text.

우리는 또한 이 장에서 자연어 추론을 조사했습니다. 텍스트 쌍 분류(text pair classification)는 텍스트 쌍을 분류하는 애플리케이션 유형에 속합니다.

Taking a pair of text as input but outputting a continuous value, semantic textual similarity is a popular text pair regression task. This task measures semantic similarity of sentences. For instance, in the Semantic Textual Similarity Benchmark dataset, the similarity score of a pair of sentences is an ordinal scale ranging from 0 (no meaning overlap) to 5 (meaning equivalence) (Cer et al., 2017). The goal is to predict these scores. Examples from the Semantic Textual Similarity Benchmark dataset include (sentence 1, sentence 2, similarity score):

한 쌍의 텍스트를 입력으로 사용하지만 연속 값을 출력하는 의미론적 텍스트 유사성은 널리 사용되는 텍스트 쌍 회귀 작업입니다. 이 작업은 문장의 의미적 유사성을 측정합니다. 예를 들어 의미론적 텍스트 유사성 벤치마크 데이터세트에서 한 쌍의 문장의 유사성 점수는 0(의미 중첩 없음)에서 5(동등성을 의미) 범위의 순서 척도입니다(Cer et al., 2017). 목표는 이러한 점수를 예측하는 것입니다. 의미론적 텍스트 유사성 벤치마크 데이터 세트의 예는 다음과 같습니다(문장 1, 문장 2, 유사성 점수).

• “A plane is taking off.”, “An air plane is taking off.”, 5.000;
• “비행기가 이륙하고 있습니다.”, “비행기가 이륙하고 있습니다.”, 5.000;
• “A woman is eating something.”, “A woman is eating meat.”, 3.000;
• “여자가 뭔가를 먹고 있어요.”, “여자가 고기를 먹고 있어요.”, 3.000;
• “A woman is dancing.”, “A man is talking.”, 0.000.
• “여자가 춤을 추고 있다.”, “남자가 말하고 있다.”, 0.000.

Comparing with single text classification in Fig. 16.6.1, fine-tuning BERT for text pair classification in Fig. 16.6.2 is different in the input representation. For text pair regression tasks such as semantic textual similarity, trivial changes can be applied such as outputting a continuous label value and using the mean squared loss: they are common for regression.

그림 16.6.1의 단일 텍스트 분류와 비교하면 그림 16.6.2의 텍스트 쌍 분류를 위한 BERT 미세 조정은 입력 표현이 다릅니다. 의미론적 텍스트 유사성과 같은 텍스트 쌍 회귀 작업의 경우 연속 레이블 값을 출력하고 평균 제곱 손실을 사용하는 등 사소한 변경 사항을 적용할 수 있습니다. 이는 회귀에서 일반적입니다.

16.6.3. Text Tagging

Now let’s consider token-level tasks, such as text tagging, where each token is assigned a label. Among text tagging tasks, part-of-speech tagging assigns each word a part-of-speech tag (e.g., adjective and determiner) according to the role of the word in the sentence. For example, according to the Penn Treebank II tag set, the sentence “John Smith ’s car is new” should be tagged as “NNP (noun, proper singular) NNP POS (possessive ending) NN (noun, singular or mass) VB (verb, base form) JJ (adjective)”.

이제 각 토큰에 레이블이 할당되는 텍스트 태그 지정과 같은 토큰 수준 작업을 고려해 보겠습니다. 텍스트 태깅 작업 중에서 품사 태깅은 문장에서 단어의 역할에 따라 각 단어에 품사 태그(예: 형용사 및 한정사)를 할당합니다. 예를 들어 Penn Treebank II 태그 세트에 따르면 "John Smith's car is new"라는 문장은 "NNP(명사, 고유 단수) NNP POS(소유 어미) NN(명사, 단수 또는 대량) VB로 태그되어야 합니다. (동사, 기본형) JJ (형용사)”.

Fine-tuning BERT for text tagging applications is illustrated in Fig. 16.6.3. Comparing with Fig. 16.6.1, the only distinction lies in that in text tagging, the BERT representation of every token of the input text is fed into the same extra fully connected layers to output the label of the token, such as a part-of-speech tag.

텍스트 태깅 애플리케이션을 위한 BERT 미세 조정은 그림 16.6.3에 설명되어 있습니다. 그림 16.6.1과 비교하면 유일한 차이점은 텍스트 태깅에 있다는 것입니다. 입력 텍스트의 모든 토큰에 대한 BERT 표현은 품사 태그와 같은 토큰의 레이블을 출력하기 위해 동일한 추가 완전히 연결된 레이어에 공급됩니다.

16.6.4. Question Answering

As another token-level application, question answering reflects capabilities of reading comprehension. For example, the Stanford Question Answering Dataset (SQuAD v1.1) consists of reading passages and questions, where the answer to every question is just a segment of text (text span) from the passage that the question is about (Rajpurkar et al., 2016). To explain, consider a passage “Some experts report that a mask’s efficacy is inconclusive. However, mask makers insist that their products, such as N95 respirator masks, can guard against the virus.” and a question “Who say that N95 respirator masks can guard against the virus?”. The answer should be the text span “mask makers” in the passage. Thus, the goal in SQuAD v1.1 is to predict the start and end of the text span in the passage given a pair of question and passage.

또 다른 토큰 수준 응용 프로그램인 질문 답변은 독해 능력을 반영합니다. 예를 들어, Stanford 질문 응답 데이터 세트(SQuAD v1.1)는 읽기 구절과 질문으로 구성되며, 모든 질문에 대한 대답은 질문에 관한 구절의 텍스트 세그먼트(텍스트 범위)입니다(Rajpurkar et al. , 2016). 설명하려면 “일부 전문가들은 마스크의 효능이 확실하지 않다고 보고합니다. 그러나 마스크 제조업체들은 N95 마스크와 같은 자사 제품이 바이러스를 예방할 수 있다고 주장합니다.” 그리고 “N95 마스크가 바이러스를 예방할 수 있다고 누가 말합니까?”라는 질문. 대답은 해당 구절의 "마스크 제작자"라는 텍스트 범위여야 합니다. 따라서 SQuAD v1.1의 목표는 한 쌍의 질문과 지문이 주어진 지문에서 텍스트 범위의 시작과 끝을 예측하는 것입니다.

To fine-tune BERT for question answering, the question and passage are packed as the first and second text sequence, respectively, in the input of BERT. To predict the position of the start of the text span, the same additional fully connected layer will transform the BERT representation of any token from the passage of position i into a scalar score si. Such scores of all the passage tokens are further transformed by the softmax operation into a probability distribution, so that each token position i in the passage is assigned a probability pi of being the start of the text span. Predicting the end of the text span is the same as above, except that parameters in its additional fully connected layer are independent from those for predicting the start. When predicting the end, any passage token of position i is transformed by the same fully connected layer into a scalar score ei. Fig. 16.6.4 depicts fine-tuning BERT for question answering.

질문 답변을 위해 BERT를 미세 조정하기 위해 질문과 구절은 BERT 입력에서 각각 첫 번째 및 두 번째 텍스트 시퀀스로 패킹됩니다. 텍스트 범위의 시작 위치를 예측하기 위해 동일한 추가 완전 연결 레이어는 위치 i의 통과에서 모든 토큰의 BERT 표현을 스칼라 점수 si로 변환합니다. 모든 구절 토큰의 이러한 점수는 소프트맥스 연산에 의해 확률 분포로 추가로 변환되어 구절의 각 토큰 위치 i에 텍스트 범위의 시작이 될 확률 pi가 할당됩니다. 텍스트 범위의 끝을 예측하는 것은 추가 완전 연결 레이어의 매개 변수가 시작 예측을 위한 매개 변수와 독립적이라는 점을 제외하면 위와 동일합니다. 끝을 예측할 때 위치 i의 모든 통과 토큰은 동일한 완전 연결 레이어에 의해 스칼라 점수 ei로 변환됩니다. 그림 16.6.4는 질문 응답을 위한 BERT의 미세 조정을 보여줍니다.

For question answering, the supervised learning’s training objective is as straightforward as maximizing the log-likelihoods of the ground-truth start and end positions. When predicting the span, we can compute the score si+ej for a valid span from position i to position j (i≤j), and output the span with the highest score.

질문 답변의 경우 지도 학습의 훈련 목표는 실제 시작 및 끝 위치의 로그 가능성을 최대화하는 것만큼 간단합니다. 스팬을 예측할 때 i 위치에서 j 위치(i≤j)까지 유효한 스팬에 대해 점수 si+ej를 계산하고 점수가 가장 높은 스팬을 출력할 수 있습니다.

16.6.5. Summary

• BERT requires minimal architecture changes (extra fully connected layers) for sequence-level and token-level natural language processing applications, such as single text classification (e.g., sentiment analysis and testing linguistic acceptability), text pair classification or regression (e.g., natural language inference and semantic textual similarity), text tagging (e.g., part-of-speech tagging), and question answering.
  
  BERT는 single text classification, text pair classification or regression, text tagging, question answering 같은 sequence-level과 token level natural language processing applications에 대해 최소한의 아키텍쳐 변경만으로 task 를 수행할 수 있도록 함.
  
  
• During supervised learning of a downstream application, parameters of the extra layers are learned from scratch while all the parameters in the pretrained BERT model are fine-tuned.
  
  다운스트림 애플리케이션의 지도 학습 중에 추가 레이어의 매개변수는 사전 학습된 BERT 모델의 모든 매개변수가 미세 조정되는 동안 처음부터 학습됩니다.

16.6.6. Exercises

1. Let’s design a search engine algorithm for news articles. When the system receives an query (e.g., “oil industry during the coronavirus outbreak”), it should return a ranked list of news articles that are most relevant to the query. Suppose that we have a huge pool of news articles and a large number of queries. To simplify the problem, suppose that the most relevant article has been labeled for each query. How can we apply negative sampling (see Section 15.2.1) and BERT in the algorithm design?
2. How can we leverage BERT in training language models?
3. Can we leverage BERT in machine translation?

16.4. Natural Language Inference and the Dataset — Dive into Deep Learning 1.0.3 documentation (d2l.ai)

16.5. Natural Language Inference: Using Attention

We introduced the natural language inference task and the SNLI dataset in Section 16.4. In view of many models that are based on complex and deep architectures, Parikh et al. (2016) proposed to address natural language inference with attention mechanisms and called it a “decomposable attention model”. This results in a model without recurrent or convolutional layers, achieving the best result at the time on the SNLI dataset with much fewer parameters. In this section, we will describe and implement this attention-based method (with MLPs) for natural language inference, as depicted in Fig. 16.5.1.

섹션 16.4에서 자연어 추론 작업과 SNLI 데이터 세트를 소개했습니다. 복잡하고 심층적인 아키텍처를 기반으로 하는 많은 모델을 고려하여 Parikh et al. (2016)은 Attention 메커니즘을 통해 자연어 추론을 처리할 것을 제안하고 이를 "분해 가능한 Attention 모델"이라고 불렀습니다. 그 결과 순환 또는 컨벌루션 레이어가 없는 모델이 생성되어 훨씬 적은 매개변수를 사용하여 SNLI 데이터세트에서 당시 최상의 결과를 얻을 수 있습니다. 이 섹션에서는 그림 16.5.1에 설명된 대로 자연어 추론을 위한 Attention  기반 방법(MLP 사용)을 설명하고 구현합니다.

16.5.1. The Model

Simpler than preserving the order of tokens in premises and hypotheses, we can just align tokens in one text sequence to every token in the other, and vice versa, then compare and aggregate such information to predict the logical relationships between premises and hypotheses. Similar to alignment of tokens between source and target sentences in machine translation, the alignment of tokens between premises and hypotheses can be neatly accomplished by attention mechanisms.

전제와 가설에서 토큰의 순서를 유지하는 것보다 더 간단한 것은 한 텍스트 시퀀스의 토큰을 다른 텍스트 시퀀스의 모든 토큰에 정렬하고 그 반대의 경우도 마찬가지입니다. 그런 다음 이러한 정보를 비교하고 집계하여 전제와 가설 사이의 논리적 관계를 예측할 수 있습니다. 기계 번역에서 소스 문장과 대상 문장 사이의 토큰 정렬과 유사하게 전제와 가설 사이의 토큰 정렬은 어텐션 메커니즘을 통해 깔끔하게 수행될 수 있습니다.

Fig. 16.5.2 depicts the natural language inference method using attention mechanisms. At a high level, it consists of three jointly trained steps: attending, comparing, and aggregating. We will illustrate them step by step in the following.

그림 16.5.2는 Attention 메커니즘을 이용한 자연어 추론 방법을 보여줍니다. high level concept을 보면 참석 attending, 비교 comparing, 집계 aggregating라는 세 가지 공동 훈련 단계로 구성됩니다. 다음에서는 이를 단계별로 설명하겠습니다.

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

16.5.1.1. Attending

The first step is to align tokens in one text sequence to each token in the other sequence. Suppose that the premise is “i do need sleep” and the hypothesis is “i am tired”. Due to semantical similarity, we may wish to align “i” in the hypothesis with “i” in the premise, and align “tired” in the hypothesis with “sleep” in the premise. Likewise, we may wish to align “i” in the premise with “i” in the hypothesis, and align “need” and “sleep” in the premise with “tired” in the hypothesis. Note that such alignment is soft using weighted average, where ideally large weights are associated with the tokens to be aligned. For ease of demonstration, Fig. 16.5.2 shows such alignment in a hard way.

첫 번째 단계는 한 텍스트 시퀀스의 토큰을 다른 시퀀스의 각 토큰에 정렬하는 것입니다. 전제가 "i do need sleep"이고 가설은 "i am tired"라고 가정해보자. 의미적 유사성으로 인해 가설의 "i"를 전제의 "i"와 정렬하고 가설의 "tired"를 전제의 "sleep"과 정렬할 수 있습니다. 마찬가지로, 전제의 "i"를 가설의 "i"와 정렬하고 전제의 "need"와 "sleep"을 가설의 "tired"와 정렬할 수 있습니다. 이러한 정렬은 가중 평균을 사용하여 유연하게 이루어지며, 이상적으로는 큰 가중치가 정렬할 토큰과 연관되어 있습니다. 설명을 쉽게 하기 위해 그림 16.5.2에서는 이러한 정렬을 어려운 방식으로 보여줍니다.

Now we describe the soft alignment using attention mechanisms in more detail. Denote by A=(a1,...,am) and B=(b1,...,bn) the premise and hypothesis, whose number of tokens are m and n, respectively, where ai,bj∈ℝ**d (i=1,...,m,j=1,...,n) is a d-dimensional word vector. For soft alignment, we compute the attention weights eij∈ℝ as 

이제 attention  메커니즘을 사용하여 소프트 정렬을 더 자세히 설명합니다. 전제와 가설을 A=(a1,...,am) 및 B=(b1,...,bn)으로 표시합니다. 여기서 토큰 수는 각각 m과 n입니다. 여기서 ai,bj∈ℝ**d (i=1,...,m,j=1,...,n)은 d차원 단어 벡터입니다. 소프트 정렬을 위해 관심 가중치 attention weights eij∈ℝ를 다음과 같이 계산합니다.

where the function f is an MLP defined in the following mlp function. The output dimension of f is specified by the num_hiddens argument of mlp.

여기서 함수 f는 다음 mlp 함수에 정의된 MLP입니다. f의 출력 차원은 mlp의 num_hiddens 인수로 지정됩니다.

def mlp(num_inputs, num_hiddens, flatten):
    net = []
    net.append(nn.Dropout(0.2))
    net.append(nn.Linear(num_inputs, num_hiddens))
    net.append(nn.ReLU())
    if flatten:
        net.append(nn.Flatten(start_dim=1))
    net.append(nn.Dropout(0.2))
    net.append(nn.Linear(num_hiddens, num_hiddens))
    net.append(nn.ReLU())
    if flatten:
        net.append(nn.Flatten(start_dim=1))
    return nn.Sequential(*net)

이 코드는 다층 퍼셉트론(MLP) 네트워크를 정의하는 함수인 mlp를 생성하는 파이토치 코드입니다. 이 함수는 네트워크의 구조를 정의하고 반환합니다. 코드의 작동 방식을 설명하겠습니다.

1. 함수 정의:
   • def mlp(num_inputs, num_hiddens, flatten):: MLP 네트워크를 정의하는 함수입니다. 인자로 입력 특성의 수(num_inputs), 은닉층의 유닛 수(num_hiddens), 평탄화 여부(flatten)를 받습니다.
2. 네트워크 구성:
   • net = []: 빈 리스트를 생성하여 네트워크 레이어를 순서대로 추가할 예정입니다.
   • net.append(nn.Dropout(0.2)): 드롭아웃 레이어를 추가합니다. 드롭아웃은 과적합을 방지하기 위해 사용됩니다.
   • net.append(nn.Linear(num_inputs, num_hiddens)): 완전 연결 레이어를 추가합니다. 입력 특성 수에서 은닉층 유닛 수로 연결됩니다.
   • net.append(nn.ReLU()): ReLU 활성화 함수를 추가합니다. 이 함수는 비선형성을 네트워크에 추가합니다.
   • if flatten: ...: 만약 flatten이 True라면, 평탄화 레이어(nn.Flatten)를 추가합니다. 평탄화는 2D 입력을 1D로 변환합니다.
   • 위의 네 레이어를 한 번 더 추가합니다. 이것은 두 번째 은닉층과 ReLU 활성화 함수를 의미합니다.
3. 네트워크 반환:
   • return nn.Sequential(*net): 정의한 레이어들을 nn.Sequential 컨테이너로 묶어서 반환합니다. 이것은 순차적으로 레이어가 실행되는 MLP 네트워크를 나타냅니다.

결과적으로, 이 함수는 주어진 입력 특성 수와 은닉층 유닛 수에 따라 다층 퍼셉트론(MLP) 네트워크를 생성하고, 평탄화 여부에 따라 네트워크 구조를 조절하여 반환합니다.

It should be highlighted that, in (16.5.1) f takes inputs ai and bj separately rather than takes a pair of them together as input. This decomposition trick leads to only m+n applications (linear complexity) of f rather than mn applications (quadratic complexity).

(16.5.1)에서 f는 ai와 bj를 입력으로 함께 사용하는 대신 입력 ai와 bj를 별도로 사용한다는 점을 강조해야 합니다. 이 분해 트릭은 mn 적용(2차 복잡도)이 아닌 f의 m+n 적용(선형 복잡도)만을 초래합니다.

Normalizing the attention weights in (16.5.1), we compute the weighted average of all the token vectors in the hypothesis to obtain representation of the hypothesis that is softly aligned with the token indexed by i in the premise:

(16.5.1)에서 어텐션 가중치를 정규화하여 가설의 모든 토큰 벡터의 가중 평균을 계산하여 전제에서 i로 인덱스된 토큰과 부드럽게 정렬되는 가설의 표현을 얻습니다.

Likewise, we compute soft alignment of premise tokens for each token indexed by j in the hypothesis:

마찬가지로 가설에서 j로 색인된 각 토큰에 대한 전제 토큰의 소프트 정렬을 계산합니다.

Below we define the Attend class to compute the soft alignment of hypotheses (beta) with input premises A and soft alignment of premises (alpha) with input hypotheses B.

아래에서는 입력 전제 A와 가설(베타)의 소프트 정렬 및 입력 가설 B와 전제(알파)의 소프트 정렬을 계산하기 위해 Attend 클래스를 정의합니다.

class Attend(nn.Module):
    def __init__(self, num_inputs, num_hiddens, **kwargs):
        super(Attend, self).__init__(**kwargs)
        self.f = mlp(num_inputs, num_hiddens, flatten=False)

    def forward(self, A, B):
        # Shape of `A`/`B`: (`batch_size`, no. of tokens in sequence A/B,
        # `embed_size`)
        # Shape of `f_A`/`f_B`: (`batch_size`, no. of tokens in sequence A/B,
        # `num_hiddens`)
        f_A = self.f(A)
        f_B = self.f(B)
        # Shape of `e`: (`batch_size`, no. of tokens in sequence A,
        # no. of tokens in sequence B)
        e = torch.bmm(f_A, f_B.permute(0, 2, 1))
        # Shape of `beta`: (`batch_size`, no. of tokens in sequence A,
        # `embed_size`), where sequence B is softly aligned with each token
        # (axis 1 of `beta`) in sequence A
        beta = torch.bmm(F.softmax(e, dim=-1), B)
        # Shape of `alpha`: (`batch_size`, no. of tokens in sequence B,
        # `embed_size`), where sequence A is softly aligned with each token
        # (axis 1 of `alpha`) in sequence B
        alpha = torch.bmm(F.softmax(e.permute(0, 2, 1), dim=-1), A)
        return beta, alpha

이 코드는 "Attend"라는 클래스를 정의하는 파이토치 코드로, 시퀀스 A와 시퀀스 B 간의 어텐션 메커니즘을 구현합니다. 코드의 작동 방식을 설명하겠습니다.

1. 클래스 정의:
   • class Attend(nn.Module):: Attend 클래스를 정의합니다. 이 클래스는 파이토치의 nn.Module을 상속합니다.
2. 생성자(__init__) 메서드:
   • def __init__(self, num_inputs, num_hiddens, **kwargs):: Attend 클래스의 생성자 메서드입니다. 인자로 num_inputs (입력 특성의 수), num_hiddens (은닉층의 유닛 수)를 받습니다.
   • self.f = mlp(num_inputs, num_hiddens, flatten=False): Attend 클래스 내에서 사용할 MLP 네트워크 f를 생성합니다. mlp 함수를 호출하여 생성한 MLP 네트워크를 self.f로 저장합니다.
3. forward 메서드:
   • def forward(self, A, B):: Attend 클래스의 forward 메서드입니다. 인자로 시퀀스 A와 시퀀스 B를 받습니다.
   • f_A = self.f(A), f_B = self.f(B): 시퀀스 A와 시퀀스 B에 각각 MLP 네트워크를 적용하여 특성을 추출합니다.
   • e = torch.bmm(f_A, f_B.permute(0, 2, 1)): 두 시퀀스 간의 유사도 점수를 계산합니다. f_A와 f_B의 내적을 계산하여 어텐션 스코어 행렬 e를 얻습니다.
   • beta = torch.bmm(F.softmax(e, dim=-1), B): 시퀀스 A에 대한 부드러운 어텐션 가중치를 계산하고, 이를 기반으로 시퀀스 B를 정렬합니다.
   • alpha = torch.bmm(F.softmax(e.permute(0, 2, 1), dim=-1), A): 시퀀스 B에 대한 부드러운 어텐션 가중치를 계산하고, 이를 기반으로 시퀀스 A를 정렬합니다.
   • return beta, alpha: 계산된 어텐션 가중치인 beta와 alpha를 반환합니다.

결과적으로, 이 코드는 시퀀스 A와 시퀀스 B 간의 어텐션을 계산하는 Attend 클래스를 정의하고, forward 메서드를 통해 어텐션 가중치를 계산하여 반환합니다. 이것은 주로 자연어 처리 태스크에서 활용되는 어텐션 메커니즘의 일부분입니다.

https://pytorch.org/docs/stable/generated/torch.bmm.html

https://blog.naver.com/gksthf4140/222986529109

https://pytorch.org/docs/stable/generated/torch.permute.html

http://iambeginnerdeveloper.tistory.com/215

https://pytorch.org/docs/stable/generated/torch.nn.Softmax.html

16.5.1.2. Comparing

In the next step, we compare a token in one sequence with the other sequence that is softly aligned with that token. Note that in soft alignment, all the tokens from one sequence, though with probably different attention weights, will be compared with a token in the other sequence. For easy of demonstration, Fig. 16.5.2 pairs tokens with aligned tokens in a hard way. For example, suppose that the attending step determines that “need” and “sleep” in the premise are both aligned with “tired” in the hypothesis, the pair “tired–need sleep” will be compared.

다음 단계에서는 한 시퀀스의 토큰을 해당 토큰과 소프트하게 정렬된 다른 시퀀스와 비교합니다. 소프트 정렬에서는 주의 가중치가 다를지라도 한 시퀀스의 모든 토큰이 다른 시퀀스의 토큰과 비교됩니다. 시연을 쉽게 하기 위해 그림 16.5.2에서는 토큰과 정렬된 토큰을 hard way으로 쌍으로 연결합니다. 예를 들어, 참석 attending  단계에서 전제 premise 의 "need"와 "sleep"이 모두 가설 hypothesis의 "tired"과 일치한다고 판단한다고 가정하면 "tired–need sleep" 쌍이 비교됩니다.

In the comparing step, we feed the concatenation (operator [⋅,⋅]) of tokens from one sequence and aligned tokens from the other sequence into a function g (an MLP):

비교 단계에서는 한 시퀀스의 토큰과 다른 시퀀스의 정렬된 토큰을 함수 g(MLP)에 연결(연산자 [⋅,⋅])합니다.

Soft Alignment란?

'Soft alignment'은 주어진 두 시퀀스 간의 상관 관계를 나타내는 방법 중 하나입니다. 이것은 자연어 처리와 기계 학습에서 자주 사용되며, 주로 시퀀스-시퀀스 모델, 언어 모델, 번역 모델 등에서 사용됩니다.

'Soft alignment'은 두 시퀀스 사이의 상호작용을 '단단한' 매칭이 아니라 각 요소 사이의 '소프트한' 매칭으로 표현합니다. 이것은 각 요소가 다른 요소와 얼마나 관련이 있는지를 확률적으로 표현합니다. 주로 다음과 같은 상황에서 사용됩니다.

1. 번역 모델 (Machine Translation): 소스 언어와 타겟 언어 간의 문장을 번역할 때, 각 소스 단어가 타겟 문장에서 어떻게 매핑되는지를 나타냅니다. Soft alignment은 각 소스 단어가 다른 언어의 단어와 얼마나 연관되어 있는지를 확률적으로 표현하여 번역 모델을 개선하는 데 사용됩니다.
   
   
2. 질의응답 (Question Answering): 주어진 질문과 문서에서 답변을 찾을 때, 문서의 각 단어가 질문과 어떻게 관련되어 있는지를 나타냅니다. 이것은 문서 내에서 답변을 찾는 데 도움이 됩니다.
   
   
3. 기계 독해 (Machine Reading Comprehension): 주어진 텍스트에서 특정 질문에 대한 답변을 찾는 작업에서 사용됩니다. 각 문장 또는 문단의 각 단어가 질문과 어떻게 관련되어 있는지를 표현합니다.
   
   

Soft alignment을 사용하면 정보를 효과적으로 전달하고 시퀀스 간의 관계를 모델링할 수 있습니다. 이것은 주어진 작업에 따라 적절한 가중치를 각 요소에 할당하는 데 도움이 됩니다. Soft alignment은 주로 확률 분포 또는 어텐션 메커니즘과 같은 방법을 사용하여 구현됩니다. 이러한 메커니즘은 각 요소 간의 상호작용을 확률적으로 모델링하는 방법을 제공하며, 이를 통해 다양한 자연어 처리 작업을 효과적으로 수행할 수 있게 됩니다.

In (16.5.4), vA,i is the comparison between token i in the premise and all the hypothesis tokens that are softly aligned with token i; while vB,j is the comparison between token j in the hypothesis and all the premise tokens that are softly aligned with token j. The following Compare class defines such as comparing step.

(16.5.4)에서 vA,i는 전제의 토큰 i와 토큰 i와 부드럽게 정렬된 모든 가설 토큰 간의 비교입니다. vB,j는 가설의 토큰 j와 토큰 j와 부드럽게 정렬된 모든 전제 토큰 간의 비교입니다. 다음 Compare 클래스는 비교 단계 등을 정의합니다.

class Compare(nn.Module):
    def __init__(self, num_inputs, num_hiddens, **kwargs):
        super(Compare, self).__init__(**kwargs)
        self.g = mlp(num_inputs, num_hiddens, flatten=False)

    def forward(self, A, B, beta, alpha):
        V_A = self.g(torch.cat([A, beta], dim=2))
        V_B = self.g(torch.cat([B, alpha], dim=2))
        return V_A, V_B

이 코드는 "Compare"라는 클래스를 정의하는 파이토치 코드로, 두 시퀀스 A와 B 간의 비교를 수행하는 부분입니다. 코드의 작동 방식을 설명하겠습니다.

1. 클래스 정의:
   • class Compare(nn.Module):: Compare 클래스를 정의합니다. 이 클래스는 파이토치의 nn.Module을 상속합니다.
2. 생성자(__init__) 메서드:
   • def __init__(self, num_inputs, num_hiddens, **kwargs):: Compare 클래스의 생성자 메서드입니다. 인자로 num_inputs (입력 특성의 수), num_hiddens (은닉층의 유닛 수)를 받습니다.
   • self.g = mlp(num_inputs, num_hiddens, flatten=False): Compare 클래스 내에서 사용할 MLP 네트워크 g를 생성합니다. mlp 함수를 호출하여 생성한 MLP 네트워크를 self.g로 저장합니다.
3. forward 메서드:
   • def forward(self, A, B, beta, alpha):: Compare 클래스의 forward 메서드입니다. 인자로 시퀀스 A, 시퀀스 B, 그리고 Attend 클래스에서 얻은 어텐션 가중치 beta와 alpha를 받습니다.
   • V_A = self.g(torch.cat([A, beta], dim=2)): 시퀀스 A와 해당 시퀀스에 부드러운 어텐션을 적용한 beta를 합치고, MLP 네트워크 g를 사용하여 시퀀스 A에 대한 특성 벡터 V_A를 계산합니다.
   • V_B = self.g(torch.cat([B, alpha], dim=2)): 시퀀스 B와 해당 시퀀스에 부드러운 어텐션을 적용한 alpha를 합치고, MLP 네트워크 g를 사용하여 시퀀스 B에 대한 특성 벡터 V_B를 계산합니다.
   • return V_A, V_B: 계산된 시퀀스 A와 B의 특성 벡터 V_A와 V_B를 반환합니다.

결과적으로, 이 코드는 두 시퀀스 A와 B 간의 비교를 수행하는 Compare 클래스를 정의하고, forward 메서드를 통해 각 시퀀스에 대한 특성 벡터 V_A와 V_B를 계산하여 반환합니다. 이것은 주로 자연어 처리 태스크에서 활용되는 비교 메커니즘의 일부분입니다.

16.5.1.3. Aggregating

With two sets of comparison vectors vA,i (i=1,…,m) and vB,j (j=1,…,n) on hand, in the last step we will aggregate such information to infer the logical relationship. We begin by summing up both sets:

두 세트의 비교 벡터 vA,i(i=1,…,m) 및 vB,j(j=1,…,n)를 사용하여 마지막 단계에서 이러한 정보를 집계하여 논리적 관계를 추론합니다. 두 세트를 요약하는 것으로 시작합니다.

Next we feed the concatenation of both summarization results into function ℎ (an MLP) to obtain the classification result of the logical relationship:

다음으로 두 요약 결과를 함수 ℎ(MLP)에 연결하여 논리적 관계의 분류 결과를 얻습니다.

The aggregation step is defined in the following Aggregate class.

집계 단계는 다음 Aggregate 클래스에 정의되어 있습니다.

class Aggregate(nn.Module):
    def __init__(self, num_inputs, num_hiddens, num_outputs, **kwargs):
        super(Aggregate, self).__init__(**kwargs)
        self.h = mlp(num_inputs, num_hiddens, flatten=True)
        self.linear = nn.Linear(num_hiddens, num_outputs)

    def forward(self, V_A, V_B):
        # Sum up both sets of comparison vectors
        V_A = V_A.sum(dim=1)
        V_B = V_B.sum(dim=1)
        # Feed the concatenation of both summarization results into an MLP
        Y_hat = self.linear(self.h(torch.cat([V_A, V_B], dim=1)))
        return Y_hat

이 코드는 "Aggregate"라는 클래스를 정의하는 파이토치 코드로, 두 집합 A와 B 간의 요약 및 집계 작업을 수행합니다. 코드의 작동 방식을 설명하겠습니다.

1. 클래스 정의:
   • class Aggregate(nn.Module):: Aggregate 클래스를 정의합니다. 이 클래스는 파이토치의 nn.Module을 상속합니다.
2. 생성자(__init__) 메서드:
   • def __init__(self, num_inputs, num_hiddens, num_outputs, **kwargs):: Aggregate 클래스의 생성자 메서드입니다. 인자로 num_inputs (입력 특성의 수), num_hiddens (은닉층의 유닛 수), num_outputs (출력 특성의 수)를 받습니다.
   • self.h = mlp(num_inputs, num_hiddens, flatten=True): 입력 특성에 대한 MLP 네트워크 h를 생성합니다. mlp 함수를 호출하여 생성한 MLP 네트워크를 self.h로 저장합니다.
   • self.linear = nn.Linear(num_hiddens, num_outputs): 선형 변환 레이어를 생성합니다. 이 레이어는 MLP 네트워크 h의 출력을 최종 출력 특성 수에 매핑합니다.
3. forward 메서드:
   • def forward(self, V_A, V_B):: Aggregate 클래스의 forward 메서드입니다. 인자로 두 집합 A와 B에 대한 특성 벡터 V_A와 V_B를 받습니다.
   • V_A = V_A.sum(dim=1), V_B = V_B.sum(dim=1): 두 집합의 비교 벡터를 각각 합산합니다. 각 집합 내의 벡터를 모두 합하여 집합을 하나의 벡터로 요약합니다.
   • Y_hat = self.linear(self.h(torch.cat([V_A, V_B], dim=1))): 합산된 두 집합의 요약 벡터를 연결하고, 이를 MLP 네트워크 h를 통과시켜 최종 출력 특성 벡터 Y_hat을 계산합니다.
   • return Y_hat: 계산된 출력 특성 벡터 Y_hat을 반환합니다.

결과적으로, 이 코드는 두 집합 A와 B 간의 요약과 집계를 수행하는 Aggregate 클래스를 정의하고, forward 메서드를 통해 두 집합의 특성 벡터를 합산하고 최종 예측을 계산합니다. 이것은 자연어 처리 및 비교 분류 작업에 사용될 수 있습니다.

16.5.1.4. Putting It All Together

By putting the attending, comparing, and aggregating steps together, we define the decomposable attention model to jointly train these three steps.

주의 attending, 비교 comparing 및 집계 aggregating  단계를 함께 배치하여 이 세 단계를 공동으로 훈련하는 분해 가능한 주의 모델을 정의합니다.

class DecomposableAttention(nn.Module):
    def __init__(self, vocab, embed_size, num_hiddens, num_inputs_attend=100,
                 num_inputs_compare=200, num_inputs_agg=400, **kwargs):
        super(DecomposableAttention, self).__init__(**kwargs)
        self.embedding = nn.Embedding(len(vocab), embed_size)
        self.attend = Attend(num_inputs_attend, num_hiddens)
        self.compare = Compare(num_inputs_compare, num_hiddens)
        # There are 3 possible outputs: entailment, contradiction, and neutral
        self.aggregate = Aggregate(num_inputs_agg, num_hiddens, num_outputs=3)

    def forward(self, X):
        premises, hypotheses = X
        A = self.embedding(premises)
        B = self.embedding(hypotheses)
        beta, alpha = self.attend(A, B)
        V_A, V_B = self.compare(A, B, beta, alpha)
        Y_hat = self.aggregate(V_A, V_B)
        return Y_hat

이 코드는 "DecomposableAttention"이라는 클래스를 정의하는 파이토치 코드로, 자연어 처리 작업에서 사용되는 디코마블 어텐션 모델을 구현합니다. 코드의 작동 방식을 설명하겠습니다.

1. 클래스 정의:
   • class DecomposableAttention(nn.Module):: DecomposableAttention 클래스를 정의합니다. 이 클래스는 파이토치의 nn.Module을 상속합니다.
2. 생성자(__init__) 메서드:
   • def __init__(self, vocab, embed_size, num_hiddens, num_inputs_attend=100, num_inputs_compare=200, num_inputs_agg=400, **kwargs):: DecomposableAttention 클래스의 생성자 메서드입니다. 인자로 다양한 하이퍼파라미터를 받습니다.
   • self.embedding = nn.Embedding(len(vocab), embed_size): 입력 토큰을 임베딩하는 데 사용되는 임베딩 레이어를 생성합니다.
   • self.attend = Attend(num_inputs_attend, num_hiddens): Attend 클래스를 사용하여 어텐션 메커니즘을 구현합니다.
   • self.compare = Compare(num_inputs_compare, num_hiddens): Compare 클래스를 사용하여 두 시퀀스의 비교를 수행합니다.
   • self.aggregate = Aggregate(num_inputs_agg, num_hiddens, num_outputs=3): Aggregate 클래스를 사용하여 최종 결과를 집계합니다. 가능한 출력은 entailment(인과 관계), contradiction(모순), neutral(중립) 세 가지입니다.
3. forward 메서드:
   • def forward(self, X):: DecomposableAttention 클래스의 forward 메서드입니다. 인자로 토큰화된 전처리된 시퀀스 쌍 X를 받습니다.
   • premises, hypotheses = X: 입력으로 받은 시퀀스 쌍 X를 premise(전제)와 hypothesis(가설)로 나눕니다.
   • A = self.embedding(premises), B = self.embedding(hypotheses): 각각의 premise와 hypothesis를 임베딩하여 시퀀스 A와 B를 얻습니다.
   • beta, alpha = self.attend(A, B): Attend 클래스를 사용하여 어텐션 가중치 beta와 alpha를 계산합니다.
   • V_A, V_B = self.compare(A, B, beta, alpha): Compare 클래스를 사용하여 시퀀스 A와 B 간의 비교를 수행하고, 결과인 V_A와 V_B를 얻습니다.
   • Y_hat = self.aggregate(V_A, V_B): Aggregate 클래스를 사용하여 최종 결과를 집계하고, 예측 결과인 Y_hat을 반환합니다.

이 코드는 자연어 처리 작업에서 시퀀스 쌍에 대한 디코마블 어텐션 모델을 구현합니다. 이 모델은 시퀀스 A와 B 간의 관계를 예측하는 데 사용될 수 있습니다.

16.5.2. Training and Evaluating the Model

Now we will train and evaluate the defined decomposable attention model on the SNLI dataset. We begin by reading the dataset.

이제 SNLI 데이터 세트에서 정의된 분해 가능한 주의 모델을 훈련하고 평가하겠습니다. 데이터세트를 읽는 것부터 시작합니다.

16.5.2.1. Reading the dataset

We download and read the SNLI dataset using the function defined in Section 16.4. The batch size and sequence length are set to 256 and 50, respectively.

섹션 16.4에 정의된 함수를 사용하여 SNLI 데이터 세트를 다운로드하고 읽습니다. 배치 크기와 시퀀스 길이는 각각 256과 50으로 설정됩니다.

batch_size, num_steps = 256, 50
train_iter, test_iter, vocab = d2l.load_data_snli(batch_size, num_steps)

이 코드는 SNLI 데이터셋을 로드하고 데이터를 미니배치로 나누는 작업을 수행합니다.

• batch_size: 미니배치의 크기를 설정합니다. 각 미니배치에 포함될 데이터 포인트의 수입니다. 이 경우 256으로 설정됩니다.
• num_steps: 시퀀스의 길이를 설정합니다. 각 입력 시퀀스는 이 길이로 자르거나 패딩됩니다. 이 경우 50으로 설정됩니다.
• train_iter: 훈련 데이터셋을 나타내는 데이터 로더(iterator)입니다. 이 데이터 로더는 미니배치 단위로 훈련 데이터를 제공합니다.
• test_iter: 테스트 데이터셋을 나타내는 데이터 로더(iterator)입니다. 이 데이터 로더는 미니배치 단위로 테스트 데이터를 제공합니다.
• vocab: 데이터셋에서 생성된 어휘(vocabulary)입니다. 어휘는 텍스트 데이터를 숫자로 변환하는 데 사용됩니다.

즉, 이 코드는 SNLI 데이터셋을 설정한 미니배치 크기와 시퀀스 길이에 따라 로드하고 데이터를 훈련용과 테스트용으로 분할합니다. 이렇게 분할된 데이터를 모델 학습 및 평가에 사용할 수 있게 합니다.

Downloading ../data/snli_1.0.zip from https://nlp.stanford.edu/projects/snli/snli_1.0.zip...
read 549367 examples
read 9824 examples

16.5.2.2. Creating the Model

We use the pretrained 100-dimensional GloVe embedding to represent the input tokens. Thus, we predefine the dimension of vectors ai and bj in (16.5.1) as 100. The output dimension of functions f in (16.5.1) and g in (16.5.4) is set to 200. Then we create a model instance, initialize its parameters, and load the GloVe embedding to initialize vectors of input tokens.

우리는 사전 훈련된 100차원 GloVe 임베딩을 사용하여 입력 토큰을 나타냅니다. 따라서 (16.5.1)의 벡터 ai 및 bj의 차원을 100으로 미리 정의합니다. 함수 f in (16.5.1) 및 g in (16.5.4)의 출력 차원은 200으로 설정됩니다. 그런 다음 모델을 생성합니다. 예를 들어 매개변수를 초기화하고 GloVe 임베딩을 로드하여 입력 토큰의 벡터를 초기화합니다.

embed_size, num_hiddens, devices = 100, 200, d2l.try_all_gpus()
net = DecomposableAttention(vocab, embed_size, num_hiddens)
glove_embedding = d2l.TokenEmbedding('glove.6b.100d')
embeds = glove_embedding[vocab.idx_to_token]
net.embedding.weight.data.copy_(embeds);

이 코드는 SNLI 분류 모델을 위한 Decomposable Attention 모델을 설정하고, 사전 훈련된 GloVe 임베딩을 사용하여 모델의 임베딩 레이어 초기화를 수행합니다.

• embed_size: 임베딩 차원의 크기를 설정합니다. 각 단어의 임베딩 벡터는 이 차원의 크기를 갖습니다. 이 경우 100으로 설정됩니다.
• num_hiddens: 은닉 레이어의 크기를 설정합니다. 모델의 은닉 상태나 특성 벡터의 크기를 나타냅니다. 이 경우 200으로 설정됩니다.
• devices: 사용 가능한 GPU 디바이스(device) 목록을 확인합니다. 여기서 d2l.try_all_gpus()를 사용하여 가능한 모든 GPU를 선택합니다. 이렇게 선택한 GPU에서 모델이 학습됩니다.
• net: DecomposableAttention 클래스의 인스턴스를 생성합니다. 이 모델은 토큰 임베딩, 어텐션, 비교, 집계 레이어로 구성됩니다.
• glove_embedding: GloVe 임베딩을 로드합니다. GloVe는 사전 훈련된 단어 임베딩 모델로, 단어를 벡터로 표현합니다. 'glove.6b.100d'는 6억 단어의 텍스트 데이터를 사용하여 학습한 100차원의 GloVe 임베딩 모델을 지칭합니다.
• embeds: GloVe 임베딩 모델에서 현재 데이터셋 어휘(vocabulary)에 있는 단어들에 해당하는 임베딩 벡터를 가져옵니다.
• net.embedding.weight.data.copy_(embeds): 모델의 임베딩 레이어의 가중치를 GloVe 임베딩 벡터로 초기화합니다. 이를 통해 모델은 사전 훈련된 단어 임베딩을 활용하여 학습을 시작할 수 있습니다.

이 코드는 모델의 초기화 단계로, 토큰 임베딩을 사전 훈련된 GloVe 임베딩으로 초기화하여 모델이 텍스트 데이터를 이해하고 활용할 수 있도록 준비합니다.

Downloading ../data/glove.6B.100d.zip from http://d2l-data.s3-accelerate.amazonaws.com/glove.6B.100d.zip...

16.5.2.3. Training and Evaluating the Model

In contrast to the split_batch function in Section 13.5 that takes single inputs such as text sequences (or images), we define a split_batch_multi_inputs function to take multiple inputs such as premises and hypotheses in minibatches.

텍스트 시퀀스(또는 이미지)와 같은 단일 입력을 취하는 섹션 13.5의 Split_batch 함수와 달리 우리는 minibatch의 전제 및 가설과 같은 여러 입력을 취하는 Split_batch_multi_inputs 함수를 정의합니다.

#@save
def split_batch_multi_inputs(X, y, devices):
    """Split multi-input `X` and `y` into multiple devices."""
    X = list(zip(*[gluon.utils.split_and_load(
        feature, devices, even_split=False) for feature in X]))
    return (X, gluon.utils.split_and_load(y, devices, even_split=False))

이 코드는 주어진 X와 y를 여러 디바이스로 분할하는 함수를 정의합니다. 이 함수는 주로 딥러닝 모델을 여러 GPU 또는 디바이스에 병렬로 실행할 때 사용됩니다. 코드를 자세히 설명하겠습니다.

• X: 입력 데이터로서 리스트입니다. 이 리스트에는 모델의 여러 입력 특성이 포함되어 있습니다. 예를 들어, 이미지 및 텍스트 입력을 모두 처리하는 모델의 경우 X는 [image_data, text_data]와 같은 형식이 될 수 있습니다.
• y: 레이블 데이터입니다. 입력 데이터와 대응하는 정답 레이블을 나타내는 텐서 또는 배열입니다.
• devices: 데이터를 분할할 디바이스의 리스트입니다. 딥러닝 모델을 병렬로 실행하려는 디바이스 목록입니다. 예를 들어, GPU가 두 개인 경우 devices는 [gpu(0), gpu(1)]과 같은 형식일 수 있습니다.

이 함수의 목적은 X와 y를 여러 디바이스에 분할하는 것입니다. 각 디바이스에는 데이터 일부가 할당됩니다. 이를 통해 모델의 순전파 및 역전파 과정을 병렬로 수행하여 훈련 속도를 높일 수 있습니다.

구체적으로 함수의 동작은 다음과 같습니다.

1. zip(*[gluon.utils.split_and_load(feature, devices, even_split=False) for feature in X]): 입력 특성 X를 여러 디바이스에 분할합니다. split_and_load 함수는 입력 데이터를 주어진 디바이스에 분할하여 반환합니다. even_split=False로 설정되어 있으므로 데이터가 불균형하게 분할될 수 있습니다.
2. gluon.utils.split_and_load(y, devices, even_split=False): 레이블 데이터 y를 여러 디바이스에 분할합니다. 이것도 split_and_load 함수를 사용하여 수행됩니다.
3. 결과는 (X, y) 튜플로 반환됩니다. X는 입력 특성의 리스트이며, 각 리스트 요소는 하나의 디바이스에 할당된 입력 데이터입니다. y는 레이블 데이터로서, 각 디바이스에 할당된 레이블입니다.

이렇게 분할된 데이터는 각 디바이스에서 모델을 독립적으로 실행할 수 있게 하며, 그렇게 함으로써 모델의 훈련을 가속화할 수 있습니다.

Now we can train and evaluate the model on the SNLI dataset.

이제 SNLI 데이터 세트에서 모델을 훈련하고 평가할 수 있습니다.

lr, num_epochs = 0.001, 4
trainer = torch.optim.Adam(net.parameters(), lr=lr)
loss = nn.CrossEntropyLoss(reduction="none")
d2l.train_ch13(net, train_iter, test_iter, loss, trainer, num_epochs, devices)

이 코드는 모델을 훈련하는 데 필요한 하이퍼파라미터 설정과 훈련 프로세스를 실행하는 부분입니다.

• lr: 학습률(learning rate)로, 모델의 가중치 업데이트에 사용되는 스케일 파라미터입니다. 이 경우 학습률은 0.001로 설정됩니다.
• num_epochs: 에폭 수로, 전체 훈련 데이터셋을 몇 번 반복하여 학습할 것인지를 결정합니다. 이 경우 4번의 에폭으로 설정됩니다.
• trainer: 옵티마이저로, 모델의 가중치를 업데이트하는 데 사용됩니다. 여기서는 Adam 옵티마이저를 사용하며, 학습률은 위에서 설정한 lr 값을 사용합니다. net.parameters()를 통해 모델의 학습 가능한 가중치를 전달합니다.
• loss: 손실 함수로, 모델의 성능을 평가하고 손실을 최소화하기 위해 역전파(backpropagation) 과정에서 사용됩니다. 이 경우 크로스 엔트로피 손실 함수를 사용하며, reduction="none"으로 설정하여 각 미니배치의 개별 예제에 대한 손실을 계산합니다.
• d2l.train_ch13(net, train_iter, test_iter, loss, trainer, num_epochs, devices): 모델을 훈련하는 함수인 train_ch13를 호출합니다. 이 함수는 주어진 모델(net), 훈련 데이터셋(train_iter), 테스트 데이터셋(test_iter), 손실 함수(loss), 옵티마이저(trainer), 에폭 수(num_epochs), 그리고 디바이스(devices)에 따라 모델을 학습하고 테스트합니다.

이 코드는 모델을 설정하고 학습을 진행하는 부분으로, 주어진 하이퍼파라미터와 데이터셋으로 모델을 훈련합니다.

loss 0.496, train acc 0.805, test acc 0.828
20383.2 examples/sec on [device(type='cuda', index=0), device(type='cuda', index=1)]

16.5.2.4. Using the Model

Finally, define the prediction function to output the logical relationship between a pair of premise and hypothesis.

마지막으로 전제 premise 와 가설 hypothesis 쌍의 논리적 관계를 출력하는 예측 함수를 정의합니다.

#@save
def predict_snli(net, vocab, premise, hypothesis):
    """Predict the logical relationship between the premise and hypothesis."""
    net.eval()
    premise = torch.tensor(vocab[premise], device=d2l.try_gpu())
    hypothesis = torch.tensor(vocab[hypothesis], device=d2l.try_gpu())
    label = torch.argmax(net([premise.reshape((1, -1)),
                           hypothesis.reshape((1, -1))]), dim=1)
    return 'entailment' if label == 0 else 'contradiction' if label == 1 \
            else 'neutral'

이 코드는 학습된 모델을 사용하여 주어진 전제(premise)와 가설(hypothesis) 사이의 논리적 관계를 예측하는 함수인 predict_snli를 정의합니다. 이 함수는 다음과 같은 작업을 수행합니다:

• net.eval(): 모델을 평가 모드로 설정합니다. 이것은 모델이 평가 모드에서 동작하도록 하며, 드롭아웃(dropout) 및 배치 정규화(batch normalization)와 같은 학습 중에만 필요한 연산들을 비활성화합니다.
• premise와 hypothesis: 전제와 가설은 텍스트 형식으로 주어지며, 이를 모델의 입력 형식에 맞게 변환합니다. 우선 vocab을 사용하여 텍스트를 토큰으로 변환하고, 그 다음에는 torch.tensor를 사용하여 텐서 형식으로 변환합니다. 이때, d2l.try_gpu()를 사용하여 가능한 경우 GPU 디바이스에 텐서를 할당합니다.
• net([premise.reshape((1, -1)), hypothesis.reshape((1, -1))]): 모델에 입력 데이터를 전달하여 논리적 관계를 예측합니다. 입력은 전제와 가설을 포함하며, 모델의 입력 형식에 맞게 텐서를 조작하고 모델에 전달합니다.
• label = torch.argmax(...): 모델의 출력에서 가장 높은 확률을 가지는 클래스를 선택합니다. 이를 위해 torch.argmax 함수를 사용하고, dim=1을 설정하여 각 예제에 대한 예측 클래스를 선택합니다.
• 최종적으로 예측된 클래스에 따라 'entailment' (유추), 'contradiction' (모순), 또는 'neutral' (중립) 중 하나의 논리적 관계를 반환합니다.

이 함수를 사용하면 모델을 통해 주어진 전제와 가설의 논리적 관계를 예측할 수 있습니다.

We can use the trained model to obtain the natural language inference result for a sample pair of sentences.

훈련된 모델을 사용하여 샘플 문장 쌍에 대한 자연어 추론 결과를 얻을 수 있습니다.

predict_snli(net, vocab, ['he', 'is', 'good', '.'], ['he', 'is', 'bad', '.'])

이 코드는 predict_snli 함수를 사용하여 두 개의 문장(전제와 가설) 사이의 논리적 관계를 예측하는 예제입니다.

• net: 미리 학습된 모델로, 두 문장 사이의 논리적 관계를 예측하는 역할을 합니다.
• vocab: 어휘 사전으로, 모델이 텍스트를 이해하고 처리하는 데 사용됩니다.
• ['he', 'is', 'good', '.']: 첫 번째 문장인 전제를 토큰화한 리스트입니다. 여기서는 "he", "is", "good", "."로 구성되어 있습니다.
• ['he', 'is', 'bad', '.']: 두 번째 문장인 가설을 토큰화한 리스트입니다. 여기서는 "he", "is", "bad", "."로 구성되어 있습니다.

predict_snli 함수는 이 두 문장을 입력으로 받아 모델을 사용하여 논리적 관계를 예측하고, 예측된 결과를 반환합니다. 예를 들어, 이 코드를 실행하면 전제와 가설 사이의 관계를 예측하여 "entailment" (유추) 또는 "contradiction" (모순) 또는 "neutral" (중립) 중 하나의 결과를 반환할 것입니다.

'contradiction'

16.5.3. Summary

• The decomposable attention model consists of three steps for predicting the logical relationships between premises and hypotheses: attending, comparing, and aggregating.
  
  분해 가능한 주의 모델은 전제와 가설 사이의 논리적 관계를 예측하기 위한 세 가지 단계(참석, 비교, 집계)로 구성됩니다.
  
  
• With attention mechanisms, we can align tokens in one text sequence to every token in the other, and vice versa. Such alignment is soft using weighted average, where ideally large weights are associated with the tokens to be aligned.
  
  주의 메커니즘을 사용하면 한 텍스트 시퀀스의 토큰을 다른 텍스트 시퀀스의 모든 토큰에 정렬하거나 그 반대로 정렬할 수 있습니다. 이러한 정렬은 가중 평균을 사용하여 소프트하게 이루어지며, 이상적으로는 큰 가중치가 정렬할 토큰과 연결됩니다.
  
  
• The decomposition trick leads to a more desirable linear complexity than quadratic complexity when computing attention weights.
  
  분해 트릭은 주의 가중치를 계산할 때 2차 복잡도보다 더 바람직한 선형 복잡도로 이어집니다.
  
  
• We can use pretrained word vectors as the input representation for downstream natural language processing task such as natural language inference.
  
  자연어 추론과 같은 다운스트림 자연어 처리 작업을 위한 입력 표현으로 사전 훈련된 단어 벡터를 사용할 수 있습니다.

16.5.4. Exercises

1. Train the model with other combinations of hyperparameters. Can you get better accuracy on the test set?
2. What are major drawbacks of the decomposable attention model for natural language inference?
3. Suppose that we want to get the level of semantical similarity (e.g., a continuous value between 0 and 1) for any pair of sentences. How shall we collect and label the dataset? Can you design a model with attention mechanisms?

16.4. Natural Language Inference and the Dataset — Dive into Deep Learning 1.0.3 documentation (d2l.ai)

16.4. Natural Language Inference and the Dataset

In Section 16.1, we discussed the problem of sentiment analysis. This task aims to classify a single text sequence into predefined categories, such as a set of sentiment polarities. However, when there is a need to decide whether one sentence can be inferred form another, or eliminate redundancy by identifying sentences that are semantically equivalent, knowing how to classify one text sequence is insufficient. Instead, we need to be able to reason over pairs of text sequences.

섹션 16.1에서 우리는 감정 분석의 문제를 논의했습니다. 이 작업의 목표는 단일 텍스트 시퀀스를 감정 극성 세트 set of sentiment polarities와 같은 사전 정의된 카테고리로 분류하는 것입니다. 그러나 한 문장이 다른 문장에서 추론될 수 있는지 여부를 결정하거나 의미상 동일한 문장을 식별하여 중복을 제거해야 하는 경우 하나의 텍스트 시퀀스를 분류하는 방법을 아는 것만으로는 충분하지 않습니다. 대신, 텍스트 시퀀스 쌍을 추론할 수 있어야 합니다.

16.4.1. Natural Language Inference

Natural language inference studies whether a hypothesis can be inferred from a premise, where both are a text sequence. In other words, natural language inference determines the logical relationship between a pair of text sequences. Such relationships usually fall into three types:

자연어 추론은 둘 다 텍스트 시퀀스인 전제로부터 가설을 추론할 수 있는지 여부를 연구합니다. 즉, 자연어 추론은 한 쌍의 텍스트 시퀀스 간의 논리적 관계를 결정합니다. 이러한 관계는 일반적으로 세 가지 유형으로 나뉩니다.

• Entailment: the hypothesis can be inferred from the premise.
  
  수반: 전제로부터 가설을 추론할 수 있습니다.
  
  
• Contradiction: the negation of the hypothesis can be inferred from the premise.
  
  모순: 가설의 부정은 전제로부터 추론될 수 있습니다.
  
  
• Neutral: all the other cases.
  
  중립: 다른 모든 경우.

Natural language inference is also known as the recognizing textual entailment task. For example, the following pair will be labeled as entailment because “showing affection” in the hypothesis can be inferred from “hugging one another” in the premise.

자연어 추론은 텍스트 수반 작업 인식으로도 알려져 있습니다. 예를 들어, 가설의 "애정 표시"가 전제의 "서로 포옹"에서 추론될 수 있기 때문에 다음 쌍은 수반으로 분류됩니다.

Premise (전제): Two women are hugging each other.

Hypothesis (가설): Two women are showing affection.

The following is an example of contradiction as “running the coding example” indicates “not sleeping” rather than “sleeping”.

다음은 "코딩 예제를 실행하는 것"이 "자고 있음"이 아닌 "자지 않음"을 의미하므로 모순의 예입니다.

Premise: A man is running the coding example from Dive into Deep Learning.

Hypothesis: The man is sleeping.

The third example shows a neutrality relationship because neither “famous” nor “not famous” can be inferred from the fact that “are performing for us”.

세 번째 예는 '우리를 위해 공연하고 있다'는 사실에서 '유명하다'도 '유명하지 않다'도 추론할 수 없기 때문에 중립 관계를 보여준다.

Premise: The musicians are performing for us.

Hypothesis: The musicians are famous.

Natural language inference has been a central topic for understanding natural language. It enjoys wide applications ranging from information retrieval to open-domain question answering. To study this problem, we will begin by investigating a popular natural language inference benchmark dataset.

자연어 추론은 자연어를 이해하기 위한 핵심 주제였습니다. 정보 검색부터 오픈 도메인 질문 응답까지 폭넓게 응용됩니다. 이 문제를 연구하기 위해 먼저 인기 있는 자연어 추론 벤치마크 데이터 세트를 조사하겠습니다.

16.4.2. The Stanford Natural Language Inference (SNLI) Dataset

Stanford Natural Language Inference (SNLI) Corpus is a collection of over 500000 labeled English sentence pairs (Bowman et al., 2015). We download and store the extracted SNLI dataset in the path ../data/snli_1.0.

SNLI(Stanford Natural Language Inference) 코퍼스는 500,000개가 넘는 레이블이 있는 영어 문장 쌍의 모음입니다(Bowman et al., 2015). 추출된 SNLI 데이터 세트를 다운로드하여 ../data/snli_1.0 경로에 저장합니다.

import os
import re
import torch
from torch import nn
from d2l import torch as d2l

#@save
d2l.DATA_HUB['SNLI'] = (
    'https://nlp.stanford.edu/projects/snli/snli_1.0.zip',
    '9fcde07509c7e87ec61c640c1b2753d9041758e4')

data_dir = d2l.download_extract('SNLI')

이 코드는 SNLI 데이터셋을 다운로드하고 압축을 해제하는 파이토치 코드입니다. 코드의 작동 방식을 설명하겠습니다.

1. 필요한 라이브러리 및 모듈 임포트:
   • import os: 파일 및 디렉터리 경로를 조작하기 위한 파이썬 기본 모듈입니다.
   • import re: 정규 표현식을 활용하기 위한 모듈입니다.
   • import torch: 파이토치 라이브러리입니다.
   • from torch import nn: 파이토치의 신경망 모듈을 임포트합니다.
   • from d2l import torch as d2l: 'd2l' 모듈에서 'torch' 모듈을 임포트하고, 'd2l'이라는 이름으로 사용합니다.
2. 데이터셋 정보 설정:
   • d2l.DATA_HUB['SNLI']: SNLI 데이터셋에 대한 정보를 딕셔너리로 지정합니다. 데이터셋의 URL과 파일 해시값을 포함합니다.
   • data_dir = d2l.download_extract('SNLI'): 'd2l' 라이브러리의 download_extract 함수를 사용하여 SNLI 데이터셋을 다운로드하고 압축을 해제합니다. 데이터셋의 압축이 해제된 경로를 data_dir 변수에 저장합니다.

결과적으로, 이 코드는 SNLI 데이터셋을 다운로드하고 압축을 해제하여 사용할 준비를 하는 과정을 수행합니다. 이 데이터셋은 자연어 처리 작업에서 활용되며, 모델 학습 및 평가에 사용될 수 있습니다.

16.4.2.1. Reading the Dataset

The original SNLI dataset contains much richer information than what we really need in our experiments. Thus, we define a function read_snli to only extract part of the dataset, then return lists of premises, hypotheses, and their labels.

원본 SNLI 데이터 세트에는 실험에 실제로 필요한 것보다 훨씬 더 풍부한 정보가 포함되어 있습니다. 따라서 우리는 데이터 세트의 일부만 추출한 다음 전제, 가설 및 해당 레이블 목록을 반환하도록 read_snli 함수를 정의합니다.

#@save
def read_snli(data_dir, is_train):
    """Read the SNLI dataset into premises, hypotheses, and labels."""
    def extract_text(s):
        # Remove information that will not be used by us
        s = re.sub('\\(', '', s)
        s = re.sub('\\)', '', s)
        # Substitute two or more consecutive whitespace with space
        s = re.sub('\\s{2,}', ' ', s)
        return s.strip()
    label_set = {'entailment': 0, 'contradiction': 1, 'neutral': 2}
    file_name = os.path.join(data_dir, 'snli_1.0_train.txt'
                             if is_train else 'snli_1.0_test.txt')
    with open(file_name, 'r') as f:
        rows = [row.split('\t') for row in f.readlines()[1:]]
    premises = [extract_text(row[1]) for row in rows if row[0] in label_set]
    hypotheses = [extract_text(row[2]) for row in rows if row[0] in label_set]
    labels = [label_set[row[0]] for row in rows if row[0] in label_set]
    return premises, hypotheses, labels

이 코드는 SNLI 데이터셋을 읽어와 문장 및 레이블을 추출하는 함수를 정의하는 파이토치 코드입니다. 코드의 작동 방식을 설명하겠습니다.

1. 함수 정의:
   • read_snli(data_dir, is_train): SNLI 데이터셋을 읽어와 문장과 레이블을 추출하는 함수입니다. data_dir은 데이터셋이 위치한 디렉터리 경로이고, is_train은 훈련 데이터인지 여부를 나타내는 변수입니다.
2. 문장 추출 및 전처리:
   • extract_text(s): 주어진 문자열 s를 전처리하는 함수입니다. 괄호 및 공백을 제거하고, 연속된 공백을 하나의 공백으로 대체한 후 양쪽 공백을 제거하여 문장을 정리합니다.
3. 레이블 설정:
   • label_set: 레이블과 해당하는 숫자를 매핑한 딕셔너리입니다.
4. 데이터 파일 읽기:
   • file_name: 데이터 파일 경로를 설정합니다. is_train에 따라 훈련 데이터 또는 테스트 데이터 파일을 선택합니다.
   • with open(file_name, 'r') as f:: 파일을 열고 읽기 모드로 처리합니다.
   • rows = [row.split('\t') for row in f.readlines()[1:]]: 파일에서 읽은 각 행을 탭으로 분리하여 리스트로 변환합니다. 첫 번째 행은 헤더이므로 무시합니다.
5. 문장 및 레이블 추출:
   • premises, hypotheses, labels: 각 행에서 필요한 정보를 추출하여 각각의 리스트에 저장합니다. 레이블은 label_set을 이용하여 숫자로 변환합니다.

결과적으로, 이 함수는 데이터 디렉터리에서 SNLI 데이터셋을 읽어와 전처리된 문장과 레이블을 추출하여 반환하는 역할을 수행합니다.

Now let’s print the first 3 pairs of premise and hypothesis, as well as their labels (“0”, “1”, and “2” correspond to “entailment”, “contradiction”, and “neutral”, respectively ).

이제 전제와 가설의 처음 3쌍과 해당 레이블("0", "1" 및 "2"는 각각 "수반", "모순" 및 "중립"에 해당)을 인쇄해 보겠습니다.

train_data = read_snli(data_dir, is_train=True)
for x0, x1, y in zip(train_data[0][:3], train_data[1][:3], train_data[2][:3]):
    print('premise:', x0)
    print('hypothesis:', x1)
    print('label:', y)

이 코드는 SNLI 데이터셋에서 훈련 데이터를 읽어와 문장과 레이블을 출력하는 작업을 수행하는 파이토치 코드입니다. 코드의 작동 방식을 설명하겠습니다.

1. 훈련 데이터 읽기:
   • train_data = read_snli(data_dir, is_train=True): read_snli 함수를 사용하여 훈련 데이터를 읽어옵니다. 이 함수는 premises, hypotheses, labels를 반환합니다.
2. 데이터 출력:
   • for x0, x1, y in zip(train_data[0][:3], train_data[1][:3], train_data[2][:3]):: 훈련 데이터에서 처음 3개의 데이터에 대해서 반복문을 실행합니다. x0는 premises, x1은 hypotheses, y는 labels를 나타냅니다.
   • print('premise:', x0): 현재 반복에서 추출한 premises를 출력합니다.
   • print('hypothesis:', x1): 현재 반복에서 추출한 hypotheses를 출력합니다.
   • print('label:', y): 현재 반복에서 추출한 label을 출력합니다.

결과적으로, 이 코드는 훈련 데이터에서 처음 3개의 문장과 해당하는 가설, 레이블을 출력하여 데이터가 올바르게 읽혔는지 확인하는 역할을 수행합니다.

premise: A person on a horse jumps over a broken down airplane .
hypothesis: A person is training his horse for a competition .
label: 2
premise: A person on a horse jumps over a broken down airplane .
hypothesis: A person is at a diner , ordering an omelette .
label: 1
premise: A person on a horse jumps over a broken down airplane .
hypothesis: A person is outdoors , on a horse .
label: 0

The training set has about 550000 pairs, and the testing set has about 10000 pairs. The following shows that the three labels “entailment”, “contradiction”, and “neutral” are balanced in both the training set and the testing set.

훈련 세트에는 약 550000개의 쌍이 있고 테스트 세트에는 약 10000개의 쌍이 있습니다. 다음은 "수반", "모순" 및 "중립"이라는 세 가지 레이블이 훈련 세트와 테스트 세트 모두에서 균형을 이루고 있음을 보여줍니다.

test_data = read_snli(data_dir, is_train=False)
for data in [train_data, test_data]:
    print([[row for row in data[2]].count(i) for i in range(3)])

이 코드는 SNLI 데이터셋에서 훈련 데이터와 테스트 데이터의 레이블 분포를 출력하는 작업을 수행하는 파이토치 코드입니다. 코드의 작동 방식을 설명하겠습니다.

1. 테스트 데이터 읽기:
   • test_data = read_snli(data_dir, is_train=False): read_snli 함수를 사용하여 테스트 데이터를 읽어옵니다. 이 함수는 premises, hypotheses, labels를 반환합니다. is_train을 False로 설정하여 테스트 데이터를 가져옵니다.
2. 레이블 분포 출력:
   • for data in [train_data, test_data]:: 훈련 데이터와 테스트 데이터에 대해 각각 반복문을 실행합니다.
   • print([[row for row in data[2]].count(i) for i in range(3)]): 각 데이터의 레이블 분포를 출력합니다. 각 레이블(0, 1, 2)별로 데이터에서 해당 레이블의 개수를 계산하여 출력합니다.

결과적으로, 이 코드는 훈련 데이터와 테스트 데이터에서 각 레이블(0, 1, 2)별로 데이터의 분포를 출력하여 어떤 레이블이 얼마나 많은지를 확인하는 역할을 수행합니다.

[183416, 183187, 182764]
[3368, 3237, 3219]

16.4.2.2. Defining a Class for Loading the Dataset

Below we define a class for loading the SNLI dataset by inheriting from the Dataset class in Gluon. The argument num_steps in the class constructor specifies the length of a text sequence so that each minibatch of sequences will have the same shape. In other words, tokens after the first num_steps ones in longer sequence are trimmed, while special tokens “<pad>” will be appended to shorter sequences until their length becomes num_steps. By implementing the __getitem__ function, we can arbitrarily access the premise, hypothesis, and label with the index idx.

아래에서는 Gluon의 Dataset 클래스를 상속하여 SNLI 데이터 세트를 로드하기 위한 클래스를 정의합니다. 클래스 생성자의 num_steps 인수는 각 시퀀스 미니 배치가 동일한 모양을 갖도록 텍스트 시퀀스의 길이를 지정합니다. 즉, 긴 시퀀스에서 첫 번째 num_steps 이후의 토큰은 잘리는 반면, 특수 토큰 "<pad>"는 길이가 num_steps가 될 때까지 더 짧은 시퀀스에 추가됩니다. __getitem__ 함수를 구현하면 인덱스 idx로 전제, 가설, 레이블에 임의로 접근할 수 있습니다.

#@save
class SNLIDataset(torch.utils.data.Dataset):
    """A customized dataset to load the SNLI dataset."""
    def __init__(self, dataset, num_steps, vocab=None):
        self.num_steps = num_steps
        all_premise_tokens = d2l.tokenize(dataset[0])
        all_hypothesis_tokens = d2l.tokenize(dataset[1])
        if vocab is None:
            self.vocab = d2l.Vocab(all_premise_tokens + all_hypothesis_tokens,
                                   min_freq=5, reserved_tokens=['<pad>'])
        else:
            self.vocab = vocab
        self.premises = self._pad(all_premise_tokens)
        self.hypotheses = self._pad(all_hypothesis_tokens)
        self.labels = torch.tensor(dataset[2])
        print('read ' + str(len(self.premises)) + ' examples')

    def _pad(self, lines):
        return torch.tensor([d2l.truncate_pad(
            self.vocab[line], self.num_steps, self.vocab['<pad>'])
                         for line in lines])

    def __getitem__(self, idx):
        return (self.premises[idx], self.hypotheses[idx]), self.labels[idx]

    def __len__(self):
        return len(self.premises)

위의 코드는 SNLI(Sentence Natural Language Inference) 데이터셋을 로드하기 위한 사용자 정의 데이터셋 클래스인 SNLIDataset을 정의하는 부분입니다. 이 클래스는 PyTorch의 torch.utils.data.Dataset 클래스를 상속하여 구현되었습니다.

이 클래스의 주요 목적은 SNLI 데이터를 모델에 입력으로 공급하기 위한 데이터 파이프라인을 구축하는 것입니다. 이 데이터셋은 주어진 문장 쌍(전제문과 가설문)에 대한 텍스트와 해당 라벨(문장 간의 관계)을 처리합니다.

클래스 내부에서 다음 주요 구성 요소를 확인할 수 있습니다.

• __init__: 데이터셋의 초기화 함수입니다. 이 함수는 다음 인자들을 받습니다.
  • dataset: 데이터셋으로부터 읽은 원시 데이터 (전제문, 가설문, 라벨)입니다.
  • num_steps: 데이터의 시퀀스 길이를 지정하는 인자로, 긴 시퀀스를 자르거나 패딩하는 데 사용됩니다.
  • vocab: 선택적으로 전달되는 어휘 사전입니다. 어휘 사전을 직접 제공하지 않으면, 데이터셋에서 자동으로 어휘 사전을 생성합니다.
• _pad: 시퀀스를 주어진 num_steps 길이로 패딩하고 어휘 사전에 맞게 인덱스로 변환하는 내부 함수입니다.
• __getitem__: 데이터셋에서 데이터를 로드할 때 호출되는 함수로, 주어진 인덱스 idx에 해당하는 전제문과 가설문, 그리고 라벨을 반환합니다.
• __len__: 데이터셋의 전체 샘플 수를 반환하는 함수입니다.

SNLIDataset 클래스를 사용하면 SNLI 데이터셋을 쉽게 PyTorch 데이터로 변환하고 데이터 로더를 통해 모델에 공급할 수 있습니다

16.4.2.3. Putting It All Together

Now we can invoke the read_snli function and the SNLIDataset class to download the SNLI dataset and return DataLoader instances for both training and testing sets, together with the vocabulary of the training set. It is noteworthy that we must use the vocabulary constructed from the training set as that of the testing set. As a result, any new token from the testing set will be unknown to the model trained on the training set.

이제 read_snli 함수와 SNLIDataset 클래스를 호출하여 SNLI 데이터 세트를 다운로드하고 훈련 세트의 어휘와 함께 훈련 세트와 테스트 세트 모두에 대한 DataLoader 인스턴스를 반환할 수 있습니다. 훈련 세트에서 구성된 어휘를 테스트 세트의 어휘로 사용해야 한다는 점은 주목할 만합니다. 결과적으로 테스트 세트의 새로운 토큰은 훈련 세트에서 훈련된 모델에 알려지지 않습니다.

#@save
def load_data_snli(batch_size, num_steps=50):
    """Download the SNLI dataset and return data iterators and vocabulary."""
    num_workers = d2l.get_dataloader_workers()
    data_dir = d2l.download_extract('SNLI')
    train_data = read_snli(data_dir, True)
    test_data = read_snli(data_dir, False)
    train_set = SNLIDataset(train_data, num_steps)
    test_set = SNLIDataset(test_data, num_steps, train_set.vocab)
    train_iter = torch.utils.data.DataLoader(train_set, batch_size,
                                             shuffle=True,
                                             num_workers=num_workers)
    test_iter = torch.utils.data.DataLoader(test_set, batch_size,
                                            shuffle=False,
                                            num_workers=num_workers)
    return train_iter, test_iter, train_set.vocab

위의 코드는 SNLI(Sentence Natural Language Inference) 데이터셋을 다운로드하고 데이터 반복자(data iterators)와 어휘 사전(vocabulary)을 반환하는 함수인 load_data_snli를 정의한 부분입니다. 이 함수를 통해 데이터를 준비하고 모델에 공급할 수 있는 형태로 만듭니다.

주요 구성 요소와 작업 단계는 다음과 같습니다.

• num_workers: 데이터 로더에 사용할 병렬 작업자 수를 결정하는 변수입니다.
• data_dir: 데이터셋 파일이 저장될 디렉토리를 지정하는 변수입니다.
• train_data와 test_data: read_snli 함수를 사용하여 SNLI 데이터셋을 읽어온 원시 데이터입니다.
• train_set과 test_set: SNLIDataset 클래스를 사용하여 데이터를 전처리하고 PyTorch 데이터셋 형식으로 변환한 데이터셋입니다. 각 데이터셋에는 전제문과 가설문의 시퀀스, 그리고 문장 간의 관계를 나타내는 라벨이 포함되어 있습니다.
• train_iter와 test_iter: torch.utils.data.DataLoader를 사용하여 배치(batch) 단위로 데이터를 불러오는 데이터 반복자입니다. 이 반복자들은 모델 학습 및 평가에 사용됩니다.
• train_set.vocab: 데이터셋의 어휘 사전입니다. 이 어휘 사전은 전체 데이터셋의 어휘를 관리하며, 텍스트 데이터를 숫자로 변환하는 데 사용됩니다.

이 함수를 호출하면 학습용(train_iter)과 테스트용(test_iter) 데이터 반복자와 어휘 사전(train_set.vocab)이 반환됩니다. 이러한 데이터 반복자와 어휘 사전을 사용하여 모델 학습 및 평가를 수행할 수 있습니다.

Here we set the batch size to 128 and sequence length to 50, and invoke the load_data_snli function to get the data iterators and vocabulary. Then we print the vocabulary size.

여기서는 배치 크기를 128로 설정하고 시퀀스 길이를 50으로 설정하고 load_data_snli 함수를 호출하여 데이터 반복자와 어휘를 가져옵니다. 그런 다음 어휘 크기를 인쇄합니다.

train_iter, test_iter, vocab = load_data_snli(128, 50)
len(vocab)

이 코드는 SNLI 데이터셋을 로드하여 데이터 반복자(train_iter, test_iter)와 어휘 사전(vocab)을 생성하고, 어휘 사전의 크기를 출력하는 작업을 수행하는 파이토치 코드입니다. 코드의 작동 방식을 설명하겠습니다.

1. 데이터 로드 및 어휘 생성:
   • train_iter, test_iter, vocab = load_data_snli(128, 50): load_data_snli 함수를 사용하여 SNLI 데이터셋을 로드하고 데이터 반복자(train_iter, test_iter)와 어휘 사전(vocab)을 생성합니다. 인자로 배치 크기(128)와 문장의 최대 토큰 개수(50)를 전달합니다.
2. 어휘 사전 크기 출력:
   • len(vocab): 생성된 어휘 사전의 크기를 출력합니다. 이 값은 어휘 사전에 등록된 고유한 단어의 개수를 나타냅니다.

결과적으로, 이 코드는 SNLI 데이터셋을 로드하고 어휘 사전을 생성한 후, 생성된 어휘 사전의 크기를 출력하여 데이터 처리 과정의 결과를 확인하는 역할을 수행합니다.

read 549367 examples
read 9824 examples

18678

Now we print the shape of the first minibatch. Contrary to sentiment analysis, we have two inputs X[0] and X[1] representing pairs of premises and hypotheses.

이제 첫 번째 미니배치의 모양을 인쇄합니다. 감정 분석과 달리 전제와 가설의 쌍을 나타내는 두 개의 입력 X[0] 및 X[1]이 있습니다.

for X, Y in train_iter:
    print(X[0].shape)
    print(X[1].shape)
    print(Y.shape)
    break

위의 코드는 학습 데이터 반복자(train_iter)를 통해 첫 번째 미니배치(mini-batch) 데이터를 가져와서 각 구성 요소의 모양(shape)을 출력하는 부분입니다. 이 코드를 통해 데이터의 형태를 이해할 수 있습니다.

• for X, Y in train_iter:: 학습 데이터 반복자인 train_iter를 순회하며 각 미니배치를 가져옵니다. X는 입력 데이터, Y는 해당 입력에 대한 라벨(정답)을 나타냅니다.
• print(X[0].shape): 현재 미니배치의 첫 번째 요소 X[0]의 모양(shape)을 출력합니다. 여기서 X[0]은 입력 데이터 중 첫 번째 시퀀스에 해당합니다.
• print(X[1].shape): 현재 미니배치의 두 번째 요소 X[1]의 모양(shape)을 출력합니다. X[1]은 입력 데이터 중 두 번째 시퀀스에 해당합니다.
• print(Y.shape): 현재 미니배치의 라벨(정답) 데이터 Y의 모양(shape)을 출력합니다.
• break: 첫 번째 미니배치의 출력 후에 반복문을 종료합니다. 이 부분은 미니배치의 구성 요소를 확인하기 위한 간단한 디버깅 용도로 사용됩니다.

이 코드를 실행하면 첫 번째 미니배치의 입력 데이터와 라벨의 모양을 확인할 수 있으며, 이를 통해 모델을 설계할 때 입력 및 출력의 형태를 정확하게 지정하는 데 도움이 됩니다.

torch.Size([128, 50])
torch.Size([128, 50])
torch.Size([128])

16.4.3. Summary

• Natural language inference studies whether a hypothesis can be inferred from a premise, where both are a text sequence.
  
  자연어 추론은 둘 다 텍스트 시퀀스인 전제로부터 가설을 추론할 수 있는지 여부를 연구합니다.
  
  
• In natural language inference, relationships between premises and hypotheses include entailment, contradiction, and neutral.
  
  자연어 추론에서 전제와 가설 사이의 관계에는 수반, 모순, 중립이 포함됩니다.
  
  
• Stanford Natural Language Inference (SNLI) Corpus is a popular benchmark dataset of natural language inference.
  
  SNLI(Stanford Natural Language Inference) 코퍼스는 자연어 추론에 대한 인기 있는 벤치마크 데이터세트입니다.
  
  

16.4.4. Exercises

1. Machine translation has long been evaluated based on superficial n-gram matching between an output translation and a ground-truth translation. Can you design a measure for evaluating machine translation results by using natural language inference?
2. How can we change hyperparameters to reduce the vocabulary size?